Théorie de la perturbation
En mécanique quantique, la théorie de la perturbation est un ensemble de schémas d'approximations liée à une perturbation mathématique utilisée pour décrire un dispositif quantique complexe de façon simplifiée.
Recherche sur Google Images :
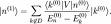
Source image : fr.wikipedia.org Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- ... La théorie de la perturbation échoue aussi à décrire des états générés.... Afin d'obtenir la correction du premier ordre de l'état propre... (source : scholar.google)
- représente, sous sa forme particulièrement générale, l'énergie des états... indépendante du temps et E l'énergie propre (eigenvalue) correspondant à la.... de AB ; A perturbe B et B perturbe A. La théorie des perturbations des orbitales... (source : scgc.epfl)
En mécanique quantique, la théorie de la perturbation (ou théorie des perturbations) est un ensemble de schémas d'approximations liée à une perturbation mathématique utilisée pour décrire un dispositif quantique complexe de façon simplifiée. L'idée est de partir d'un dispositif simple et d'appliquer graduellement un hamiltonien «perturbant» qui représente un écart léger comparé à l'équilibre du dispositif (perturbation). Si la perturbation n'est pas trop importante, les différentes quantités physiques associées avec le dispositif perturbé (comme ses niveaux d'énergie et états propres) seront générés de manière continue à partir de ceux du dispositif simple. On peut par conséquent donc étudier le premier à partir des connaissances sur le dernier.
Application de la théorie de la perturbation
La théorie de la perturbation est un outil important pour la description des dispositifs quantiques réels, car trouver des solutions exactes à l'équation de Schrödinger pour des hamiltoniens de dispositifs même modérément complexes peut être particulièrement complexe. Les hamiltoniens pour lesquels on connait des solutions exactes, comme pour l'atome d'hydrogène, de l'oscillateur harmonique quantique et la particule dans une boîte, sont trop parfaitisés pour décrire de manière correcte la majorité des dispositifs. En utilisant la théorie de la perturbation, on peut utiliser les solutions connues de ces hamiltoniens simples pour générer des solutions pour une série de dispositifs plus complexes. Ainsi, en ajoutant un potentiel électrique perturbateur au modèle quantique de l'atome d'hydrogène, on peut calculer les déplacements faibles des raies spectrales de l'hydrogène à cause de la présence d'un champ électrique (effet Stark). Ceci est uniquement une approximation, la somme d'un potentiel coulombien avec un potentiel linéaire est instable quoique le temps tunnel (radioactivité) est particulièrement important. Cela montre que même pour un aprécisément des raies d'énergie spectrale, la théorie de la perturbation échoue à traduire entièrement le phénomène.
Les modifications de formules induites par l'introduction de la perturbation ne sont pas exactes, mias peuvent conduire à des résultats précis tant que le paramètre de développement α reste faible. Au-delà d'un certain ordre n˜1 / α, cependant, les résultats deviennent divergents au fur et à mesure que les séries générées divergent, leur développement étant asymptotique. Il existe des manières de les convertir en séries convergentes, ce qui peut être reconnu pour des paramètres de développement importants, surtout par une méthode de perturbation variationnelle.
En électrodynamique quantique (QED) dans laquelle l'interaction électron-phonon est traitée de manière perturbative, le calcul du moment magnétique électronique est en accord avec l'expérience jusqu'à 11 décimales. Dans cette théorie, mais aussi pour d'autre théories quantiques des champs, des techniques spécifiques de calcul connues sous le nom de diagrammes de Feynman sont employées pour effectuer une somme systématique des termes de séries puissance.
Dans certaines circonstances, la théorie de la perturbation est une approche invalide. Cela se produit quand le dispositif à décrire ne peut être approché par une petite perturbation imposée à un dispositif simple. En chromodynamique quantique, par exemple, l'interaction des quarks avec le champ gluonique ne peut être traité par perturbation aux faibles énergies car la constante de couplage (paramètre de développement) devient trop important. La théorie de la perturbation échoue aussi à décrire des états générés de manière diabatique à partir du «modèle libre», comme les états liants et différents phénomènes collectifs comme les solitons. On considère généralement, par exemple, un dispositif de particules libres (non-interagissantes), dans lequel une interaction attractive est introduite. Selon la forme de cette interaction, un ensemble entièrement nouveau d'états propres correspondant aux groupes de particules liées à d'autres peut être créé. Un exemple de ce phénomène peut être trouvé en supraconductivité conventionnelle, dans laquelle l'attraction portée par les phonons entre les électrons de conduction mène à la formation de paires d'électrons corrélés connues sous le nom de paires de Cooper. Quand on a à faire à de tels dispositifs, on utilise généralement d'autres schémas d'approximation, comme la méthode variationnelle ou l'approximation BKW. En effet, il n'existe pas d'analogue à une particule liante dans le modèle non perturbé et l'énergie d'un soliton fluctue typiquement comme l'inverse du paramètre de développement. Cependant, si on «intègre» sur le phénomène solitonique, les corrections non perturbatives seront dans ce cas faibles, de l'ordre de e − 1 / g ou 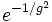 dans le paramètre de perturbation g. La théorie de la perturbation peut uniquement conduire à des solutions «proches» de la solution non-perturbée, même s'il existe d'autres solutions (qui augmentent typiquement lorsque le paramètre de développement approche de zéro).
dans le paramètre de perturbation g. La théorie de la perturbation peut uniquement conduire à des solutions «proches» de la solution non-perturbée, même s'il existe d'autres solutions (qui augmentent typiquement lorsque le paramètre de développement approche de zéro).
Le traitement des problèmes des dispositifs non-perturbatifs a été en partie aidé par l'essor des ordinateurs modernes. Il est devenu (assez) simple de trouver des solutions non-perturbatives pour certains problèmes, par le biais de méthodes comme la théorie de la fonctionnelle de la densité. Ces avancées ont spécifiquement profité à la chimie quantique. Les ordinateurs ont aussi été employés pour procéder à des calculs en principe de la perturbation atteignant de particulièrement hauts niveaux de précision, nécessaires et importants en physique des particules pour obtenir des résultats théoriques identiques à l'expérience.
Théorie de la perturbation indépendante du temps
Il y a deux catégories de théorie de la perturbation : indépendante du temps et dépendante du temps. Dans cette section, on traitera de la théorie de la perturbation indépendante du temps, dans laquelle le hamiltonien de perturbation est statique. La théorie de la perturbation indépendante du temps fut présentée dans un article[1] d'Erwin Schrödinger de 1926, peu après qu'il eut énoncé ses théories en mécanique ondulatoire. Dans cet article, Erwin Schrödinger faisait référence à un travail antérieur de lord Rayleigh[2] qui étudia les vibrations harmoniques d'une corde perturbée par des petites inhomogénéités. C'est pourquoi cette théorie de la perturbation est quelquefois nommée théorie de la perturbation de Rayleigh-Schrödinger.
Corrections du premier ordre
On débute en utilisant un hamiltonien non perturbé H0, qui est aussi reconnu comme indépendant du temps. Il possède des niveaux d'énergie et états propres connus, déterminés par l'équation de Schrödinger indépendante du temps :
Pour simplifier, on postule que les énergies sont discrètes. Les exposants (0) indiquent que ces quantités sont associées au dispositif non perturbé.
On peut alors introduire une perturbation dans le hamiltonien. Soit V un hamiltonien représentant une petite perturbation physique, comme un potentiel énergétique produisant un champ externe (donc V est formellement un opérateur hermitique). Soit λ un paramètre sans dimension pouvant prendre pour valeur des valeurs allant continument de 0 (pas de perturbation) à 1 (perturbation totale). Le hamiltonien perturbé est :
- H = H0 + λV.
Les niveaux d'énergie et états propres du hamiltonien perturbé sont de nouveau donnés par l'équation de Schrödinger :
L'objectif est alors d'exprimer En et |n> en termes de niveaux d'énergie et d'états propres de l'ancien hamiltonien. Si la perturbation est suffisamment faible, on peut les écrire en séries entières de λ :
où
et
Quand λ = 0, on diminué les équations aux valeurs non perturbées, qui sont les premiers termes de chaque série. Quand la perturbation est faible, les niveaux d'énergie et les états propres ne devraient pas énormément différer de leurs valeurs non perturbées, et les termes devraient rapidement devenir plus petits au fur et à mesure que l'ordre augmente.
Si on introduit ces séries dans l'équation de Schrödinger, on obtient :
Le développement de cette équation et la comparaison des cœfficients de chaque puissance de λ conduit à un dispositif d'équations illimité. L'équation d'ordre 0 est tout simplement l'équation de Schrödinger pour des dispositifs non perturbés. L'équation au premier ordre est :
que on multiplie par
C'est tout simplement l'espérance du hamiltonien de perturbation quand le dispositif est dans l'état non perturbée. Ce résultat peut être interprété de la manière suivant : supposons qu'une perturbation soit appliquée, mais qu'on conserve le dispositif dans l'état quantique |n (0) >, qui est un état quantique valide quoique ne correspondant plus à un état propre de l'énergie. La perturbation fait que l'énergie moyenne de cet état croît de
Avant de calculer les corrections à l'état propre d'énergie, on doit définir la question de la normalisation. On peut supposer
Afin d'obtenir la correction du premier ordre de l'état propre d'énergie, on entre l'expression de la correction énergétique de premier ordre dans le résultat indiquant les cœfficients de premier ordre de λ montré ci-dessus. On utilise ensuite la résolution de l'identité,
où 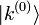 est le complément orthogonal de
est le complément orthogonal de 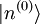 . Le résultat est :
. Le résultat est :
Supposons pour l'instant que le niveau d'énergie d'ordre zéro ne soit pas dégénéré, c'est-à-dire qu'il n'y ait pas d'état propre de H0 dans le complément orthogonal de 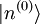 d'énergie
d'énergie 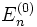 . On multiplie alors par <k (0) |, ce qui donne :
. On multiplie alors par <k (0) |, ce qui donne :
et donc le composant de la correction de premier ordre selon |k (0) > par le postulat 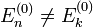 . Nous avons au total :
. Nous avons au total :
La modification de premier ordre dans le Nième ket propre de l'énergie possède une contribution des états propres de l'énergie k ≠ n. Chaque terme est proportionnel à l'élément de matrice
Corrections du deuxième ordre et suivants
On peut trouver les déviations d'ordres supérieurs par une méthode identique, quoique les calculs deviennent plus compliqués avec la formulation employée. La condition de normalisation indique que : 2
En étendant la méthode précédente, la correction d'énergie du troisième ordre peut être démontrée comme étant[3]
Effets de la dégénérescence
On suppose que deux ou plus états propres d'énergie sont dégénérés. Les calculs qui ont précédé pour les modifications d'énergie du premier ordre ne sont pas affectés, mais le calcul de la modification de l'état propre est problématique car l'opérateur
n'a pas d'inverse bien défini.
Cela relève d'un problème conceptuel plutôt que mathématique. Imaginons qu'on ait deux ou plus états propres perturbés avec différentes énergies, continument générés à partir d'un nombre identique d'états propres non perturbés dégénérés. Soit D le sous-espace occupé par ces états propres dégénérés. Le problème repose sur le fait qu'il n'y a pas de méthode unique pour choisir une base d'états propres de l'énergie pour un dispositif non perturbé. Surtout, on peut construire une base différente pour D en choisissant différentes combinaisons linéaires des états propres le constituant. Dans une telle base, les états propres non perturbés ne génèreraient pas continument les états propres perturbés.
On voit mais aussi, en présence d'une dégénérescence, la théorie de la perturbation ne fonctionne pas avec un choix de base arbitraire. On doit plutôt choisir une base telle que le hamiltonien de perturbation soit diagonal dans le sous-espace dégénéré D. En d'autres termes,
Dans ce cas, l'équation pour la perturbation de premier ordre dans l'état propre d'énergie se réduit à :
L'opérateur de gauche n'est pas singulier quand il est appliqué aux états propres n'appartenant pas à D, on peut alors écrire
Théorie de la perturbation dépendante du temps
La théorie de la perturbation dépendante du temps, développée par Paul Dirac, traite de l'effet d'une perturbation V (t) dépendante du temps appliquée à un hamiltonien H0 indépendant du temps. Le hamiltonien perturbé étant dépendant du temps, ses niveaux et états propres d'énergie le sont aussi. Donc, les objectifs de la théorie de la perturbation dépendante du temps sont un peu différents de ceux la théorie de la perturbation indépendante du temps. On traite les quantités suivantes :
- l'espérance mathématique dépendante du temps d'une observable A, pour un état d'origine donné.
- les amplitudes dépendantes du temps des états quantiques étant des kets propres (vecteurs propres) de l'énergie dans le dispositif non perturbé.
La première quantité est importante car elle est à l'origine du résultat classique d'une mesure de A réalisée sur un nombre macroscopique d'exemplaires du dispositif perturbé. A titre d'exemple, on peut prendre A comme le déplacement dans la direction x de l'électron dans un atome d'hydrogène, dans le cas duquel l'espérance mathématique, quand elle est multipliée par un cœfficient approprié, donne la polarisation électrique dépendante du temps du gaz d'hydrogène. Avec un choix approprié de perturbation (comme par exemple un potentiel électrique oscillant), cela sert à calculer la permittivité diélectrique du gaz.
La seconde concerne la probabilité temporelle d'occupation de chaque état propre. Cela est spécifiquement utile en physique des lasers, dans laquelle on s'intéresse à des populations dans différents états atomiques dans un gaz quand un champ électrique variable dans le temps est appliqué. Ces probabilités sont aussi utiles pour calculer l'élargissement quantique des raies spectrales.
On exposera brièvement ci-après les idées de la formulation de Dirac de la théorie de la perturbation dépendante du temps. Choisissons une base d'énergie {|n>} pour le dispositif non perturbé. On ne portera plus les exposants (0) pour les états propres, parler de niveaux d'énergie et d'états propres pour le dispositif perturbé étant peu significatif.
Si le dispositif non perturbé est un état propre |j> au temps t = 0, son état aux temps suivants fluctue uniquement d'une phase (on se place dans la représentation de Schrödinger, où les vecteurs d'état évoluent dans le temps et les opérateurs constants) :
On introduit alors un hamiltonien perturbé dépendant du temps V (t) . Le hamiltonien du dispositif perturbé est :
- H = H0 + V (t)
Soit |ψ (t) > la notation pour l'état quantique du dispositif perturbé au temps t. Il obéit à l'équation de Schrödinger dépendante du temps,
L'état quantique à chaque instant peut être exprimé comme une combinaison linéaire de la base propre {|n>}. On peut écrire la combinaison linéaire comme étant :
où les cn (t) sont des fonctions complexes non déterminées de t que nous appellerons amplitudes (à strictement parler, ce sont les amplitudes dans la représentation de Dirac). On a explicitement extrait les facteurs de phase exponentielle exp (-iEnt/h) du côté droit de l'équation. Cela est simplement un problème de convention, et peut être produit sans perte de la généralité. La raison pour laquelle on s'intéresse à ce problème est que lorsque le dispositif commence dans l'état |j> et qu'il n'y a pas de perturbation, les amplitudes ont la propriété intéressante que, pour tout t, cj (t) = 1 et cn (t) = 0 si n≠j.
Le carré de la valeur absolue de l'amplitude cn (t) est la probabilité que le dispositif soit dans l'état n au temps t :
Inséré dans l'équation de Schrödinger, et considérant ∂/∂t par dérivation des fonctions composées, on obtient :
En résolvant l'identité devant V, on peut diminuer cette équation en un ensemble d'équations aux dérivées partielles pour les amplitudes :
Les éléments de matrice de V jouent un rôle comparable à celui tenu dans la théorie de la perturbation indépendante du temps, étant proportionnels au taux auquel les amplitudes sont modifiées entre les états. Il faut noter, cependant, que la direction de la modification est conditionnée par le facteur de phase exponentiel. Sur des temps énormément plus importants que ceux correspondant à la différence d'énergie Ek-En, la phase peut cycler plusieurs fois. Si la dépendance en temps de V est suffisamment faible, cela peut provoquer une oscillation des amplitudes d'état. De telles oscillations sont utilisées pour gérer les transitions radiatives dans les lasers.
Jusque là, on n'a fait aucune approximation, par conséquent la totalité d'équations différentielles est exact. En indiquant des valeurs initiales appropriées cn (0), on peut habituellement trouver une solution exacte (non perturbative). Cela est aisément trouvé quand il y a uniquement deux niveaux d'énergie (n= 1, 2), et la solution est utile pour des dispositifs modèles comme la molécule d'ammoniaque. Cependant, il est complexe de trouver des solutions exactes quand il y a plusieurs niveaux d'énergie, et on cherchera plutôt des solutions perturbatives, qui peuvent être obtenues en mettant les équations sous une forme intégrale :
On effectuant de manière répétée la substitution pour chaque cn du côté droit, on obtient la solution itérative :
où, par exemple, le terme de premier ordre est :
De nombreux résultats induits peuvent être obtenus, comme la règle d'or de Fermi, qui lie le taux de transition entre états quantiques à la densité d'états à énergies spécifiques, et les séries de Dyson, obtenues en appliquant la méthode itérative à l'opérateur d'évolution temporelle, qui fait partie des points de départ de la méthode des diagrammes de Feynman. La Théorie de la perturbation de Møller-Plesset est une application de la théorie de la perturbation à la méthode Hartree-Fock.
Voir aussi
- règle d'or de Fermi
- théorie des perturbations
Références
Bibliographie
- Albert Messiah, Mécanique quantique [détail des éditions], chapitre 16
- C. Cohen-Tannoudji, B. Diu et F. Laloë, Mécanique quantique [détail des éditions], chapitre 11
- (en) Cet article est partiellement ou en totalité issu d'une traduction de l'article de Wikipédia en anglais intitulé «Perturbation theory (quantum mechanics) ».
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

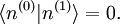
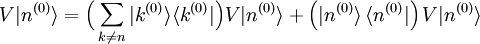
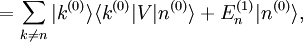
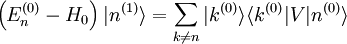
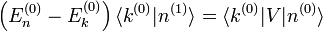
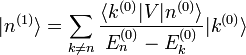
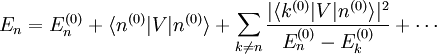
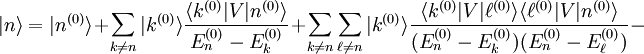
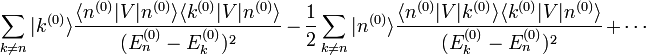
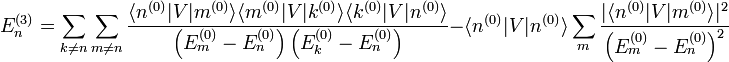
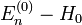
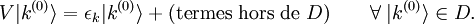
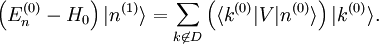
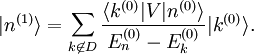
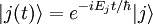
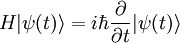
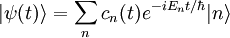
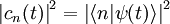
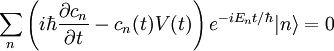
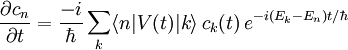
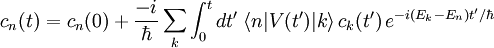
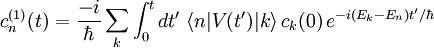

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité