Observable

Dans le formalisme de la mécanique quantique, une opération de mesure est représentée par ce qu'il est convenu d'appeler une observable.

Catégories :

Mécanique quantique - Physique quantique

Source image : www.rh-experts.fr
Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur.

Page(s) en rapport avec ce sujet :

Une sortie à utiliser pour rendre le dispositif observable est la position.... La dynamique de l'observateur est donnée par les valeurs propres de la matriceA... (source : montefiore.ulg.ac)
On remarque alors fréquemment que le diamètre observable est nettement plus petit.... avec leur métrique propre, c'est-à-dire la métrique où la distance entre... (source : yann-ollivier)
généralise à tout l'espace des états E dans le cas d'une observable... une observable est diagonale dans la base constituée par ses vecteurs propres.... Ces états propres doivent continuer à pouvoir apporter une base de l'espace des ... (source : magestik.free)

Dans le formalisme de la mécanique quantique, une opération de mesure (c'est-à-dire obtenir la valeur ou un intervalle de valeurs d'un paramètre physique, ou d'une façon plus générale une information sur un dispositif physique) est représentée par ce qu'il est convenu d'appeler une observable.

Définition formelle

Une observable est formalisée mathématiquement par un opérateur agissant sur les vecteurs d'un espace de Hilbert 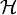$\mathcal{H}$ (chaque état quantique étant représenté par un vecteur dans cet espace).

Le sens de cet opérateur observable est de donner la possibilité de décomposer un état quantique quelconque 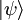$|\psi\rangle$ (donc un vecteur quelconque de l'espace de Hilbert) en une combinaison linéaire d'états propres, chacun de ces états étant un état envisageable résultant de l'opération de mesure.

Soient 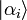$|\alpha_i\rangle$ les vecteurs propres de 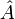$\hat{A}$ (peut-être en nombre illimité selon l'observable).

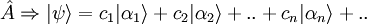
$\hat{A} \Rightarrow |\psi\rangle = c_1 |\alpha_1\rangle + c_2 |\alpha_2\rangle + .. + c_n |\alpha_n\rangle + ..$

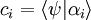$c_i = \langle\psi|\alpha_i\rangle$ étant le cœfficient complexe de cette combinaison linéaire.

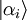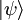Ce cœfficient donne la probabilité pour qu'un état propre $\left| \alpha_i \right\rangle$ soit le résultat de la mesure d'un état quantique $|\psi\rangle$ :

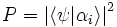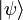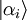$P = {|\langle\psi |\alpha_i\rangle|}ˆ2$ (en supposant que $\left| \psi \right\rangle$ et $\left| \alpha_i\right\rangle$ soient normés)

La totalité des vecteurs propres 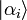$|\alpha_i\rangle$ n'est autre que la totalité des résultats envisageables de l'opération de mesure formalisée par l'observable.

Les états qui s'expriment avant la mesure sous la forme simple 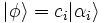$|\phi\rangle = c_i |\alpha_i\rangle$ sont nommés état propre ou état pur. En règle générale, un état quantique n'est pas pur et sont des états juxtaposés, pour cette observable.

Un état peut être pur selon une observable donnée, et être juxtaposé selon une autre observable. C'est d'ailleurs la raison principale du principe d'incertitude d'Heisenberg : un état quantique qui est pur pour une observable (et qui possède par conséquent une valeur précise pour cette observable), peut avoir tout un ensemble de valeurs envisageables pour une autre observable.

Après l'opération de mesure, le dispositif physique mesuré sera dans l'un des états propres définis par l'observable (postulat d'effondrement de la fonction d'onde)

Propriétés de l'opérateur Observable

Cet opérateur doit posséder les propriétés suivantes pour pouvoir être qualifié d'observable :

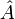$\hat{A}$ doit être un opérateur linéaire.
Les valeurs propres de 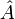$\hat{A}$ , c'est à dire les résultats envisageables de l'opération de mesure, doivent être des nombres réels. Ceci est assuré si 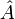$\hat{A}$ est un opérateur hermitien.
Les vecteurs propres de 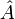$\hat{A}$ doivent être orthogonaux. Ceci est essentiel pour une observable car une fois qu'un état quantique possède une valeur définie, celle-ci doit rester la même si on applique de nouveau le même opérateur de mesure. La probabilité de trouver, comme résultat d'une seconde application de l'opérateur, un autre vecteur propre doit par conséquent être nulle. Ceci est assuré si et uniquement si les vecteurs propres sont orthogonaux.
Les vecteurs propres de 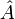$\hat{A}$ doivent former une base de 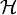$\mathcal{H}$ . Cela assure que tout état quantique (tout vecteur de 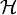$\mathcal{H}$ ) est mesurable par cet opérateur. C'est cette base qui caractérise l'observable. Passer d'une observable à une autre (par exemple de la position à l'impulsion) équivaut à examiner le vecteur représentant l'état quantique dans une base ou dans une autre.
Les vecteurs propres de 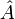$\hat{A}$ doivent être normalisables. En effet, si un vecteur propre n'est pas normalisable, la probabilité d'obtenir cet état propre comme résultat d'une mesure sera nulle. Cette dernière propriété n'est pas strictement indispensable pour que 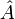$\hat{A}$ soit une observable théorique, mais elle l'est pour que 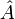$\hat{A}$ soit une observable correspondant à une opération de mesure réelle. A titre d'exemple, la position ou l'impulsion ne sont pas des observables normalisables (ce qui est logique, car étant des variables continues, la probabilité d'obtenir une position ou une quantité de mouvement précise est effectivement nulle).

Exemples d'observables

l'hamiltonien 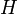$H\,$ (associé à l'énergie du dispositif)
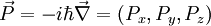
l'impulsion $\vec{P} = -i\hbar\vec\nabla =(P_x,P_y,P_z)\,$
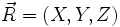la position $\vec{R}=(X,Y,Z)\,$ .
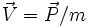
la vitesse $\vec{V}=\vec{P}/m \,$
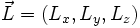
le moment cinétique orbital $\vec{L}=(L_x,L_y,L_z)\,$
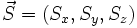
le spin $\vec{S}=(S_x,S_y,S_z)\,$
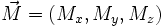
le moment magnétique $\vec{M}=(M_x,M_y,M_z)\,$

Observables non normalisables : utilisation de projecteurs

Dans le cas où les vecteurs propres de l'opérateur ne sont pas normalisables, il est indispensable, pour pouvoir calculer des probabilités utilisables, d'employer un autre type d'observable : des projecteurs.

L'observable 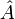$\hat{A}$ , non normalisable, ayant un nombre illimité de valeurs propres, peut être remplacé par un ensemble fini de projecteurs $E i$ tels que :

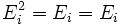$E_iˆ2 = E_i = E_i$ ⁺ (définition d'un projecteur)
$E 1 + E 2 +.. + E n = I$ , $I$ étant l'opérateur identité sur $\mathcal{H}$ .
$E i E j = 0$ si i ≠ j (projecteurs orthogonaux)

Cet ensemble de projecteur est nommé ensemble complet de projecteurs orthogonaux. On a alors : 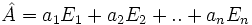$\hat{A} = a_1 E_1 + a_2 E_2 + .. + a_n E_n$

L'opérateur est alors dégénéré, dans le sens où les espaces propres (sous-espace vectoriel correspondants à une valeur propre donnée) des projecteurs possèdent plus d'une dimension.

Le cas typique et particulièrement utilisé d'opérateur dégénéré utilisant les projecteurs est la question OUI/NON où n=2, et où les valeurs propres de l'opérateur sont fixées à 1 pour "OUI" et 0 pour "NON". Cette observable est alors défini par un seul projecteur E, et tout état quantique 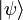$\left| \psi \right\rangle$ peut s'écrire comme :

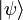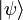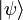
$\left| \psi \right\rangle$ = E $\left| \psi \right\rangle$ + (I-E) $\left| \psi \right\rangle$

A titre d'exemple, pour l'observable "position", on peut calculer un opérateur dont la valeur propre est 1 si la position est dans un certaine zone, et 0 sinon.

Le cinquième postulat ne s'applique pas à un opérateur dégénéré. Il est remplacé dans ce cas par le postulat de projection, voisin, qui stipule que :

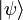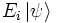Si le résultat d'une mesure d'un état quantique $\left| \psi \right\rangle$ est une certaine valeur propre $a i$ (correspondant au projecteur $E i$ ), alors l'état propre du dispositif est $E_i\left| \psi \right\rangle$ .
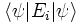
La probabilité d'obtenir la valeur propre $a i$ est $\langle \psi | E_i | \psi \rangle$

Recherche sur Amazone (livres) :

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Observable.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.