Contrafactualité
Selon la mécanique quantique, des évènements contrefactuels, qui auraient pu se produire mais qui ne se sont pas produits, influent sur les résultats de l'expérience.
Recherche sur Google Images :
Source image : fr.wikipedia.org Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- contrafactualité. ?Si en C d. Si en C détecteur photon tecteur photon... contrafactualité. ?OR si photon d. OR si photon détect tecté en Y, c... (source : therapeutia)
Selon la mécanique quantique, des évènements contrefactuels, qui auraient pu se produire mais qui ne se sont pas produits, influent sur les résultats de l'expérience.
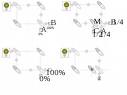
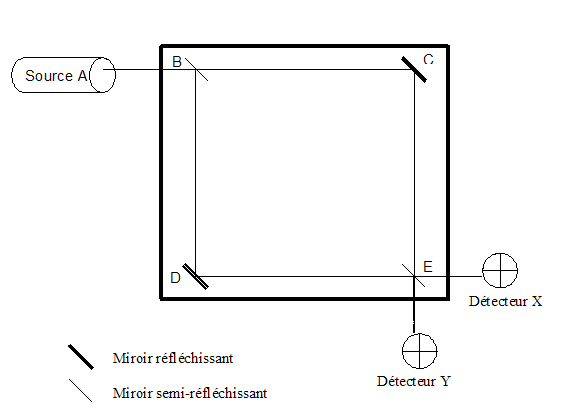
Considérons le système suivant :
Un photon unique est émis par la Source A. On peut démontrer (et vérifier expérimentalement) que seul le détecteur X enregistre la sortie du photon de ce système. Si on ne considère pas les lois quantiques, les détecteurs X et Y auraient une chance identique de détecter le photon à la sortie du système. Ce phénomène est dû à l'état juxtaposé que prend le photon à la sortie du miroir semi réfléchissant B : |\Photon transmis> + |Photon réfléchi>. Une interférence, du même type que celle de l'expérience des fentes d'Young, a alors lieu en E et rend nulle la probabilité que le photon soit détecté en Y.
Une réflexion sur un miroir introduit un déphasage de 1/4 de longueur d'onde. Soit la notation 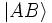 pour noter la fonction d'onde du quanta entre A et B,
pour noter la fonction d'onde du quanta entre A et B, 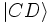 entre C et D etc.
entre C et D etc.
On a alors 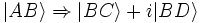 . Le nombre i (i² = -1) représente le décalage de 1/4 de longueur d'onde,
. Le nombre i (i² = -1) représente le décalage de 1/4 de longueur d'onde, 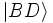 étant l'état réfléchi.
étant l'état réfléchi.
Or
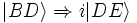 (réflexion sur D) et
(réflexion sur D) et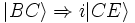 (réflexion sur C)
(réflexion sur C)
donc
Cette fonction d'onde représente l'état juxtaposé du quanta juste avant d'arriver sur E.
D'autre part, on a :
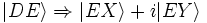 et
et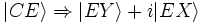
donc l'état juxtaposé juste avant E 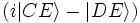 se transforme en :
se transforme en :
Au final : 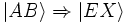 (le facteur -2 étant physiquement sans signification). Le quanta ne peut être détecté que par le détecteur X.
(le facteur -2 étant physiquement sans signification). Le quanta ne peut être détecté que par le détecteur X.
Cette expérience est particulièrement identique dans l'esprit à celle des fentes d'Young, mais sert à plus de mettre en évidence la contrafactualité des phénomènes quantiques :
Modifions ce système pour que C soit désormais un détecteur de photon, du même type que X ou Y. On constate alors (théoriquement et expérimentalement) les faits suivants :
- Soit le photon est détecté par C (probabilité ½)
- Soit les détecteurs X et Y ont une chance identique de détecter le photon (probabilité ¼ et ¼)
C'est ici qu'intervient la contrafactualité : si un photon est détecté en Y, c'est par conséquent que le détecteur C aurait pu détecter le photon (mais il ne l'a pas détecté, sinon le photon n'aurait pu être détecté par Y, ayant déjà été détecté en C). Un évènement contrafactuel modifie par conséquent bel et bien les résultats de l'expérience.
Une variante de ce système est le problème d'Elitzur-Vaidman. Admettons qu'on produit des bombes atomiques qui soient déclenchées par un détecteur ultrasensible : la bombe explose si un seul photon est détecté par le détonateur. Ce détecteur possède aussi les propriétés suivantes :
- Il est peu fiable (mais soit il fonctionne toujours, soit il ne fonctionne jamais)
- S'il ne fonctionne pas, il se comporte comme le miroir réfléchissant C
- Il n'y a pas d'autre moyen de tester ce détecteur qu'en l'utilisant associé à la bombe.
Le gouvernement veut disposer d'un stock de bombes fiables, dont le fonctionnement du détecteur est garanti. Comment tester le détecteur sans faire exploser l'ensemble des bombes fiables ?
La physique quantique nous en donne le moyen : plaçons une bombe en C, et envoyons un photon en A. Si le photon est détecté en Y c'est que le détecteur de la bombe aurait pu détecter le photon, et par conséquent la bombe est certifiée 100% fiable. Mais elle n'a pas explosé.
Si le photon est détecté par X, on ne peut conclure sur la fiabilité de la bombe. Évidemment, si la bombe explose c'est qu'elle était fiable. En itérant le processus, en remettant en jeu les bombes n'ayant pas explosé et associées à une détection en X, on peut certifier jusqu'à 1/4 + 1/4.1/4 + 1/4.1/4.1/4 + … = 1/3 des bombes initiales.
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 12/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

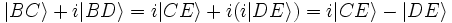
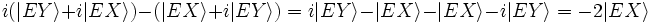

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité