Moment cinétique orbital
Le moment cinétique orbital est un concept de la mécanique quantique. C'est un cas spécifique de moment cinétique quantique.
Recherche sur Google Images :

Source image : diffusion.ens.fr Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- Au moment cinétique orbital est associé un moment magnétique.... défini par une valeur de l, s, j, i et f l'opérateur H peut s'écrire sous la forme :... (source : ozone.obspm)
Introduction
Le moment cinétique orbital est un concept de la mécanique quantique. C'est un cas spécifique de moment cinétique quantique.
Ressemblances avec la mécanique classique
Le moment cinétique orbital correspond à la rotation d'une particule autour d'un noyau, comme la rotation d'un électron autour d'un noyau dans un atome.
On différencie le moment cinétique orbital du moment cinétique intrinsèque, interprétable par la rotation d'une particule élémentaire sur elle-même (on parle de spin de l'électron, par exemple).
Tout moment cinétique est quantifié en mécanique quantique (voir l'article moment cinétique quantique), c'est-à-dire que le moment cinétique ne peut prendre que des valeurs discrètes bien précises. C'est une des propriétés principales de la théorie quantique.
Formules et formalisme quantique
L'opérateur de moment cinétique orbital est noté 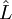 et on le définit par la relation suivante (analogue à celle de la mécanique classique) :
et on le définit par la relation suivante (analogue à celle de la mécanique classique) :
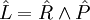 représentant un produit vectoriel.
représentant un produit vectoriel.
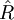 est l'opérateur position et
est l'opérateur position et 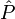 l'opérateur impulsion, qui a pour composantes cartésiennes en représentation position :
l'opérateur impulsion, qui a pour composantes cartésiennes en représentation position :
En représentation position, les composantes cartésiennes de l'opérateur 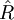 sont simplement :
sont simplement :
D'après ces définition, les composantes cartésiennes de l'opérateur de moment cinétique orbital s'écrivent :
On peut alors calculer les commutateurs de 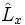 ,
, 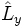 et
et 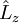 :
:
Moment cinétique total
L'opérateur de moment cinétique total noté 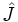 est la somme vectorielle de l'opérateur de moment cinétique orbital noté
est la somme vectorielle de l'opérateur de moment cinétique orbital noté 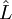 et de l'opérateur de spin (moment cinétique intrinsèque) noté
et de l'opérateur de spin (moment cinétique intrinsèque) noté 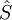 .
.
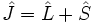
Voir aussi
- Moment cinétique en mécanique classique
- Moment cinétique quantique
- Spin
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

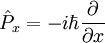
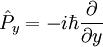
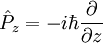
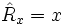
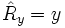
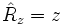
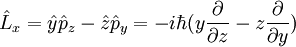
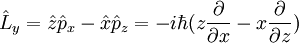
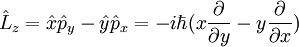
![[\hat L_x, \hat L_y] = i \hbar \hat L_z](illustrations/861c4c3f132e0f442680cf15210fd94a.png)
![[\hat L_y, \hat L_z] = i \hbar \hat L_x](illustrations/023d8de4c789ba138219ab27574e1aa7.png)
![[\hat L_z, \hat L_x] = i \hbar \hat L_y](illustrations/7ab2f6cbdbc904a4ed89d3dab39061e2.png)

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité