Dilaton
En physique théorique, le dilaton désignait à l'origine un champ scalaire théorique qui apparaît dans la théorie de Kaluza-Klein - comme le composé g 55 du tenseur métrique où «5» est la direction circulaire additionnelle -...
En physique théorique, le dilaton désignait à l'origine un champ scalaire théorique (comme le photon réfère à un champ électromagnétique) qui apparaît dans la théorie de Kaluza-Klein - comme le composé g55 du tenseur métrique où «5» est la direction circulaire additionnelle - et obéit à une équation ondulaire non homogène, généralisant l'équation de Klein-Gordon, avec un champ électromagnétique particulièrement fort comme source :
De plus, dans la théorie des cordes, le dilaton est une particule d'un champ scalaire φ qui peut être vu comme la trace du graviton ; un champ scalaire (suivant l'équation Klein-Gordon) qui vient toujours avec la gravité. Quoique la théorie des cordes incorpore naturellement la théorie Kaluza-Klein, les théories des cordes perturbatrices, telles que la théorie des cordes de type I, la théorie des cordes de type II et la théorie des cordes hétérotique, contiennent déjà le dilaton dans le nombre maximal de 10 dimensions. D'autre part, la théorie M en 11 dimensions n'inclut pas le dilaton dans son spectre.
L'exponentielle de sa valeur attendue au vide détermine sa constante de couplage g
Donc la constante de couplage est la variable dynamique dans la théorie des cordes, à la différence du cas de la théorie quantique des champs où elle est constante. Tant que la supersymétrie n'est pas brisée, de tels champs scalaires peuvent avoir des valeurs arbitraires (ce sont des modules). Cependant, la brisure de supersymétrie crée généralement une énergie potentielle pour les champs scalaires et les champs scalaires se localisent proche d'un minimum auquel la position devrait habituellement être calculable dans la théorie des cordes.
Voir aussi
Recherche sur Google Images : |
|
"Lorsqu'une théorie décrit des cordes ..." L'image ci-contre est extraite du site depire.free.fr Il est possible que cette image soit réduite par rapport à l'originale. Elle est peut-être protégée par des droits d'auteur. Voir l'image en taille réelle (520 x 433 - 6 ko - gif)Refaire la recherche sur Google Images |
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 12/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

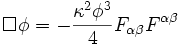
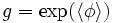

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité