Opérateur d'évolution
En mécanique quantique, l'opérateur d'évolution est l'opérateur qui transforme l'état quantique au temps t 0 en l'état quantique au temps t résultant de l'évolution du dispositif sous l'effet de l'opérateur hamiltonien.
Recherche sur Google Images :
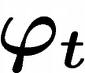
Source image : www.yann-ollivier.org Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- Si l'opérateur d'évolution est unitaire la norme du vecteur d'état se conserve au cours du temps : =... (source : cours.univ-brest)
En mécanique quantique, l'opérateur d'évolution est l'opérateur qui transforme l'état quantique au temps t0 en l'état quantique au temps t résultant de l'évolution du dispositif sous l'effet de l'opérateur hamiltonien.
Position du problème
On considère un hamiltonien composé de deux terme :
où la dépendance temporelle est contenu dans 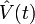 .
.
Lorsque 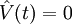 , le dispositif est totalement connu par ses kets
, le dispositif est totalement connu par ses kets 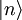 propres et ses valeurs propres En :
propres et ses valeurs propres En :
Définition
Cet opérateur est noté U (t, t0) et on a la relation, qui donne l'état du dispositif au temps t à partir du temps d'origine t0 :
où
Pour le bras, on a alors la relation suivante :
Propriétés
L'opérateur a les propriétés suivantes :
- C'est un opérateur linéaire
- U (t0, t0) = 1
- U (t2, t1) U (t1, t0) = U (t2, t0)
- U (t, t0) est un opérateur unitaire (
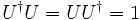 ).
).
Les trois premières propriétés sont des conséquences évidentes de l'équation d'évolution du premier ordre. La dernière propriété vient de ce que la probabilité totale doit etre conservée par l'équation d'évolution.
Comme le dispositif est donné par l'équation de Schrödinger, on a :
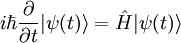 , soit :
, soit :
Dans le cas d'un dispositif quantique dont l'opérateur Hamiltonien 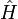 est indépendant du temps, l'opérateur d'évolution s'écrit alors :
est indépendant du temps, l'opérateur d'évolution s'écrit alors :
Pour un dispositif dont le Hamiltonien est dépendant du temps, on peut résoudre par itération l'équation différentielle satisfaite par l'opérateur U. On obtient :
L'écriture de cette expression peut etre simplifiée en introduisant l'opérateur de produit chronologique tel que :
où dans le membre de gauche l'ordre des temps est quelconque, et dans le membre de droite le permutation σ de la totalité  est telle que :
est telle que :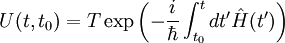
Cette relation est utilisée en théorie quantique des champs pour la construction des diagrammes de Feynman.
Lien avec les autres représentations
L'opérateur d'évolution permet d'établir l'équivalence entre la représentation de Schrœdinger et la représentation de Heisenberg. Dans la représentation de Schrödinger, les opérateurs sont indépendants du temps et les états sont dépendants du temps. Dans la représentation de Heisenberg, les opérateurs sont dépendants du temps et les états indépendants du temps. Le passage d'une représentation à l'autre se fait au moyen de l'opérateur d'évolution :
| Représentation : | |||
| Heisenberg | Interaction | Schrödinger | |
| Ket | constant | 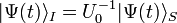 |
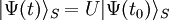 |
| Observable | AH (t) = U − 1ASU | 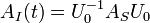 |
constant |
| Opérateur d'évolution | 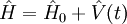 |
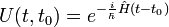 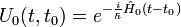 |
|
| Mécanique quantique : Théorème d'Ehrenfest • Équation de Schrödinger • Propagateur | |||
Bibliographie
- Albert Messiah, Mécanique quantique [détail des éditions]
- J. L. Basdevant, J. Dalibard, Mécanique quantique [détail des éditions]
- C. Cohen-Tannoudji, B. Diu et F. Laloë, Mécanique quantique [détail des éditions]
- Lev Landau et Evguéni Lifchitz, Physique théorique, tome 3 : Mécanique quantique, éd. MIR, Moscou [détail des éditions]
- Lev Landau et Evguéni Lifchitz, Physique théorique, tome 4 : Électrodynamique quantique, éd. MIR, Moscou [détail des éditions]
- N. M. Bogoliubov et D. V. Shirkov, Introduction à la théorie des champs quantifiés (Dunod)
- D. Kastler, Électrodynamique Quantique (Dunod)
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

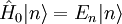
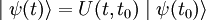
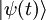 représente le
représente le 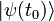 représente le
représente le 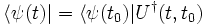
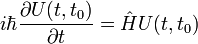
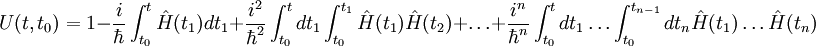
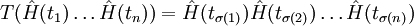
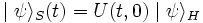
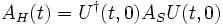

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité