Unitarité

La fonction d'onde 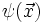d'un dispositif quantique, comme l'électron par exemple, sert à déterminer la probabilité de présence de ce dernier dans une petite boîte de volume 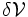centrée en 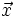par

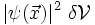
Et comme la probabilité totale de trouver le dispositif quelque part doit être d'un, il en découle qu'on doit avoir

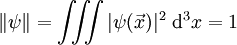
en intégrant sur tout l'espace.

Les fonctions d'onde dont l'intégrale sur tout l'espace est identique à 1 sont appelées fonction d'onde normalisable, et l'état quantique correspondant un état quantique normalisable. Mais l'ensemble des fonctions d'ondes ne sont pas normalisables, comme celle correspondant à l'état de quantité de mouvement.

L'unitarité est une propriété de l'ensemble des fonctions d'ondes normalisables.

Unitarité

Cette propriété de la fonction d'onde doit être vraie à tout instant donné. L'unitarité peut par conséquent s'exprimer sous la forme :

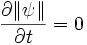
L'équation de Schrödinger qui fixe l'évolution de la fonction d'onde doit satisfaire cette contrainte. On rappelle que cette équation s'écrit

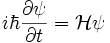
Où 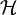est le hamiltonien du dispositif. Il en résulte tandis que le hamiltonien doit être un opérateur hermitien^[1], c'est-à-dire que les valeurs propres (et par conséquent les quantités mesurées) de l'opérateur sont des nombres réels, ce qui correspond bien à la réalité.

Le critère d'unitarité peut s'exprimer d'une façon plus générale comme la conservation du produit scalaire dans le temps. Soient deux états quantiques θ et ψ, on doit alors avoir :

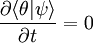
la conservation de la norme n'étant que le cas spécifique où θ = ψ.

On peut démontrer aussi que l'équation de Schrödinger conserve effectivement le produit scalaire (pourvu, toujours, que le hamiltonien soit hermitien).

Opérateur

L'équation de Schrödinger étant unitaire, elle peut être représentée par un opérateur unitaire dans le formalisme de la mécanique quantique.

Démonstration : représentons l'équation de Schrödinger par un opérateur linéaire U : ψ (t) = U (t) ψ (0) .

Nous savons que l'équation de Schrödinger préserve le produit scalaire, donc : .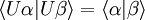

D'autre part, une propriété des matrices adjointes comparé au produit scalaire assure que .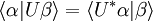

Donc :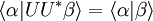

D'où UU ^* = U ^* U = I ce qui est caractéristique d'un opérateur unitaire.

Unitarité et mesure

Article détaillé : Problème de la mesure quantique.

Le cinquième postulat de la mécanique quantique affirme la réduction de la fonction d'onde à un des états propres du hamiltonien immédiatement après une observation.

Ce postulat est une violation directe (et l'unique) du principe d'unitarité de la mécanique quantique. En effet la réduction de la fonction d'onde correspond à une projection, qui ne conserve pas le produit scalaire.

Il met en exergue le fait que l'observation d'un dispositif microscopique par un appareil macroscopique est une interaction violente pour le dispositif quantique. Les travaux sur la décohérence quantique cherchent à montrer, jusqu'ici avec succès, que si on étudie plus exactement le mécanisme d'observation alors il est envisageable de montrer que le cinquième postulat n'est pas rigoureusement exact mais plutôt une approximation. Dans cette approche, l'apparente réduction de la fonction d'onde n'est qu'une localisation progressive autour d'un des états propres du hamiltonien et est une conséquence de l'équation de Schrödinger pour le dispositif physique total constitué du dispositif observé mais aussi de l'observateur.

Notes

Voir aussi