Représentation d'interaction
La représentation d'interaction ou représentation de Dirac de la mécanique quantique est une manière de traiter les problèmes dépendant du temps.
Recherche sur Google Images :
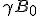
Source image : forums.futura-sciences.com Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- Cas général∼ : opérateurs rotation 3. Exemples IV. Matrices rotation... Développement en perturbation (représentation d'interaction)... Largeur et temps de vie d'un dispositif instable, états atomiques excités (ordres de grandeur)... (source : books.google)
- Représentation de l'algèbre des opérateurs de moment angulaire... 467 13.3 Renversement du temps 468 13.4 Opérateurs anti-unitaires 470 13.5 Dispositifs... (source : springer)
La représentation d'interaction ou représentation de Dirac de la mécanique quantique est une manière de traiter les problèmes dépendant du temps.
Condition d'application de la représentation d'interaction
Dans la représentation d'interaction, on applique les hypothèses suivantes :
On considère un hamiltonien ayant la forme suivant :
où 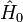 est constant dans le temps et
est constant dans le temps et 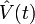 décrit une interaction perturbative qui peut dépendre du temps.
décrit une interaction perturbative qui peut dépendre du temps.
- Les états propres sont dépendants du temps
- Les opérateurs sont aussi dépendants du temps
- La dynamique des états est décrite suivant la représentation de Schrödinger alors que la dynamique des opérateurs est décrite suivant la représentation de Heisenberg.
- La représentation de Dirac ne s'applique efficacement qu'à certains problèmes. L'exemple le plus parlant est celui des perturbations dépendant du temps.
Propagateurs
Pour reconnaitre qu'on travaille dans la représentation d'interaction, les états et les opérateurs seront suivis de l'indice "I" (comme interaction). Le sens de cette représentation tient en ce que la dépendance en temps due à 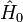 sera prise en compte dans la dépendance explicite des observables selon le temps et la dépendance en temps due à
sera prise en compte dans la dépendance explicite des observables selon le temps et la dépendance en temps due à 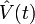 dans le développement de la fonction d'onde. C'est une autre façon de décrire la même physique. Ceci veut dire que les grandeurs physiques significatives sont inchangées.
dans le développement de la fonction d'onde. C'est une autre façon de décrire la même physique. Ceci veut dire que les grandeurs physiques significatives sont inchangées.
Il y a deux opérateurs d'évolution dans le temps :
- l'opérateur "normal" relatif à l'hamiltonien complet
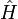
- l'operateur relatif à l'hamiltonien non perturbé
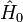
Définition des hamiltoniens et fonction d'onde d'interaction
L'opérateur dépendant du temps 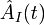 s'écrit comme dans la représentation de Heisenberg
s'écrit comme dans la représentation de Heisenberg
l'état dépendant du temps 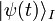 n'est accessible qu'indirectement, par réduction (dans la représentation de Schrödinger) de l'état de la dynamique complète
n'est accessible qu'indirectement, par réduction (dans la représentation de Schrödinger) de l'état de la dynamique complète 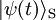 , pour définir.
, pour définir.
À partir de là nous définissons aussi l'opérateur dépendant du temps HI (t) :
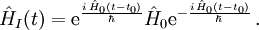
Équations d'évolution de la fonction d'onde et des observables
L'évolution de la fonction d'état s'écrit dans cette représentation :
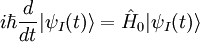 .
.
Cette équation est connue sous le nom d'équation de Schwinger-Tomonaga. L'évolution de la grandeur physique représentée par l'opérateur A s'écrit :
| Représentation : | |||
| Heisenberg | Interaction | Schrödinger | |
| Ket | constant | 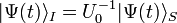 |
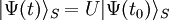 |
| Observable | AH (t) = U − 1ASU | 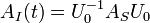 |
constant |
| Opérateur d'évolution | 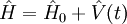 |
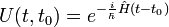 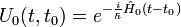 |
|
| Mécanique quantique : Théorème d'Ehrenfest • Équation de Schrödinger • Propagateur | |||
Voir aussi
- A. Messiah, Mécanique Quantique (Dunod)
- J. L. Basdevant, Cours de mécanique quantique de l'école Polytechnique (Ellipses)
- J. J. Sakurai et s. F. Tuan, Modern Quantum Mechanics, Benjamin-Cummings 1985, Reading, Addison-Wesley 2003
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

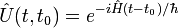
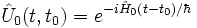
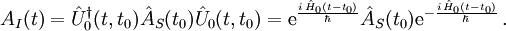
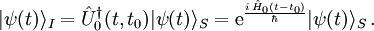
![i\,\hbar\frac{{\rm d} \hat A_I}{{\rm d}t}=\left[\hat A_{\rm I}(t),\hat H_0\right] +\frac{\partial \hat A_I }{\partial t}](illustrations/cea4493ff09e4429441cac3481758178.png)

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité