Puits de potentiel semi-classique

Soit une particule de masse m, sur un axe x'Ox, soumise à une force d'énergie potentielle V, en "cuvette". L'équation classique du mouvement entre les deux points "tournants" x1 et x2 tels que V = E a été étudiée dans l'article puits de potentiel.

Catégories :

Article à recycler (physique) - Mécanique quantique - Physique quantique

Source image : dictionnaire.sensagent.com
Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur.

Page(s) en rapport avec ce sujet :

Puits de potentiel généralisés et asymptotique semi - classique Helffer B.... Nous obtenons aussi des résultats près du minimum de l'énergie classique.... (source : cat.inist)
Semi -classical and high energy asymptotics of the scattering phase for.... Approximation semi - classique de la phase de diffusion pour un potentiel.... B. ; Robert, D. Puits de potentiel généralisés et asymptotique semi - classique.... (source : math.sciences.univ-nantes)

Soit une particule de masse m, sur un axe x'Ox, soumise à une force d'énergie potentielle V (x), en "cuvette". L'équation classique du mouvement entre les deux points "tournants" x1 (E) et x2 (E) tels que V (x) = E a été étudiée dans l'article puits de potentiel.

Le mouvement est périodique de période T (E), l'orbite dans l'espace des phases (x, p) est fermée, et parcourue dans le sens négatif avec cette période. Elle enclôt une aire homogène à une action A (E), dont la dérivée est T (E).

En mécanique dite semi-classique, on considère que les actions sont des multiples entiers de la constante de Planck h, soit A (E) = n h, mais on est bien conscient que le niveau le plus bas d'énergie doit correspondre à celui de l'oscillateur harmonique "osculateur", par conséquent on rédigé plutôt :

A(E) = (n-1/2) h , n entier positif

[remarque : il est indifférent bien entendu d'écrire n+1/2, avec n entier; le 1/2 est complexe à justifier, sans étude analytique précise dans le plan complexe des points tournants. Cf le livre de Sommerfeld].

Cette formule définit en gros le spectre d'énergie des états liés de la cuvette, E (n).

On examinera les cuvettes étudiées auparavant.

Cela permettra ensuite, par "prolongement analytique", d'étudier aisément les barrières de potentiel et l'effet tunnel.

Oscillateur harmonique

la cuvette est du type V (x) = 1/2 k x²

On trouve facilement que les niveaux sont :

 , n entier (positif ou nul),

puisque A (E) = T°. E ; le niveau essentiel $E_0 = [0 + \frac{1}{2}] \hbar \omega_0$ pouvant se calculer joliment par une astuce sur les inégalités d'Heisenberg (cf saturation des inégalités d'Heisenberg).

Chute libre et rebond

Ce cas a été étudié dans diagramme horaire, sous le nom de cuvette de Torricelli. Le point matériel, de masse m, tombe sous l'effet de la pesanteur g, d'une hauteur H et rebondit élastiquement au sol avec la vitesse V° = sqrt (2gH) (formule dite de Torricelli).

L'orbite périodique, d'énergie E, dans l'espace des phases s'en déduit immédiatement : c'est la portion z>0 de la parabole : mv = +/- m. sqrt[ 2g. (H-z) ], dont l'aire A (E) est donnée par l'antique formule d'Archimède : A (E) = 2/3. mV°. H. 2, soit A (E) ∼Eˆ (3/2). Immédiatement, on en tire le spectre d'énergie :

 $E n = n 2 / 3 E 1$

avec 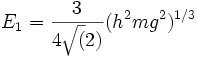$E_1 = \frac{3}{4\sqrt(2)} (hˆ2mgˆ2)ˆ{1/3}$ ,

dont on vérifie facilement l'homogénéité.

Pour le calcul du niveau essentiel, on effectuera le raisonnement simpliste habituel : E = Ec + Ep minimale soit :

-hˆ2/mHˆ3 + mg = 0, soit Eo ∼ E1 (inutile en semi-classique d'essayer de pousser plus avant : le calcul correct sera fait en Quantique)

Puits illimité

L'orbite de phase du puits illimité est vraiment la plus simple de toute : c'est un rectangle de largeur a et de quantité de mouvement +/- sqrt (2mE), d'où l'aire A (E) = 2sqrt (2). sqrt (mEa²). On en déduit immédiatement le spectre :

$E n = n 2 E 1$ ,

avec 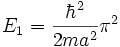$E_1 = \frac{\hbarˆ2}{2maˆ2}\piˆ2$ ,

ce qui est par hasard la formule EXACTE de la Quantique.

Puits fini

Cette fois, pour un puits de profondeur E°, la mécanique semi-classique est impuissante à résoudre le phénomène suivant : les niveaux d'énergie se rapprochent lorsque on monte en énergie. Le problème se résout idéalement en Quantique.

Ici, pour faire simple, nous indiquerons la suggestion de Gamow : la particule est évanescente sur une distance d (E) =∼ sqrt (h²/2m (E°-E) et il faut par conséquent prendre comme largeur du puits non pas a, mais a +2d (E). Ceci redonne qualitativement l'allure du spectre; quantitativement si on se laisse semi-empiriquement la latitude du cœfficient numérique devant d (E), de façon à avoir le même nombre (fini) de niveaux d'énergie dans le puits, l'accord n'est pas si mauvais. Inutile toujours une fois de poursuivre plus avant.

Puits type Ep = 1/k A. |x|ˆk

On vient de traiter k = 2, k = 1 et k = 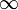$\infty$ .

On généralise facilement le théorème d'Archimède sur la quadrature de la parabole : l'action A (E) vaut :

A (E) = 2 mV°. H. k/ (k+1) ∼ sqrt (E). Eˆ (1/k), d'où le spectre :

,avec  $E 1 = C k (A 2 h 2 k / m k) 1 / (2 + k)$ ,

dont on peut vérifier l'homogénéité. On retrouve bien les cas k = 2, 1, illimité.

Des considérations à partir du théorème du viriel sont envisageables aussi pour ces cas.

Dans le cas où les puits sont finis, on pourra appliquer la règle de Gamow, ce qui redonne en gros, le nombre fini de niveaux d'énergie N (E°).

Remarque importante :

on peut être tenté de généraliser au cas de k négatifs : la formule précédente montre qu'il faut être prudent avec k = - 2 (force en 1/xˆ3) ;

Atome d'hydrogène : mais il se trouve qu'elle donne le bon résultat pour k= -1 :

avec E1 = 13.6eV, cela peut être retenu comme moyen mnémotechnique, pour les états ns de l'atome d'hydrogène (ici encore, on peut consulter l'article saturation des inégalités d'Heisenberg). Par contre, on n'a aucun moyen ici pour retrouver la dégénérescence 2nˆ2 de l'atome-3D.

Ainsi, l'étude semi-classique sert à trouver d'importantes relation entre spectre En et potentiel Ep (x). Réciproquement, peut-on à partir du spectre discret remonter à Ep (x). C'est le particulièrement célèbre problème de Mac Kac : peut-on entendre la forme d'un tambour? Ce problème a été traité dans le cas classique (cf puits de potentiel). Mais il est bien plus ardu en Quantique, et en semi-classique.

Voir aussi

Recherche sur Amazone (livres) :

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Puits_de_potentiel_semi-classique.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.