Loi de Beer-Lambert
La loi de Beer - Lambert, aussi connue comme la loi de Beer-Lambert-Bouguer et chez les francophones quelquefois même simplement comme la loi de Bouguer, est une relation empirique reliant l'absorption de la lumière aux propriétés des milieux dans lesquels elle passe.

Catégories :
Optique ondulatoire - Spectroscopie - Physique quantique - Loi en physique - Méthode de la biochimie
Recherche sur Google Images :

Source image : www.intellego.fr Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- La loi de Beer-Lambert est une relation donnant la variation de ... cuve de longueur l (généralement 1 cm) contenant une solution de concentration C mol.... (source : sciences-en-ligne)
- La loi de beer lambert est utilisée dans de nombreux dosages d'espèces chimiques colorées.... Soit une radiation monochromatique de longueur d'onde fixe traversant un échantillon... c : la concentration de la solution en mol/L... (source : lachimie)
- avec l la largeur de la cuve, C la concentration de la solution et el un.... Ø La loi de Beer-lambert est -elle vérifiée pour le diiode à la longueur d'onde... (source : gistlabs.homelinux)
La loi de Beer-Lambert, aussi connue comme la loi de Beer-Lambert-Bouguer et chez les francophones quelquefois même simplement comme la loi de Bouguer, est une relation empirique reliant l'absorption de la lumière aux propriétés des milieux dans lesquels elle passe.
La loi de Beer-Lambert établit une proportionnalité entre la concentration d'une entité chimique en solution, l'absorbance de celle-ci et la longueur du trajet parcouru par la lumière dans la solution.
Enoncé
Soit un rayonnement électromagnétique de longueur d'onde λ (p. ex. lumière), traversant un milieu transparent. L'intensité de ce rayonnement subit une diminution exponentielle selon la distance parcourue et de la densité des espèces absorbantes dans ce milieu.
- I0 est l'intensité de la lumière incidente.
- I est l'intensité de la lumière sortante.
- α est le cœfficient d'absorption (en m2·mol-1 ou en m3·mol-1·cm-1).
- X est la longueur du trajet optique (en m ou en cm).
- r est la concentration de l'entité absorbante, atomes ou molécules, dans le milieu (en mol·m-3).
La valeur du cœfficient d'absorption α fluctue entre différents matériaux et aussi avec la longueur d'onde pour un matériau spécifique. Elle est définie par l'équation :
- ω est la pulsation angulaire du rayonnement électromagnétique.
- k est le cœfficient d'extinction linéique, il exprime l'atténuation de l'énergie du rayonnement électromagnétique à travers le milieu.
- c est la célérité du rayonnement électromagnétique dans le vide.
Dérivation
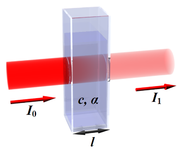
L'absorption d'un faisceau lumineux monochromatique dans un milieu homogène et isotrope est proportionnelle à la longueur du trajet optique suivi par cette radiation et la concentration, en solution, ou la pression partielle, en phase gazeuse, des espèces absorbantes[1].
La loi de Beer-Lambert peut s'exprimer ainsi :
Ou encore :
- I / I0 est la transmittance de la solution (sans unité).
- A est l'absorbance ou densité optique à une longueur d'onde λ (sans unité).
- ε est l'absorptivité molaire (aussi nommé cœfficient d'extinction molaire) , exprimée en L·mol−1·cm−1. Elle dépend de la longueur d'onde, la nature chimique de l'entité et la température.
- ℓ est la longueur du trajet optique dans la solution traversée, elle correspond à l'épaisseur de la cuve utilisée (en cm).
- C est la concentration molaire de la solution (en mol. L−1). Dans le cas d'un gaz, C peut être exprimée comme une densité (unités de longueur réciproque au cube, cm−3).
Cette équation est particulièrement utile pour la chimie analytique. En effet, si ℓ et ε sont connus, la concentration d'une substance peut être déduite de la quantité de lumière transmise par elle .
Additivité
À une longueur d'onde donnée λ, l'absorbance A d'un mélange de n espèces absorbantes est la somme des absorbances individuelles :
- Exemple d'application
Soit une solution contenant un mélange de Ni (II) et de Co (II), on cherche à déterminer leurs concentrations respectives CNi et CCo en appliquant la loi de Beer-Lambert.
Pour ceci, on mesure l'absorbance de la solution à deux longueurs d'ondes différentes λa = 393 nm et λb = 510 nm qui correspondent respectivement aux absorbances maximales des deux entités en solution prises chacune à part. On établit alors les équations suivantes :
Connaissant A et ε dans chaque cas, on peut déterminer les concentrations relatives de chaque espèce par simple résolution de ce dispositif d'équations.
N. B. : contrairement aux absorbances, les transmittances de plusieurs entités ne sont pas des grandeurs additives.
Loi de Beer-Lambert dans l'atmosphère
La loi de Beer-Lambert peut être appliquée pour décrire l'atténuation du rayonnement solaire à travers l'atmosphère. Dans ce cas, une partie de cette lumière est diffusée tandis qu'une autre est absorbée par les différents constituants. La loi est exprimée comme suit :
Dans cette équation, τx est le cœfficient de transparence d'un composant x de l'atmosphère, qui peut être :
- a fait références aux aérosols qui absorbent et diffusent la lumière,
- g est un mélange uniforme de gaz (essentiellement, le dioxyde de carbone (CO2) et le dioxygène (O2). Ils sont uniquement absorbants, respectivement, des ultraviolets et des infrarouges),
- NO2 est le dioxyde d'azote (provenant essentiellement de la pollution urbaine, il absorbe uniquement),
- w est l'absorption due à la vapeur d'eau,
- O3 est l'ozone (il absorbe uniquement une partie des ultraviolets),
- r est la diffusion Rayleigh due à l'oxygène (O2) et l'azote (N2) (ce dernier est à l'origine de la couleur bleue du ciel),
- m est le facteur optique de la masse de l'air, identique à 1/cosθ où θ est l'angle que forme les rayons solaires incidents avec le zénith.
Cette équation est utilisée pour déterminer la profondeur optique des aérosols, afin d'étudier leur effets sur le climat, ou pour corriger les abbérations dans les images obtenues par les satellites.
Vérification amusante
Si on fait infuser un sachet de thé dans une casserole et qu'on le retire ensuite, on a la surprise de voir que l'ajout d'une quantité quelconque d'eau pure n'altère en rien la coloration du liquide, aussi contre-intuitif que cela paraisse. La raison en est que le paramètre de concentration diminue précisément dans les mêmes proportions qu'augmente l'épaisseur à traverser.
Une seconde réflexion rend la chose évidente, du fait que la quantité de pigment traversée par la lumière reste obligatoirement la même du fait du parallélisme des parois de la casserole.
Histoire
Cette loi fut découverte par Pierre Bouguer en 1729 et publiée dans son ouvrage “Essai d'Optique sur la Gradation de la Lumière” (Claude Jombert, Paris, 1729), puis reprise par Johann Heinrich Lambert en 1760 et finalement August Beer en 1852 y introduisit la concentration, lui donnant la forme sous laquelle elle est le plus fréquemment utilisée.
Références
Voir aussi
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.
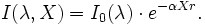
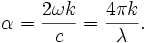
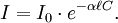
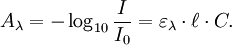
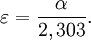
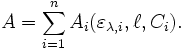
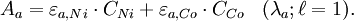
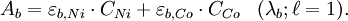
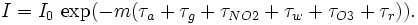

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité