Représentation de Heisenberg
En mécanique quantique, la représentation de Heisenberg est une des trois formulations et modes de traitement des problèmes dépendants du temps dans le cadre de la mécanique quantique classique.
Recherche sur Google Images :
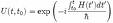
Source image : www.techno-science.net Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- Représentation de Schrödinger 2. Représentation de Heisenberg, ... Largeur et temps de vie d'un dispositif instable, états atomiques excités (ordres de ... (source : offre-de-formations.univ-lyon1)
En mécanique quantique, la représentation de Heisenberg est une des trois formulations et modes de traitement des problèmes dépendants du temps dans le cadre de la mécanique quantique classique. Dans cette réprésentation, les opérateurs du dispositif évolue avec le temps.
Généralités
Le principe de superposition stipule qu'un'état est généralement une combinaison linéaire d'états propres. Dans cette représentation :
- Les états sont indépendant du temps, notés dans la notation de Dirac sous forme de kets
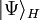
- Les opérateurs sont dépendants du temps.
Cette représentation est à opposer à la représentation de Schrödinger, dans laquelle les operateurs sont indépendants du temps mais opèrent sur des vecteurs d'état qui sont fonction du temps.
La représentation de Heisenberg ne doit pas être confondue avec la «mécanique des matrices», parfois nommée «mécanique quantique de Heisenberg».
Formulation mathématique
Dans le cadre de la représentation de Heisenberg de la mécanique quantique le vecteur d'état 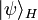 est indépendant du temps, on peut la déterminer ainsi :
est indépendant du temps, on peut la déterminer ainsi :
tandis qu'une observable satisfait à l'équation d'évolution :
La similitude avec la physique classique est évidente en remplaçant le commutateur par un crochet de Poisson.
Opérateur d'évolution
On considère l'opérateur d'évolution temporelle suivant :
avec
Lien avec la représentation de Schrödinger
Soit une observable 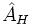 :
:
où 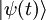 obeit à l'équation de Schrödinger :
obeit à l'équation de Schrödinger :
où 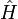 est le hamiltonien, et
est le hamiltonien, et 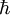 .
.
On en déduit que
donc
puisque 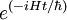 commute avec
commute avec 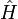 .
.
| Représentation : | |||
| Heisenberg | Interaction | Schrödinger | |
| Ket | constant | 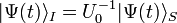 |
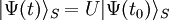 |
| Observable | AH (t) = U − 1ASU | 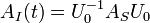 |
constant |
| Opérateur d'évolution | 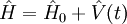 |
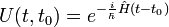 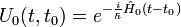 |
|
| Mécanique quantique : Théorème d'Ehrenfest • Équation de Schrödinger • Propagateur | |||
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

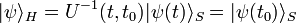
![{d \over {dt}}A_H={1 \over {i\hbar}}[A_H,\hat H]+({{\partial A_H} \over {\partial t}})_{classique}](illustrations/b9d86f689ba09bb5a119df80ade20b88.png)
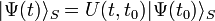
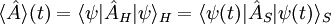
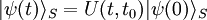
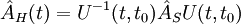
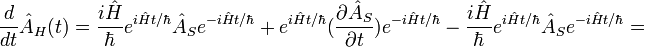
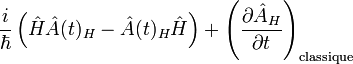

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité