Théorie de jauge

En physique théorique, une théorie de jauge est une théorie des champs basée sur un groupe de symétrie locale, nommé groupe de jauge, définissant une «invariance de jauge».

Catégories :

Théorie de jauge - Théorie quantique des champs - Physique quantique

Source image : www.futura-sciences.com
Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur.

Page(s) en rapport avec ce sujet :

Une théorie de jauge est introduite avec un groupe de jauge SU (H) ∂SU (2) L∂U (1) y'. Dans cette théorie, les quarks se transforment sous la représentation... (source : cat.inist)
Dans la théorie de W-S le groupe de jauge est . 11 apparaît une partie additionnelle dans les .... de la théorie de jauge est que les champs de jauge... (source : hal.archives-ouvertes)
Cette construction de fibré ou théorie de jauge est suggérée en Physique par Hermann Weyl [15], qui lui donne sa forme actuelle (où le groupe de jauge est U... (source : numdam)

En physique théorique, une théorie de jauge est une théorie des champs basée sur un groupe de symétrie locale, nommé groupe de jauge, définissant une «invariance de jauge ». Le prototype le plus simple de théorie de jauge est l'électrodynamique classique de Maxwell.

L'expression «invariance de jauge» a été introduite en 1918 par le mathématicien Hermann Weyl.

Description mathématique

On considère un espace-temps classique modélisé par une variété différentielle lorentzienne à quatre dimensions, pas obligatoirement courbe.

Champs de jauge & espaces fibrés

Les théorie de champs de jauge dans l'espace-temps utilisent la notion d'espace fibré différentiel. Il s'agit toujours d'une variété différentielle, mais de dimension plus grande que celle de l'espace-temps, qui joue ici le rôle d'espace de base du fibré.

On considère plus exactement un fibré principal, dont la fibre s'identifie au groupe de structure qui est un groupe de Lie précisant la symétrie de la théorie, nommée «invariance de jauge».

Un champ de jauge A y apparait comme une connexion, et la forme de Yang-Mills associée F = dA comme la courbure associée à cette connexion.

Principaux groupes de Lie

O (n) est le groupe orthogonal sur 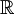$\mathbb{R}$ d'ordre n, i. e. le groupe multiplicatif des matrices n × n réelles orthogonales (vérifiant ^tMM = I_n).
SO (n) est le groupe spécial orthogonal sur 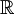$\mathbb{R}$ d'ordre n, i. e. le groupe multiplicatif des matrices n × n réelles orthogonales et de déterminant 1 (vérifiant ^tMM = I_n et det M = 1).
U (n) est le groupe unitaire sur 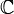$\mathbb{C}$ d'ordre n, i. e. le groupe multiplicatif des matrices n × n complexes unitaires (vérifiant M*M = I_n).
SU (n) est le groupe spécial unitaire sur 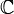$\mathbb{C}$ d'ordre n, i. e. le groupe multiplicatif des matrices n × n complexes unitaires et de déterminant 1 (vérifiant M*M = I_n et det M = 1).

Cas spécifiques

O (1) = {1, -1}
SO (1) = {1}.
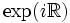
U (1) = SU (1) est le cercle unité complexe. Il est identique à $\exp(i\mathbb{R})$
SO (2) est isomorphe à U (1) : c'est la totalité des rotations du plan laissant 0 invariant.
SO (3) est la totalité des rotations de l'espace à 3 dimensions.

Exemples physiques

Ont été démontrées pertinentes pour le monde réel :

la théorie de jauge classique U (1) , qui s'identifie à la théorie électromagnétique de Maxwell. C'est une théorie abélienne, qui admet des extensions non-abéliennes intéressantes nommées théories de Yang-Mills, basées sur les groupes non-abéliens SU (n) .

Après quantification, deux des théories de Yang-Mills forment l'actuel «modèle standard» de la physique des particules :
- le modèle électro-faible de Glashow, Salam et Weinberg est basé sur le groupe U (1) x SU (2) et décrit de façon unifiée l'électromagnétisme et l'interaction nucléaire faible.
- la chromodynamique quantique est basée sur le groupe SU (3) , et décrit l'interaction nucléaire forte entre les quarks et les gluons.

Voir aussi

Bibliothèque virtuelle

Delamotte, Bertrand ; Un soupçon de théorie des groupes : groupe des rotations & groupe de Poincaré, cours d'introduction pour physiciens (prolégomènes à un cours de théorie quantique des champs) donné en 1995 par Bertrand Delamotte (Laboratoire de Physique Théorique et Hautes Energies, Université Paris 7) au D. E. A. "Champs, Particules, Matières". 127 pages.

Aspects historiques

John D. Jackson & L. B. Okun ; Historical roots of gauge invariance, Review of Modern Physics 73 (2001) 663-680. Texte complet disponible sur l'ArXiv : hep-ph/0012061.

Lochlainn O'Raifeartaigh ; The Dawning of Gauge Theory, Princeton University Press (May 5, 1997), ISBN 0-69-102977-6.

Tian Yu Cao ; Conceptual Developpments of 20th Century Field Theories, Cambridge University Press (1997), ISBN 0-521-63420-2.

Ouvrages d'introduction à la théorie quantique des champs

Michel Le Bellac ; Des phénomènes critiques aux champs de jauge - Une introduction aux méthodes ainsi qu'aux applications de la théorie quantique des champs, InterEditions/Editions du C. N. R. S. (1988), ISBN 2-86883-359-4. Réédité par E. D. P. Sciences.

Ouvrages de mathématiques pour physiciens théoriciens

Theodore Frenkel ; The Geometry of Physics - An introduction, Cambridge University Press (1997), ISBN 0-521-38753-1.

Mikio Nakahara ; Geometry, Topology ans Physics, Institute of Physics Publishing (1990), ISBN 0-85274-095-6.

Charles Nash & Siddharta Sen ; Topology & Geometry for Physicists, Academic Press (1983), ISBN 0-12-514080-0.

Yvonne Choquet-Bruhat & Cécile deWitt-Morette ; Analysis, Manifolds & Physics - Part I : Basics, North-Holland/Elsevier (2^e édition révisée - 1982), ISBN 0-444-86017-7.

Ouvrages de physique pour mathématiciens

Pierre Deligne & Al ; Quantum Fields and Strings : A Course for Mathematicians, Amer Mathematical Society (27 Jan 2000), ISBN 0821820141

Notes et références

Recherche sur Amazone (livres) :

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Th%C3%A9orie_de_jauge.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.