Notation bra-ket
La notation bra-ket a été introduite par Paul Dirac pour favoriser l'écriture des équations de la mécanique quantique, mais également pour souligner l'aspect vectoriel de l'objet représentant un état quantique.
Recherche sur Google Images :

Source image : dictionnaire.sensagent.com Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- Cette nouvelle notation souligne en fait la relation qu'il existe entre bra, ket et le produit scalaire entre kets. Prenons un ket. Son produit scalaire... (source : dictionnaire.sensagent)
- 6 messages - 5 auteurs - Dernier message : 19 oct 2008 Forum de physique - Notation Bra - Ket, LaTeX, Doctorat, Thèse.... fois où j'ai utilisé cette notation c'est pour les produits scalaires.... (source : fr.hypo-theses)
La notation bra-ket a été introduite par Paul Dirac pour favoriser l'écriture des équations de la mécanique quantique, mais également pour souligner l'aspect vectoriel de l'objet représentant un état quantique (voir Axiomes de la mécanique quantique).
Le nom provient d'un jeu de mots avec le terme (en) bracket qui veut dire «crochet de parenthèse», en l'occurrence «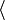 » et «
» et «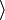 » respectivement nommés «bra» et «ket» (un peu à l'image de babord et de tribord). Cette notation est depuis reprise dans l'étude mathématique de l'algèbre des opérateurs, et dont le champ d'application est plus large.
» respectivement nommés «bra» et «ket» (un peu à l'image de babord et de tribord). Cette notation est depuis reprise dans l'étude mathématique de l'algèbre des opérateurs, et dont le champ d'application est plus large.
L'origine du formalisme
Notation : la notation * veut dire qu'il est question du transposé du conjugué d'un vecteur dont les coordonnées sont des nombres complexes.
On rappelle que les fonctions d'onde quantiques sont des fonctions du temps, des coordonnées spatiales, ou alors d'autres paramètres internes (spins, moments magnétiques, …) :
qu'elles sont solutions de l'équation de Schrödinger :
qu'elles sont normalisées, de sorte que :
et que la valeur d'une grandeur physique A est obtenue par :
La notation de Dirac s'appuie sur l'identification de l'intégrale précédente avec un produit hermitien sur l'espace des fonctions à valeur complexe de carré intégrable L2 :
et par généralisation à deux fonctions Φ (t, ... ) et Ψ (t, ... ) :
noté en mécanique quantique : 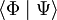 On identifie donc :
On identifie donc :
- la fonction Ψ (t, x, y, z, σ, ... ) avec un vecteur formel
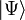 dénommé ket Ψ.
dénommé ket Ψ. - la fonctionnelle duale
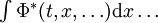 avec
avec 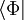 dénommé bra Φ, dual du ket Φ.
dénommé bra Φ, dual du ket Φ.
D'autre part sous le formalisme de Heisenberg, les solutions ne sont plus des fonctions, mais les vecteurs d'un espace de vecteurs d'états, ce qui rend l'identification toujours plus directe.
Soit un vecteur de l'espace des états. Il est noté 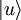 et se nomme vecteur-ket ou ket.
et se nomme vecteur-ket ou ket.
Deux kets forment un espace vectoriel linéaire. Ainsi, si λ1 et λ2 sont des nombres complexes quelconques et u1 et u2 sont deux kets :
alors v est un ket.
En allant plus loin, si 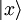 dépend d'un indice continu x, et si f est une fonction complexe normalisée sur
dépend d'un indice continu x, et si f est une fonction complexe normalisée sur ![[x_1\, ,x_2]](illustrations/2514f73230102db2fdc7528dc9dc8ed8.png) , alors,
, alors,
est un ket.
Propriétés
Le produit scalaire de deux kets est un nombre complexe, noté 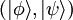 ou plus simplement
ou plus simplement 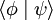 (voir plus bas : bra). Comme tout produit scalaire complexe, ce produit est sesquilinéaire (voir forme sesquilinéaire), c'est-à-dire que :
(voir plus bas : bra). Comme tout produit scalaire complexe, ce produit est sesquilinéaire (voir forme sesquilinéaire), c'est-à-dire que :
mais que :
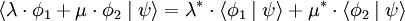 .
.
(l'expression c * veut dire qu'on prend le complexe conjugué de c — voir Nombre complexe)
Ce choix permet la définition d'une norme, qui est positive dans l'espace scalaire des nombres complexes. En effet, le produit scalaire d'un vecteur par lui-même est identique au carré de sa norme :
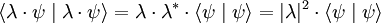 ,
,
avec λ un scalaire une sorte de facteur d'échelle. Et d'où :
Base et composantes
Il est commode d'utiliser une base pour définir les composantes d'un ket. C'est un ensemble de vecteurs 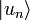 , linéairement indépendants. Il y a tout autant de vecteurs que de dimensions dans l'espace des états
, linéairement indépendants. Il y a tout autant de vecteurs que de dimensions dans l'espace des états 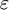 , et
, et 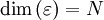 .
.
Ainsi, on peut décomposer 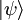 dans la base des
dans la base des 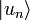 :
:
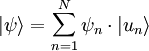 ,
,
où ψn sont les composantes de 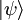 et appartiennent aux nombres complexes.
et appartiennent aux nombres complexes.
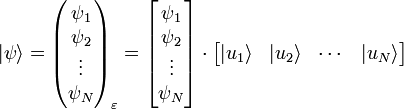
On représente le plus souvent un ket comme un vecteur colonne, une suite de nombres (les composantes) rangés verticalement :
On associe à chaque ket d'un espace 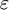 , un nombre complexe. On définit pour cela une fonctionnelle linéaire χ, telle que :
, un nombre complexe. On définit pour cela une fonctionnelle linéaire χ, telle que :
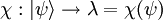 , et
, et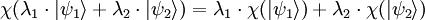
La totalité de ces fonctionnelles linéaires forme un espace vectoriel 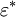 , dit «espace dual de
, dit «espace dual de 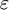 ». On nomme vecteur-bra ou bra un élément de cet ensemble et on le note
». On nomme vecteur-bra ou bra un élément de cet ensemble et on le note 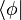 .
.
Ainsi, lorsque la fonctionnelle linéaire χ agit sur 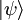 , on obtient :
, on obtient :
Cette nouvelle notation souligne la relation qu'il existe entre bra, ket et le produit scalaire entre kets. Prenons un ket 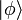 . Son produit scalaire avec
. Son produit scalaire avec 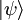 donne un nombre λ. On a ainsi défini une fonctionnelle linéaire qui, à
donne un nombre λ. On a ainsi défini une fonctionnelle linéaire qui, à 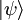 , fait correspondre un nombre complexe λ, à partir de
, fait correspondre un nombre complexe λ, à partir de 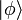 :
:
Puisque cette fonctionnelle se note 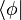 , on rédigé aussi :
, on rédigé aussi :
Ce qui amène à affirmer qu'à chaque ket correspond un bra, tel que le produit scalaire 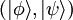 s'écrit
s'écrit 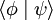 . Cette correspondance n'est cependant totalement pas réciproque. Il existe des bras qui n'ont aucun «équivalent ket» car ce sont des distributions.
. Cette correspondance n'est cependant totalement pas réciproque. Il existe des bras qui n'ont aucun «équivalent ket» car ce sont des distributions.
L'écriture 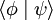 revêt alors deux significations, l'une étant le résultat de l'application d'une fonctionnelle à un ket, l'autre étant le produit scalaire de deux kets.
revêt alors deux significations, l'une étant le résultat de l'application d'une fonctionnelle à un ket, l'autre étant le produit scalaire de deux kets.
Propriétés
Il existe une correspondance entre bra et ket :
 (mais
(mais  n'est pas forcément vrai. )
n'est pas forcément vrai. )
L'antilinéarité du produit scalaire implique la correspondance suivante :
En effet, la norme de 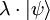 est définie positive :
est définie positive :
On identifie le ket 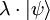 , ce qui implique que le «reste» de l'expression est le correspondant dans l'espace dual des fonctionnelles linéaires.
, ce qui implique que le «reste» de l'expression est le correspondant dans l'espace dual des fonctionnelles linéaires.
Composantes
L'écriture de la norme permet d'écrire un bra sous forme de composantes dans l'espace vectoriel dual 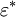 de même dimension que l'espace vectoriel
de même dimension que l'espace vectoriel 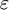 des états :
des états :
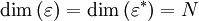 ,
, 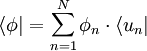 ,
, 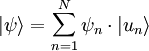 .
.
On représente aussi le bra sous la forme d'un vecteur ligne, une suite de nombres (les composantes) rangés horizontalement :
Le produit matriciel ci-dessus est commutatif, car la matrice ligne ne contient que des scalaires, la matrice colonne que des bras unitaires, et le produit d'un scalaire et d'un bra est commutatif, et le produit matriciel d'une matrice colonne et d'une matrice ligne, s'il est défini, est toujours commutatif. Il en est de même du produit matriciel d'une matrice colonne de scalaires et d'une matrice ligne de kets.
Il est alors envisageable d'écrire le produit scalaire d'un bra et d'un ket sous forme du produit de quatre matrices : deux matrices scalaires et des matrices de bras unitaires ou de kets unitaires. En permutant les matrices scalaires, il reste à déterminer le produit de matrices de bras unitaires et de kets unitaires. Or, ces matrices unitaires sont transposées et conjuguées, ce qui veut dire que leur produit se réduit au produit de leurs normes. Comme par définition, la norme des matrices unitaires est 1, ces matrices unitaires peuvent être éliminées du produit scalaire. La définition même du produit scalaire nous permet alors de l'écrire simplement en termes de produit de deux matrices scalaires de la façon suivante :
Opérateurs et notation de Dirac
D'une façon générale, les opérateurs linéaires agissant sur l'espace 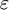 des états peuvent s'écrire sous la forme d'une combinaison linéaire d'opérateurs :
des états peuvent s'écrire sous la forme d'une combinaison linéaire d'opérateurs :
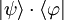 ,
,
dont l'action sur un état, représenté par le ket 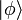 , sera l'état :
, sera l'état :
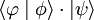 ,
,
donnant la possibilité une grande économie d'écriture.
Voir aussi
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

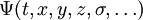
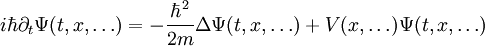
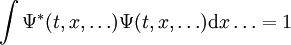
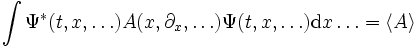
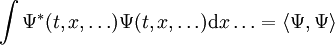
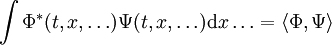
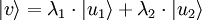
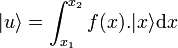
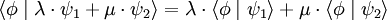
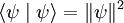
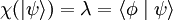
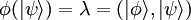
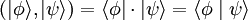
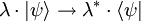
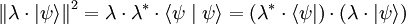
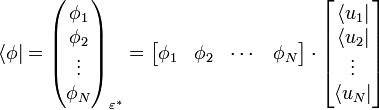
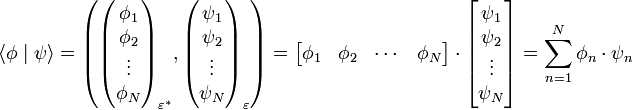

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité