Électrodynamique non linéaire de Born-Infeld
Théorie non linéaire développée par Born et Infeld dans les années 1930 pour supprimer le problème de l'énergie propre illimitée d'un électron existant dans la théorie linéaire de Maxwell.

Catégories :
Électromagnétisme - Électrodynamique quantique - Théorie quantique des champs - Physique quantique
Recherche sur Google Images :

Source image : fr.wikipedia.org Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- Le systèeme de Born - Infeld et sa version ´etendue non conservative Les champs de ..... [11] G. W. Gibbons & C. A. Herdeiro, Born - Infeld theory and stringy... (source : numdam)
Théorie non linéaire développée par Born et Infeld dans les années 1930 pour supprimer le problème de l'énergie propre illimitée d'un électron existant dans la théorie linéaire de Maxwell.
Ces auteurs espéraient résoudre ainsi le problème des illimités qui apparaissaient toujours dans la nouvelle électrodynamique quantique obtenue par la quantification canonique de la théorie de Maxwell.
Problème de l'énergie propre illimitée d'un électron
Supposons un électron sphérique de rayon a fixe en un point de l'espace, pris comme origine des coordonnées. Cet électron statique de charge 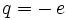 crée, dans la théorie linéaire de Maxwell, un champ coulombien dans l'espace environnant, qui vaut au point M repéré par le vecteur position
crée, dans la théorie linéaire de Maxwell, un champ coulombien dans l'espace environnant, qui vaut au point M repéré par le vecteur position 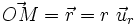 où
où 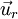 est le vecteur unitaire radial :
est le vecteur unitaire radial :
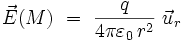 |
À ce champ électrique est associée, dans la théorie linéaire de Maxwell, la densité volumique d'énergie :
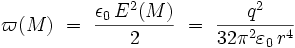 |
Calculons alors l'énergie totale dans l'espace entourant l'électron sphérique de rayon a ; il vient en coordonnées sphériques :
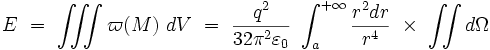 |
Sachant que l'intégrale angulaire vaut :
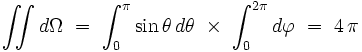 |
et que l'intégrale radiale vaut :
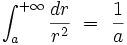 |
l'énergie totale dans l'espace entourant l'électron sphérique de rayon a vaut :
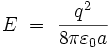 |
Cette expression diverge à la limite de l'électron ponctuel, où : 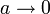 ! C'est pour éliminer ce problème que Born et Infeld ont développé une théorie non linéaire de l'électromagnétisme.
! C'est pour éliminer ce problème que Born et Infeld ont développé une théorie non linéaire de l'électromagnétisme.
Théorie de Born-Infeld
S'inspirant d'idées introduites par Mie en 1912-1913, Max Born va développer à partir de 1933 une théorie non linéaire de l'électrodynamique. Cette construction se fera rapidement en collaboration avec Infeld.
- Gustav Mie ; Grundlagen einer Theorie der Materie,
- Annalen der Physik 37 (1912) 511-534.
- Annalen der Physik 39 (1912) 1-40.
- Annalen der Physik 40 (1913) 1-66.
- Max Born ; Modified field equations with a finite radius of the electron, Nature 132 (1933) 282.
- Max Born & Leopold Infeld ; Electromagnetic mass, Nature 132 (1933) 970.
- Max Born & Leopold Infeld ; Foundation of the new field theory, Nature 132 (1933) 1004.
- Max Born & Leopold Infeld ; Foundation of the new field theory, Proceedings of the Royal Society London A 144 (1934) 425-451.
- Max Born & Leopold Infeld ; On the quantization of the new field equations,
- Part I : Proceedings of the Royal Society London A 147 (1934) 522-546.
- Part II : Proceedings of the Royal Society London A 150 (1935) 141-166.
- Max Born ; Théorie non-linéaire du champ électromagnétique, Annales de l'Institut Henri Poincaré 7 (1937) 155-265 (numérisé dans le cadre du programme NUMDAM).
Revues récentes
- Alexander A. Chernitskii ; Born-Infeld equations, Encyclopedia of Nonlinear Science, ed. Alwyn Scott. New York and London : Routledge (2004), pp. 67-69. Texte complet disponible sur l'ArXiv : hep-th/0509087.
- Michæl K. -H. Kiessling ; Electromagnetic field theory without divergence problems : 1. The Born Legacy, Journal of Statistical Physics vol. 116 (issue dedicated to Elliott H. Lieb on his 70th birthday). Texte complet disponible sur l'ArXiv : math-ph/0306076.
- Michæl K. -H. Kiessling ; Electromagnetic Field Theory without Divergence Problems 2. A Least Invasively Quantized Theory, Journal of Statistical Physics vol. 116 (issue dedicated to Elliott H. Lieb on his 70th birthday). Texte complet disponible sur l'ArXiv : math-ph/0311034.
- Mario Petropoulos ; L'action de Dirac-Born-Infeld : de l'électrodynamique non linéaire à la théorie M.
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 12/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité