Théorie de la fonctionnelle de la densité
La Théorie de la Fonctionnelle de la Densité ou DFT forme aujourd'hui l'une des méthodes les plus utilisées dans les calculs quantiques de la structure électronique de la matière autant en physique de la matière condensée qu'en chimie quantique.
Recherche sur Google Images :

Source image : www.plmc.univ-paris12.fr Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- L'objectif de cette théorie est de déterminer l'énergie totale d'un dispositif... La théorie de la fonctionnelle de la densité est basée sur le théorème de ... (source : yargla.labo.univ-poitiers)
- ... grande précision ; leur énergie et leurs proprié- tés physicochimiques sont aussi.... La théorie de la fonctionnelle de la densité est ... (source : cnrs)
- tron de cœur n'est plus négligeable devant l'énergie de masse E = mc..... type Kohn-Sham issus de la théorie de la fonctionnelle de la densité, est ... (source : springerlink)
| Méthodes numériques
pour le calcul de la structure électronique |
| Hartree-Fock |
| Théorie de la perturbation de Møller-Plesset |
| Interaction de configuration |
| Méthode du cluster couplé |
| Champ multi-configurationnel auto-cohérent |
| Théorie de la fonctionnelle de la densité |
La Théorie de la Fonctionnelle de la Densité ou DFT (pour Density Functional Theory) forme aujourd'hui l'une des méthodes les plus utilisées dans les calculs quantiques de la structure électronique de la matière (atomes, molécules, solides) autant en physique de la matière condensée qu'en chimie quantique. La DFT trouve ses origines dans le modèle développé par Llewellyn Thomas et Enrico Fermi à la fin des années 1920. Néanmoins il faudra attendre le milieu des années 1960 et les contributions de Pierre Hohenberg, Walter Kohn et Lu Sham pour que soit établi le formalisme théorique sur lequel repose la méthode actuelle.
Les méthodes respectant les traditions dans les théories de la structure électronique de la matière, surtout la théorie Hartree-Fock et les méthodes dérivées de ce formalisme, se fondent sur une fonction d'onde multiélectronique. L'objectif principal de la théorie de la fonctionnelle de la densité est de remplacer la fonction d'onde multiélectronique par la densité électronique comme quantité de base pour les calculs. Tandis que la fonction d'onde multiélectronique dépend de 3N variables (ou N est le nombre total de particules du dispositif), la densité est uniquement fonction de trois variables; il s'agit par conséquent d'une quantité plus facile à traiter tant mathématiquement que conceptuellement. Le principe de la DFT consiste en une reformulation du problème quantique à N corps en un problème monocorps (ou, à la rigueur, bi-corps si on considère les problèmes de spin) avec pour paramètre la densité électronique. L'idée centrale de la DFT est que l'unique densité électronique de l'état essentiel du dispositif détermine entièrement les valeurs moyennes des observables comme par exemple l'énergie.
La théorie DFT a été à l'origine essentiellement développée dans le cadre de la théorie quantique non-relativiste (équation de Schrödinger indépendante du temps) et dans l'approximation de Born-Oppenheimer. La théorie fut ensuite étendue au domaine de la mécanique quantique dépendante du temps (on parle alors de TDDFT pour Time-Dependent Density Functional Theory) et au domaine relativiste. La DFT est aussi utilisée pour la description thermodynamique des fluides classiques.
En 1998, Walter Khon (1923-) fut récompensé du prix Nobel de Chimie pour «son développement de la Théorie de la Fonctionnelle de la Densité»[1].
Notions de base
«Les lois physiques principales nécessaires à la théorie mathématique d'une grande partie de la physique et de la totalité de la chimie sont ainsi totalement connues, et la difficulté est uniquement que l'application exacte de ces lois mène à des équations énormément trop complexes pour être résolues»
— Paul A. M. Dirac, 1929[2]
Equation de Schrödinger
L'équation principale à résoudre pour décrire la structure électronique d'un dispositif à plusieurs noyaux et électrons est l'équation établie par Erwin Schrödinger (1887-1961) en 1925[3], nommée depuis équation de Schrödinger, et qui s'écrit[4] :
![H\Psi = \left[- \sum_iˆN \frac{\hbarˆ2}{2m}\nabla_iˆ2 - \sum_{I}ˆA \frac{\hbarˆ2}{2M}\nabla_Iˆ2 - \sum_{i,I} \frac{Z_I eˆ2}{|\vec r_i - \vec R_I|} + \frac{1}{2} \sum_{i<j} \frac{eˆ2}{|\vec r_i - \vec r_j|} + \frac{1}{2} \sum_{I<J} \frac{Z_I Z_J eˆ2}{|\vec R_I - \vec R_J|}\right] \Psi= E\Psi](illustrations/b55c82a596eae29e17cbea21f84d1188.png)
où 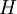 est l'hamiltonien moléculaire et
est l'hamiltonien moléculaire et 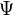 la fonction d'onde. Les deux premiers termes de l'hamiltonien sont respectivement les opérateurs énergie cinétique des
la fonction d'onde. Les deux premiers termes de l'hamiltonien sont respectivement les opérateurs énergie cinétique des 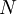 électrons (indexés
électrons (indexés 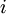 ) et des
) et des 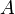 noyaux atomiques (indexés
noyaux atomiques (indexés 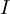 ). Les trois autres termes représentent les différents potentiels d'interaction électron-noyau, électron-électron et noyau-noyau.
). Les trois autres termes représentent les différents potentiels d'interaction électron-noyau, électron-électron et noyau-noyau.
Sous cette forme, l'équation de Schrödinger est trop complexe pour pouvoir être résolue analytiquement. De façon à simplifier la résolution de cette équation, Max Born (1882-1970) et Robert Oppenheimer (1904-1967) ont proposé une approximation visant à simplifier l'équation de Schrödinger[5]. L'approximation de Born-Oppenheimer considère la position des noyaux atomiques comme fixes ; leur énergie cinétique peut par conséquent être négligée et le terme d'interaction entre noyaux reconnu comme une constante (que on notera 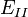 ). Cette approximation se justifie par le rapport de masse entre les particules constitutives du noyau (protons et neutrons) et les électrons[6]. L'équation à résoudre s'écrit alors :
). Cette approximation se justifie par le rapport de masse entre les particules constitutives du noyau (protons et neutrons) et les électrons[6]. L'équation à résoudre s'écrit alors :
![H\Psi = \left[- \sum_iˆN \frac{\hbarˆ2}{2m}\nabla_iˆ2 - \sum_{i,I} \frac{Z_I eˆ2}{|\vec r_i - \vec R_I|} + \frac{1}{2} \sum_{i<j} \frac{eˆ2}{|\vec r_i - \vec r_j|} + E_{II}\right] \Psi= E\Psi](illustrations/91861b4716441f08433e60f10d871618.png)
De manière à alléger les notations, on représentera, par convention, l'opérateur énergie cinétique par 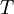 , le potentiel externe ressenti par les électrons par
, le potentiel externe ressenti par les électrons par 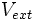 et le potentiel d'interaction électron-électron par
et le potentiel d'interaction électron-électron par 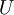 . L'équation s'écrit par conséquent sous une forme plus condensée comme[7] :
. L'équation s'écrit par conséquent sous une forme plus condensée comme[7] :
![\,\! H\Psi = [T + V_{ext} + U]\Psi = E\Psi](illustrations/fb608fc81b50578bf864736cee1bbd1d.png)
De nombreuses méthodes ont été développées pour résoudre l'équation de Schrödinger multiélectronique en décrivant par exemple la fonction d'onde comme un déterminant de Slater; c'est le cas de la méthode Hartree-Fock. La DFT apporte une méthode alternative en considérant comme quantité de base pour la description du dispositif la densité électronique.
La probabilité de trouver un électron parmi les 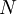 électrons du dispositif dans un élément de volume
électrons du dispositif dans un élément de volume 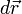 centré sur la position
centré sur la position 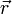 s'exprime comme :
s'exprime comme :
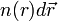
où 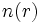 est la densité de probabilité électronique qui est définie comme[8] :
est la densité de probabilité électronique qui est définie comme[8] :
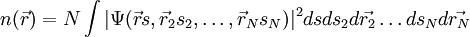
La densité de probabilité possède surtout deux propriétés importantes :
Densité de paire
La densité de paire est la probabilité de trouver simultanément 2 des N électrons du dispositif dans les éléments de volume 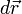 et
et 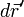 et est notée
et est notée 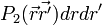
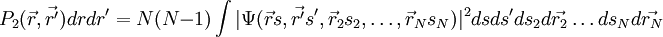
Modèle de Thomas-Fermi
La Théorie de la Fonctionnelle de la Densité tire ses origines du modèle de Thomas-Fermi, développé par Llewellyn Thomas <small> (1903-1992) </small> [9] et Enrico Fermi (1901-1954) [10] en 1927. La méthode de Thomas-Fermi repose sur un modèle statistique afin d'approximer la distribution électronique autour d'un atome. La base mathématique utilisée était de postuler que les électrons sont distribués du manière uniforme dans l'espace des phases, avec deux électrons dans chaque h3 de volume[11]. Pour chaque élément de coordonnées de l'espace volumique d3r il est envisageable de remplir une sphère d'espace de mouvement jusqu'au mouvement de Fermi pf[12].
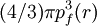
La mise en équation du nombre d'électrons en coordonnées spatiales dans cet espace des phases donne :
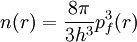
La résolution de cette équation pour pf et sa substitution dans la formule de l'énergie cinétique classique conduit directement à l'obtention d'une énergie cinétique, représentée comme une fonctionnelle de la densité électronique :
![T_{TF}[n]=\frac{3}{10}(3\piˆ2)ˆ{2/3}\int nˆ{5/3}(r) dˆ3r.](illustrations/fd5926f8552fdc84425a8ba70a05d01b.png)
De cette manière, il leur a été envisageable de calculer l'énergie d'un atome, en utilisant cette fonctionnelle d'énergie cinétique combinée avec l'expression classique des interactions noyau–électron et électron–électron qui peuvent eux aussi être exprimées en termes de densité électronique.
![E_{TF}[n]=\frac{3}{10}(3\piˆ2)ˆ{2/3}\int nˆ{5/3}(r) dˆ3r + \int{ V_{ext}(r)n(r)dr} + \frac{1}{2} \int{\frac{n(r)n(r')}{|r-r'|}drdr'}](illustrations/c800a2c9c1f7f97a783e9c0010d02f5b.png)
Bien que cela soit une importante première étape, la précision de l'équation de Thomas-Fermi reste cependant limitée, parce que la fonctionnelle de l'énergie cinétique résultante est approximée mais également parce que cette méthode ne tient pas compte de l'énergie d'échange d'un atome, conséquence du principe de Pauli, ni de la corrélation électronique. Une fonctionnelle d'échange énergétique fut ajoutée par Paul Dirac (1902-1984) en 1930[13].
Cependant, la méthode de Thomas-Fermi-Dirac reste assez imprécise pour la majorité des applications, la plus grande source d'erreur provenant de l'écriture de l'énergie cinétique qui peut cependant être perfectionnée en y ajoutant la correction proposée en 1935 par Carl von Weizsäcker (1912-2007) qui prend en compte le gradient de la densité dans l'expression de la fonctionnelle de l'énergie cinétique[14] :
![T_W[n]=\frac{1}{8}\frac{\hbarˆ2}{m}\int\frac{|\nabla n(r)|ˆ2}{n(r)}dr](illustrations/635a79018ee06cd0c59802c7b933ad76.png)
La methode de Thomas-Fermi a été surtout utilisée pour les équations d'états des éléments chimiques[15] mais sa portée ne peut être guère plus étendue. Edward Teller (1908-2003) a en effet montré en 1962 que la théorie de Thomas-Fermi était incapable de decrire la liaison moléculaire[16].
L'approche développée par Pierre Hohenberg et Walter Kohn est de reformuler la théorie de la fonctionnelle de la densité proposée par Thomas et Fermi par une théorie exacte d'un dispositif à plusieurs corps. La formulation est applicable pour tout dispositif de particules en interaction évoluant dans un potentiel externe et repose sur deux théorèmes essentiels qui furent énoncés et démontré par Hohenberg et Kohn dans leur article de 1964[17].
|
Le Premier Théorème HK peut se démontrer particulièrement simplement en utilisant un raisonnement par l'absurde. Supposons qu'il puisse exister deux potentiels externes différents 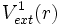 et
et 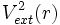 (par différent, on entend autrement que par une constante additive) associés à la densité de l'état essentiel
(par différent, on entend autrement que par une constante additive) associés à la densité de l'état essentiel 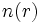 . Ces deux potentiels vont conduire à deux hamiltoniens différents
. Ces deux potentiels vont conduire à deux hamiltoniens différents 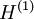 et
et 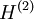 dont les fonctions d'ondes
dont les fonctions d'ondes 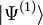 et
et 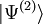 décrivant l'état essentiel sont différentes. Comme
décrivant l'état essentiel sont différentes. Comme 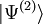 ne décrit par l'état essentiel de
ne décrit par l'état essentiel de 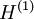 on peut par conséquent écrire que :
on peut par conséquent écrire que :
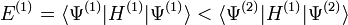
Cette inégalité stricte est valable si l'état essentiel est non dégénéré ce qui est supposé dans le cas de l'approche de HK. Le dernier terme de l'expression précédente peut s'écrire :
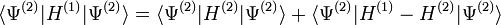
![= Eˆ{(2)}+ \int [V_{ext}ˆ1(r)-V_{ext}ˆ2(r)]n_0(r)dˆ3r](illustrations/18a84239a9168abcf6dc3a12f3291303.png)
ce qui donne :
![Eˆ{(1)}< Eˆ{(2)}+ \int [V_{ext}ˆ1(r)-V_{ext}ˆ2(r)]n_0(r)dˆ3r](illustrations/18ccd21ce6437563ae25f7cbc85f4908.png)
Il va aussi de soi que le même raisonnement peut être réalisé en considérant 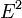 à la place de
à la place de 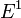 . On obtient alors la même équation que auparavant, les symboles (1) et (2) étant inversés :
. On obtient alors la même équation que auparavant, les symboles (1) et (2) étant inversés :
![Eˆ{(2)}< Eˆ{(1)}+ \int [V_{ext}ˆ2(r)-V_{ext}ˆ1(r)]n_0(r)dˆ3r](illustrations/ff5375f459594e68ea6208a4566c8371.png)
On additionnant membre à membre ces deux dernières équations, on obtient l'égalité contradictoire suivante :
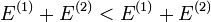
L'hypothèse de départ est par conséquent fausse; il ne peut exister deux potentiels externes différant par plus d'une constante conduisant à la même densité d'un état essentiel non dégénéré. Ceci achève la démonstration.
Le schéma ci-dessous illustre l'apport que apporte le premier théorème de Hohenberg et Khom. Les simples flèches indiquent le schéma obtenu dans le cas de la résolution traditionnelle de l'équation de Schrödinger où la connaissance du potentiel externe va permettre de déterminer les différents états électroniques (c'est-à-dire les fonctions d'ondes) mais aussi l'état essentiel et la densité électronique qui lui est associée. Le premier théorème HK, représenté par la double flèche, sert à compléter ce cycle. Cela veut dire que toutes les propriétés du dispositif peuvent être totalement déterminées si on connait la densité électronique de l'état essentiel.
![\begin{array}[t]{lcl} V_{ext}(r) &\Longleftarrow & n_0(r) \\
\downarrow & & \uparrow \\
\Psi_i({r}) & \rightarrow & \Psi_0({r})
\end{array}](illustrations/9ec96542bbe6e1c85d2140cc128be5de.png)
|
Toutes les propriétés du dispositif étant définies par la connaissance de la densité 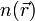 , elles peuvent par conséquent être décrites comme des fonctionnelles de la densité. L'énergie totale peut par conséquent s'écrire :
, elles peuvent par conséquent être décrites comme des fonctionnelles de la densité. L'énergie totale peut par conséquent s'écrire :
![E_{HK}[n]=T[n]+ U[n]+ \int V_{ext}(\vec r)n(\vec r) dˆ3r + E_{II}](illustrations/47ce660b8d1985ecf51d1c4d258ffe0c.png)
![= F_{HK}[n]+\int V_{ext}(\vec r)n(\vec r) dˆ3r + E_{II}](illustrations/4a1003e71bc96f5b72e8f2a66c63ee0e.png)
où 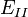 exprime l'énergie d'interaction entre les noyaux atomiques alors que la fonctionnelle
exprime l'énergie d'interaction entre les noyaux atomiques alors que la fonctionnelle ![\,\! F_{HK}[n]](illustrations/c5df61846ac602e226d6a35e8fbbcea6.png) inclut l'ensemble des contributions électroniques (énergies cinétique et potentielle). Cette fonctionnelle étant la même pour tout dispositif électronique (et indépendante du potentiel externe), elle est nommée fonctionnelle universelle.
inclut l'ensemble des contributions électroniques (énergies cinétique et potentielle). Cette fonctionnelle étant la même pour tout dispositif électronique (et indépendante du potentiel externe), elle est nommée fonctionnelle universelle.
![\,\! F_{HK}[n] = T[n]+ U[n]](illustrations/750787b0889c3789eb147cad92dfc02a.png)
Considérons désormais un dispositif ayant une densité à l'état essentiel noté 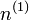 et qui correspond à un potentiel externe
et qui correspond à un potentiel externe 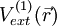 . La fonctionnelle de Hohenberg et Kohn est identique à la valeur obtenue pour l'hamiltonien de l'état essentiel associé à la fonction d'onde
. La fonctionnelle de Hohenberg et Kohn est identique à la valeur obtenue pour l'hamiltonien de l'état essentiel associé à la fonction d'onde 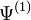 :
:
![Eˆ{(1)} = F_{HK}[nˆ{(1)}] = \langle \Psiˆ{(1)}|Hˆ{(1)}|\Psiˆ{(1)}\rangle](illustrations/ad18071706508e1530e89a468ece548c.png)
Si nous considérons désormais une densité différente 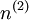 qui correspond obligatoirement à une fonction d'onde
qui correspond obligatoirement à une fonction d'onde 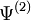 différente de
différente de 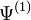 . On constate de manière immédiate que l'énergie
. On constate de manière immédiate que l'énergie 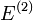 caractérisant cet état est plus élevée que
caractérisant cet état est plus élevée que 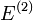 (l'état 1 est l'état essentiel et est unique par hypothèse).
(l'état 1 est l'état essentiel et est unique par hypothèse).
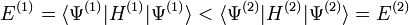
Par conséquence, la valeur de la fonctionnelle énergie de Hohenberg et Kohn évaluée pour la densité de l'état essentiel 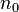 est nécessairement moindre que la valeur obtenue avec n'importe quelle autre densité
est nécessairement moindre que la valeur obtenue avec n'importe quelle autre densité 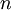 . Par conséquent on peut en déduire que, si la fonctionnelle universelle
. Par conséquent on peut en déduire que, si la fonctionnelle universelle ![\,\! F_{HK}[n]](illustrations/c5df61846ac602e226d6a35e8fbbcea6.png) est connue, la minimisation de l'énergie totale par une variation de la fonction densité va nous conduire à la densité (et par conséquent l'énergie) de l'état essentiel.
est connue, la minimisation de l'énergie totale par une variation de la fonction densité va nous conduire à la densité (et par conséquent l'énergie) de l'état essentiel.
Le second théorème montre que l'énergie apparaît comme une fonctionnelle de la densité, et que pour tout potentiel extérieur, la densité qui minimise cette fonctionnelle est la densité exacte de l'état essentiel.
En conclusion, les deux théorèmes proposés par Hohenberg et Kohn permettent de déplacer le problème posé par la résolution d'une équation de Schrödinger multiélectronique. En effet, la méthode DFT nous enseigne que si la forme de la fonctionnelle est connue, il est assez aisé, pour un potentiel externe donné, de déterminer l'énergie de l'état essentiel. Le problème qui se pose est alors la formulation de la fonctionnelle ![\,\! F[n]](illustrations/84c035108cf511edb68e07f4b3c0c829.png) et surtout l'expression de l'énergie cinétique
et surtout l'expression de l'énergie cinétique ![\,\! T[n]](illustrations/2220bca035dc1ca4b3c43a0465cf7de4.png) . En effet, il n'est pas envisageable, pour un dispositif de N électrons en interaction, de trouver une expression analytique à la fonctionnelle de l'énergie cinétique.
. En effet, il n'est pas envisageable, pour un dispositif de N électrons en interaction, de trouver une expression analytique à la fonctionnelle de l'énergie cinétique.
Ansatz de Kohn et Sham
«Si vous n'aimez pas la réponse, modifiez la question.»
— [18]
L'énergie cinétique d'un gaz d'électrons en interaction étant inconnue, Walter Kohn (1923-) et Lu Sham ont proposé en 1965 un ansatz qui consiste à remplacer le dispositif d'électrons en interaction, impossible à résoudre analytiquement, par un problème d'électrons indépendants évoluant dans un potentiel externe[19].
Mathématiquement, cela revient à exprimer la fonctionnelle énergie totale de Hohenberg et Kohn décrite comme :
![E_{HK}[n] = F[n] + \int V(r)n(r)dr](illustrations/472cb33d0bdcd630ae43055aaaf3c7ce.png)
par l'expression suivante :
![\,\! E_{S}[n] = T_{S}[n] + V_{S}](illustrations/9578633f5d77d53caeaf7dbc2b736670.png)
où ![\,\! T_{S}[n]](illustrations/f147bbb38e56b65ba9f257d99d510a2c.png) est l'énergie cinétique des électrons sans interaction et
est l'énergie cinétique des électrons sans interaction et ![\,\! V_{S}[n]](illustrations/832fa6ccda8cdadf2eadcd71a1a10de1.png) le potentiel dans lequel les électrons se déplacent. La densité électronique
le potentiel dans lequel les électrons se déplacent. La densité électronique 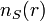 est strictement identique à la densité apparaissant dans la fonctionnelle définie par Hohenberg et Khon si le potentiel externe
est strictement identique à la densité apparaissant dans la fonctionnelle définie par Hohenberg et Khon si le potentiel externe ![\,\! V_{S}[n]](illustrations/832fa6ccda8cdadf2eadcd71a1a10de1.png) est défini comme :
est défini comme :
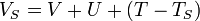
C'est-à-dire si ce dernier inclut la correction à l'énergie cinétique suite à l'ansatz de Khon et Sham. L'intérêt de la reformulation introduite par Khon et Sham est qu'on peut désormais définir un hamiltonien monoélectronique et écrire les équations de Khon-Sham monoélectroniques qui, au contraire de l'équation de Schrödinger définie plus haut, peuvent être résolues analytiquement.
![\left[-\frac{\hbarˆ2}{2m}\nablaˆ2+V_s(\vec r)\right] \phi_i(\vec r) = \epsilon_i \phi_i(\vec r),](illustrations/c9a797a1b4d0b830dd45383af75b9142.png)
La résolution des équations de Khon-Sham va permettre de déterminer les orbitales 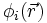 qui vont reproduire la densité électronique du dispositif multiélectronique d'origine.
qui vont reproduire la densité électronique du dispositif multiélectronique d'origine.
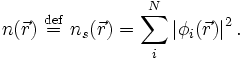
Le potentiel effectif monoélectronique apparaissant dans l'équation peut être exprimé de manière plus détaillée comme :
![V_s = V + \int \frac{n_s(\vec r\,) n_s(\vec r\,')}{|\vec r-\vec r\,'|} {\rm d}ˆ3r' + V_{\rm XC}[n_s(\vec r)]](illustrations/c589775595ba81530854a16e9bc4cd61.png)
Le premier terme est le potentiel externe créé par les noyaux, le deuxième exprime l'interaction coulombienne classique entre paire d'électrons (et est aussi nommé potentiel Hartree). Le dernier terme est le potentiel d'échange-corrélation et contient, hormis l'échange et la corrélation électronique, les corrections à l'énergie cinétique. Celle-ci n'est pas connue précisément, le choix d'une fonction d'échange corrélation approximée forme l'un des principaux choix d'approximation en DFT dans l'approche Kohn-Sham.
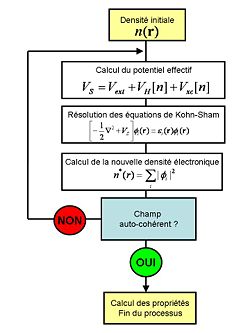
Comme on peut l'observer dans l'équation, ce potentiel dépend de la densité électronique, qui elle-même est calculée à partir des fonctions d'ondes des électrons indépendants, qui elle-même dépend du potentiel calculé à partir de la densité, etc. Cette approche conduit par conséquent à un traitement dit self-consistent field (ou méthode du champ auto-cohérent) : en partant d'une valeur arbitraire de départ, on calcule en boucle les valeurs de densité, potentiel et fonctions d'ondes jusqu'à une situation stable où ces différentes valeurs n'évoluent presque plus.
Résolution numérique des équations de K-S
L'ansatz de Kohn et Sham permet d'aboutir à un ensemble d'équations de Schrödinger monoélectroniques connues sous le nom d'équations de Kohn-Sham :
![\Big[ - \frac{\nablaˆ2}{2m} + V_{ext} + V_H + V_{xc} \Big]\phi_i = \epsilon_i \phi_i](illustrations/cdcae6cd76b92bd02b3bcfde7f4f76dc.png)
qui doivent être résolues numériquement selon un processus itératif. De façon à pouvoir résoudre ces équations de manière numérique, un certain nombre d'approximations peuvent ou doivent être envisagées. Klaus Capelle recense ainsi trois types d'approximations qui peuvent globalement être distinguées en DFT[20]. L'une est purement conceptuelle et concerne l'interprétation à donner aux valeurs propres 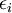 obtenues après résolution[21]. Il ne s'agit par conséquent pas précisément d'une approximation mais plutôt d'une réflexion sur la signification physique des valeurs propres. Le deuxième type d'approximation est d'ordre "technique" et concerne les choix effectués pour simplifier la résolution des équations; il s'agit essentiellement du choix des fonctions de bases et de la réduction du nombre d'électrons à prendre en considération dans les calculs (c'est-à-dire l'utilisation de pseudopotentiel). Ces deux approches seront brièvement décrites ci-dessous.
obtenues après résolution[21]. Il ne s'agit par conséquent pas précisément d'une approximation mais plutôt d'une réflexion sur la signification physique des valeurs propres. Le deuxième type d'approximation est d'ordre "technique" et concerne les choix effectués pour simplifier la résolution des équations; il s'agit essentiellement du choix des fonctions de bases et de la réduction du nombre d'électrons à prendre en considération dans les calculs (c'est-à-dire l'utilisation de pseudopotentiel). Ces deux approches seront brièvement décrites ci-dessous.
Approximations
Comme décrit plus haut la théorie DFT est , au stade des équations de Khon-Sham, une théorie idéalement exacte (mises à part l'approximation de Born-Oppenheimer et les approches numériques discutées auparavant) dans la mesure ou la densité électronique qui minimise l'énergie totale est précisément la densité du dispositif de N électrons en interaction. Cependant, la DFT reste inapplicable car le potentiel d'échange-corrélation (contenant aussi la correction à l'énergie cinétique) reste inconnu. Il est par conséquent indispensable d'approximer ce potentiel d'échange-corrélation. Deux types d'approximations existent : l'approximation de la densité locale ou LDA et l'approximation du gradient généralisé ou GGA mais aussi les méthodes dérivées qui se fondent sur une approche non locale.
LDA ou approximation de la densité locale
L'approche de la densité locale est fondée sur le modèle du gaz uniforme d'électron et forme l'approche la plus simple pour exprimer l'énergie d'échange-corrélation. Celle-ci est décrite comme :
![E_{xc}[n] = \int n(\vec r)\varepsilon _{xc}[n]dr](illustrations/c20374d8eba6d31b056b47a30b7df39c.png)
où ![\varepsilon _{xc}[n]](illustrations/13311151c3a3d599227cb21ea44f7acd.png) sert à désigner l'énergie d'échange-corrélation pour une particule d'un gaz homogène d'électron. La fonction
sert à désigner l'énergie d'échange-corrélation pour une particule d'un gaz homogène d'électron. La fonction ![\varepsilon _{xc}[n]](illustrations/13311151c3a3d599227cb21ea44f7acd.png) peut être décomposée en une contribution d'échange
peut être décomposée en une contribution d'échange ![\varepsilon _x[n]](illustrations/4e09cbdeaacc049a30c9bea61d6d0ada.png) et de corrélation
et de corrélation ![\varepsilon _c[n]](illustrations/cab2302f04056f5fc9ad6f41ab9b95e6.png) [22] :
[22] :
![\varepsilon _{xc}[n] = \varepsilon _x[n] + \varepsilon _c[n]](illustrations/4a901a3658a1a5a87460e695472f1b07.png)
La contribution provenant de l'échange électronique dans l'approximation de la densité locale est connue et provient de la fonctionnelle d'énergie d'échange formulée par Dirac [23]
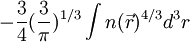
L'approximation LDA peut être formulée de manière plus générale en prenant en compte le spin de l'électron dans l'expression de la fonctionnelle, on parle alors d'approximation LSDA (pour local spin density approximation). Cette approche fut originellement proposée par John C. Slater (1900-1976) [24] et sert à résoudre certains problèmes liés à une approche LDA, surtout le traitement de dispositifs soumis à des champs magnétiques et les dispositifs où les effets relativistes deviennent importants. En prenant en compte l'approximation LSDA, la fonctionnelle d'échange est exprimée comme :
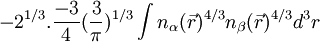
où α et β expriment les spins up et down[25].
Pour l'énergie de corrélation, des valeurs précises sont disponibles via les calculs de Monte Carlo quantique établi par Ceperley[26]et par Ceperley et Alder[27] dont les résultats peuvent être interpolés afin d'obtenir une forme analytique. Il existe par conséquent de nombreuses paramétrisations pour l'énergie de corrélation telles que, par exemple, celles de Hedin-Lundqvist [28], Perdew-Zunger[29] ou Volko-Wilkes-Nusair[30]
Dans l'approximation LDA (ou LSDA), le potentiel de corrélation est défini par[31] :
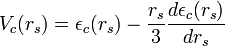
où 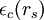 est l'énergie de corrélation et
est l'énergie de corrélation et 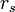 un paramètre qui décrit le rayon d'une sphère contenant en moyenne un électron dans un dispositif électronique homogène de densité
un paramètre qui décrit le rayon d'une sphère contenant en moyenne un électron dans un dispositif électronique homogène de densité 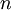 [32].
[32].
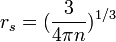
- Forme de Hedin-Lundqvist[33]
![\epsilon_c(r_s)ˆ{HL} = - \frac{Ceˆ2}{2}\Big[(1+xˆ3)log(1+\frac{1}{x})+\frac{x}{2}-xˆ2-\frac{1}{3}\Big]](illustrations/d43991d977e42029eea9b4c3e7064994.png)
où A = 21, C = 0.045 et x = rs/A
![V_c(r_s)ˆ{HL} = - \frac{Ceˆ2}{2}log\Big[1+\frac{1}{x}\Big]](illustrations/0c3bcc3a23be79da12d4b0711053eb99.png)
«L'approximation LSD est ainsi une approximation "first-principle", dans le sens où ses paramètres ne sont pas interpolés empiriquement à des résultats calculés ou expérimentaux autres que ceux pour lesquels sa forme est exacte.»
— J. Perdew et al (1996) [34]
Quoiqu'étant une approche assez simple conceptuellement, l'approximation LDA permet néanmoins d'obtenir de bons résultats. Une compensation des erreurs permet d'expliquer en partie le relatif succès de la méthode LDA. Celle-ci tend en effet à sous-estimer l'énergie d'échange tandis qu'elle surestime l'énergie de corrélation ce qui permet, in fine d'obtenir des valeurs assez bonnes pour l'énergie d'échange-corrélation.
GGA ou approximation des gradients généralisée
L'approche LDA se fondait sur le modèle du gaz d'électrons et supposait par conséquent une densité électronique uniforme. Cependant les dispositifs atomiques ou moléculaires sont le plus fréquemment particulièrement différents d'un gaz d'électrons homogène et , de manière plus générale, on considère généralement que l'ensemble des dispositifs réels sont inhomogènes c'est-à-dire que la densité électronique possède une variation spatiale. Les méthodes dites GGA (Generalized gradient approximation), quelquefois aussi nommées méthodes non locales, ont été développées de façon à prendre en compte cette variation de la densité en exprimant les énergies d'échanges et de corrélation selon la densité mais également de son gradient (c'est-à-dire sa dérivée première). Généralement, l'énergie d'échange-corrélation est définie dans l'approximation GGA comme :
![E_{xc}ˆ{GGA}[n_{\alpha}, n_{\beta}] = \int n(\vec r) \epsilon_{xc}[n_{\alpha}, n_{\beta}, \nabla n_{\alpha}, \nabla n_{\beta}] dˆ3r](illustrations/2702d7fb309653f5dac2fdec182d10fa.png)
Globalement, les fonctionnelles GGA sont construites selon deux types de procédures différents. L'un est de nature empirique et consiste en une interpolation numérique des résultats expérimentaux obtenus sur la plupart de molécules. On peut citer comme exemple de fonctionnelle construite selon ce processus les fonctionnelles d'échange notée B (Becke88) [35], PW (Perdew-Wang) [36] ou bien toujours mPW (modified Perdew-Wang) [37]. La seconde procédure consiste à construire les fonctionnelles sur la base des principes de la mécanique quantique (et est en ce sens plus rationnelle). Les fonctionnelles d'échange B88 (Becke88) [38], P (Perdew86) [39] ou PBE (Perdew-Burke-Ernzerhof) [40] sont construites de cette manière.
Dans l'approximation GGA, la fonctionnelle d'échange est exprimée comme[41] :
![E_xˆ{GGA}[n] = \int n(r) \epsilon_xˆ{hom.}[n(r)]f(\zeta)dˆ3r](illustrations/87fc4b6c6c45239fb174211a9ab6ea6f.png)
où 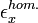 est l'énergie d'échange pour un gaz homogène d'électrons et
est l'énergie d'échange pour un gaz homogène d'électrons et 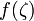 un facteur d'amélioration (en anglais enhancement factor) avec
un facteur d'amélioration (en anglais enhancement factor) avec 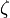 la variable sans dimension
la variable sans dimension
![\zeta = \frac{|\nabla n|ˆ2}{[2(3\piˆ2)ˆ{1/3}]ˆ2 nˆ{5/3}}](illustrations/be649c5328debde344c34bbcbebe7c69.png)
Au-delà de GGA, l'échelle de Jacob
Les méthodes GGA permettent d'obtenir un progrès des résultats comparé à une approche locale. Cependant, comme décrit plus haut, l'approche GGA n'est pas forcément suffisante pour une description correcte de diverses propriétés chimiques des composés. C'est pourquoi, à partir du milieu des années 1990, de nouveaux types de fonctionnelles ont été développées de façon à aller au-delà des résultats apportés par des méthodes GGA. Les fonctionnelles dites meta-GGA (ou m-GGA) font ainsi intervenir dans les équations le laplacien (c'est-à-dire la dérivée seconde) de la densité. Celles-ci permettent un gain de précision dans la détermination des propriétés moléculaires mais posent certains problèmes au niveau de la stabilité numérique. On peut citer comme exemple de fonctionnelle m-GGA, la fonctionnelle de corrélation B95 développée par Becke[42]. Un degré de précision supplémentaire est atteint en combinant l'échange et la corrélation obtenu par des méthodes GGA avec un certain pourcentage d'échange décrit par la théorie Hartree-Fock[43]. Les fonctionnelles construites sur ce principe sont qualifiées de fonctionnelles hybrides, on parle alors de fonctionnelles H-GGA (hybrid-GGA functional). La détermination du pourcentage d'échange Hartree-Fock à inclure dans la fonctionnelle est principalement déterminée de manière empirique. L'utilisation de ce type de fonctionnelle permet un progrès significative des résultats et est devenue depuis plusieurs années le choix le plus populaire dans le domaine de la chimie quantique. La fonctionnelle d'échange-corrélation hybride B3LYP représentait ainsi 80% d'utilisation sur la période 1990-2006[44]. Les fonctionnelles HM-GGA (Hybrid-Meta GGA functional) représentent une nouvelle classe de fonctionnelles et font aujourd'hui l'objet de nombreux développements. Le concept est comparable à l'approche des fonctionnelles hybrides, la différence est qu'on part de fonctionnelle m-GGA à la place de GGA. Ces fonctionnelles font par conséquent intervenir l'échange Hartree-Fock, la densité électronique et son gradient mais aussi la densité électronique de l'énergie cinétique (c'est-à-dire le laplacien de la densité). C'est la cas, par exemple, de la fonctionnelle B1B95[42].
«[Jacob] eut un songe. Et voici, une échelle était appuyée sur la terre, et son sommet touchait au ciel. Et voici, les anges de Dieu montaient et descendaient par cette échelle.»
— Gn 28. 12
La métaphore de l'échelle de Jacob est due à J. Perdew[45] et illustre le progrès croissant dans le domaine des fonctionnelles de la densité depuis le milieu des années 1980. L'échelle de Jacob qu'elle que vue par Perdew contient 5 échelons représentant les 5 générations de fonctionnelles. Les utilisateurs prennent ici la place des anges, montant ou descendant les barreaux selon ses besoins qui résultent d'un compromis entre exactitude et ressources informatiques disponibles.
| Paradis = exactitude | ||
| Echelon | Méthode | Exemple |
|---|---|---|
|
5e échelon |
Complètement non local |
- |
|
4e échelon |
Hybrid Meta GGA |
B1B95 |
|
Hybrid GGA |
B3LYP |
|
|
3e échelon |
Meta GGA |
BB95 |
|
2e échelon |
GGA |
BLYP |
|
1e échelon |
LDA |
SPWL |
|
Terre = Théorie Hartree-Fock |
||
Nomenclature des fonctionnelles : l'exemple de B3LYP
Les fonctionnelles d'échange et de corrélation peuvent adopter des formes mathématiques fréquemment complexes. De façon à simplifier les notations, la convention est de noter les fonctionnelles du nom de leur (s) auteur (s) suivi de la date de publication dans le cas ou un même groupe a publié plusieurs fonctionnelles différentes. La fonctionnelle d'échange électronique développée par Axel Becke en 1988 est ainsi notée B et la fonctionnelle de corrélation publiée par le même auteur en 1995 est notée B95. Dans le cas où plusieurs auteurs sont impliqués dans le développement, les initiales de ceux-ci sont utilisées pour symboliser la fonctionnelle. La fonctionnelle de corrélation LYP est ainsi appelée du nom de ses trois auteurs Lee, Yang et Parr.
La description complète de l'échange et de la corrélation électronique est obtenue en combinant une fonctionnelle d'échange et une fonctionnelle de corrélation. La fonctionnelle est alors symbolisée en ajoutant simplement les symboles des fonctionnelles d'échange et de corrélation (toujours dans cet ordre). Dans les cas plus complexe des fonctionnelles hybrides le nombre de paramètres impliqués est aussi mentionné.
B3LYP est aujourd'hui la fonctionnelle la plus employée en principe DFT. C'est une fonctionnelle hybride obtenue par combinaison linéaire entre des fonctionnelles d'échange et de corrélation GGA et de l'échange Hartree-Fock. B3LYP veut dire Becke - 3 paramètres - Lee, Yang, Parr et est décrite comme :
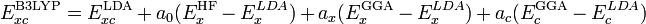
Principales fonctionnelles d'échange-corrélation
Le tableau ci-dessous renseigne les principales fonctionnelles d'échange-corrélation employées dans les calculs DFT classées selon le type d'approximation utilisé. Une description plus complète mais aussi les références relatives aux diverses fonctionnelles reprises dans le tableau peuvent être trouvée dans le review publié par S. F. Sousa et al. [44]
| Type | Fonctionnelle | Année | Fonctionnelle
d'échange |
Pourcentage
d'échange HF |
Fonctionnelle
de corrélation |
|---|---|---|---|---|---|
|
LSDA |
SVWN3 | 1981 | Slater | 0 | VWN n°3 |
| SVWN5 | 1981 | Slater | 0 | VWN n°5 | |
| SPWL | 1992 | Slater | 0 | Perdew Wang locale | |
|
GGA |
BLYP | 1988 | Becke88 | 0 | Lee-Yang-Parr |
| BP86 | 1988 | Becke88 | 0 | Perdew86 | |
| BPW91 | 1991 | Becke88 | 0 | Perdew-Wang 91 | |
| PBE | 1996 | Perdew-Burke-Ernzerhof | 0 | Perdew-Burke-Ernzerhof | |
| BPBE | 1996 | Becke88 | 0 | Perdew-Burke-Ernzerhof | |
| G96LYP | 1996 | Gill96 | 0 | Lee-Yang-Parr | |
| HCTH | 1998 | Hamprecht-Cohen-Tozer-Handy | 0 | Hamprecht-Cohen-Tozer-Handy | |
| mPWLYP | 1998 | modified Perdew-Wang91 | 0 | Lee-Yang-Parr | |
| mPWPW91 | 1998 | modified Perdew-Wang91 | 0 | Perdew-Wang91 | |
| XLYP | 2004 | Becke88 + Perdew-Wang91 | 0 | Lee-Yang-Parr | |
| MGGA | BB95 | 1996 | Becke88 | 0 | Becke95 |
| HGGA | B3LYP | 1994 | Becke88 | 20 | Lee-Yang-Parr |
| HMGGA | B1B95 | 1996 | Becke88 | 25 | Becke95 |
Une méthode ab initio ou semi-empirique?
Les méthodes basées sur la théorie de la fonctionnelle de la densité sont reconnues à l'heure comme une théorie ab initio par la majorité des scientifiques. En effet, les théorèmes de Hohenberg et Khon mais aussi le développement amenant aux équations monoélectroniques de Kohn et Sham sont idéalement rigoureux et sont obtenus sans avoir recours à d'éventuelles approximations. Cependant, la fonctionnelle d'échange-corrélation apparaissant dans les équations rend toutes résolutions exactes impossibles, sa forme analytique étant inconnue. Comme décrit plus haut, il est par conséquent indispensable d'approximer cette fonctionnelle soit en formulant une forme mathématique approchée de la fonctionnelle ou bien en fittant un certain nombre de données expérimentales. Cette approche est typique des méthodes semi-empiriques et la méthode DFT pourrait par conséquent tout autant être classée dans cette catégorie. L'énergie totale en DFT est exprimée en termes dépendant de la densité électronique plutôt qu'en termes de fonctions d'onde. Il est probablement plus pertinent de considérer la méthode DFT comme une classe à part dans les méthodes numériques de chimie quantique.
Bibliographie
![]() : source utilisée pour la rédaction de cet article
: source utilisée pour la rédaction de cet article
- (en) Robert G. Parr et Weitao Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, 1989, 350 p. (ISBN 0195092767)
- (en) Eberhard K. U. Gross et Reiner M. Dreizler, Density Functional Theory, Springer, 1995 (ISBN 0306449056)
- (en) Norman H. March, Electron Density Theory of Atoms and Molecules, Elsevier Science & Technology Books, 1997, 339 p. (ISBN 9780124705258)
- (en) Carlos Fiolhais, Fernando Nogueira et Miguel Marques, A primer in Density Functional Theory, Springer, 2003, 256 p. (ISBN 3540030832)
- (en) Richard M. Martin, Electronic Structure Basic Theory and Practical Methods, Cambridge University Press, 2004, 648 p. (ISBN 0521782856)

Notes et références
- ↑ (en) The Nobel Fundation, «The Nobel Prize of Chemistry 1998», 1998. Consulté le 24 février 2008
- ↑ (en) P. A. M. Dirac, «Quantum Mechanics of Many-Electron Systems», dans Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, vol. 123, no 792, 1929, p. 714-733 : The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble.
- ↑ (en) E. Schrödinger, «An Undulatory Theory of the Mechanics of Atoms and Molecules», dans Phys. Rev. , vol. 28, 1926, p. 1049-1070 [lien DOI]
- ↑ (fr) Il s'agit ici de l'équation de Schrödinger indépendante du temps.
- ↑ (de) M. Born et R. Oppenheimer, «Zur Quantentheorie der Molekeln», dans Annealen der Phyzik, vol. 389, 1927, p. 457-484 [lien DOI]
- ↑ (fr) La masse d'un nucléon est à peu près 1837 fois plus grande que la masse d'un électron
- ↑ (fr) Suite à l'approximation de Born-Oppenheimer, le hamiltonien total peut être scindé en un hamiltonien nucléaire et un hamiltonien électronique. Les propriétés des matériaux étant principalement caractérisées par le comportement des électrons, le hamiltonien décrit dans la suite de cet article sera toujours l'hamiltonien électronique.
- ↑ (fr) Par convention, la densité électronique est symbolisée par n (r) dans cet article. Il est cependant courant de la trouver symbolisée par ρ (r) dans de nombreux ouvrages et publications.
- ↑ (en) L. H. Thomas, «The calculation of atomic field», dans Proc. Cambridge Phil. Roy. Soc. , vol. 23, 1927, p. 542-548
- ↑ (it) E. fermi, «Un metodo statistico per la determinazione di alcune priorieta dell'atome», dans Rend. Accad. Naz. Lincei, vol. 6, 1927, p. 602-607
- ↑ (en) Robert G. Parr et Weitao Yang, op. cit. , 47
- ↑ (en) Norman H. March, op. cit, p. 24
- ↑ (en) P. A. M. Dirac, «Note on exchange phenomena in the Thomas-Fermi atom», dans Proc. Cambridge Phil. Roy. Soc. , vol. 26, 1930, p. 376-385
- ↑ (de) C. F. von Weizsacker, «Zur Theorie der Kernmassen», dans Z. Phys. , vol. 96, 1935, p. 431
- ↑ (en) R. P. Feynman, N. Metropolis et E. Teller, «Equations of state of elements based on the Thomas-Fermi theory», dans Phys. Rev. , vol. 75, 1949, p. 1561-1573 [lien DOI]
- ↑ (en) E. Teller, «On the stability of molecules in the Thomas-Fermi theory», dans Rev. Mod. Phys. , vol. 34, 1962, p. 627-630 [lien DOI]
- ↑ (en) P. Hohenberg et W. Kohn, «Inhomogenous Electron Gas», dans Phys. Rev. , vol. 136, 1964, p. B864-B871 [lien DOI]
- ↑ (en) Richard L. Martin, op. cit. p. 135 : If you don't like the answer, change the question
- ↑ (en) W. Khon, et L. J. Sham, «Self-Consistent Equations Including Exchange and Correlation Effects», dans Phys. Rev. , vol. 140, 1965, p. A1133-A1138 [lien DOI]
- ↑ (en) Klaus Capelle, «A bird's-eye view of density-functional theory. », dans Braz. J. Phys. , vol. 36, no 4A, 2006, p. 1318-1343 (ISSN 0103-9733)
- ↑ (fr) Au contraire de l'équation de Schrödinger, les valeurs propres des équations de Kohn-Sham ne représentent pas à proprement parler l'énergie.
- ↑ (fr) Quoiqu'il soit commun de séparer ainsi l'échange et la corrélation, il existe néanmoins quelques doutes sur la légitimité de cette séparation.
- ↑ (en) Richard L. Martin, op. cit. , p 120
- ↑ (en) J. C. Slater, «Simplification of the Hartree-Fock Method», dans Phys. Rev. , vol. 81, 1951, p. 385-390 [lien DOI]
- ↑ (fr) Dans le cas de dispositifs électroniques à couches fermées, la densité électronique des spin up et down sont identiques et les approches LDA et LSDA deviennent semblables
- ↑ (en) D. Ceperley, «Ground state of the fermion one-component plasma : A Monte Carlo study in two and three dimensions», dans Phys. Rev. B, vol. 18, 1978, p. 3126-3138 [lien DOI]
- ↑ (en) D. M. Ceperley et B. J. Alder, «Ground State of the Electron Gas by a Stochastic Method», dans Phys. Rev. Lett. , vol. 45, 1980, p. 566-569 [lien DOI]
- ↑ (en) R. L. Martin, op. cit. p. 479
- ↑ (en) J. P. Perdew and A. Zunger, «Self-interaction correction to density-functional approximations for many-electron systems», dans Phys. Rev. B, vol. 23, 1981, p. 5048-5079 [lien DOI]
- ↑ (en) S. H. Vosko, L. Wilk et M. Nusair, «Accurate spin-dependent electron liquid correlation energies for local spin density calculations : a critical analysis», dans Can. J. Phys, vol. 58, 1980, p. 1200-1211
- ↑ (en) Richard L. Martin, op. cit. , p. 479
- ↑ (en) Richard L. Martin, op. cit. , p. 100
- ↑ (en) Richard L. Martin, op. cit. , p. 479-480
- ↑ (en) Ref nécessaire : LSD is thus a first-principle approximation, in the sens that its parameters are not fitted empirically to calculated or experimentals results other than one in which its form is exact
- ↑ (en) A. D. Becke, «Density-functional exchange-energy approximation with correct asymptotic behavior», dans Phys. Rev. A, vol. 38, 1988, p. 3098 [lien DOI]
- ↑ (en) J. P. Perdew, K. Burke et Y. Wang, «Generalized gradient approximation for the exchange-correlation hole of a many-electron system», dans Phys. Rev. B, vol. 54, 1996, p. 16533-16539 [lien DOI]
- ↑ (en) C. Adamo et V. Barone, «Exchange functionals with improved long-range behavior and adiabatic connection methods without adjustable parameters : The mPW and mPW1PW models», dans J. Chem. Phys. , vol. 108, 1998, p. 664 [lien DOI]
- ↑ (en) A. D. Becke, «Density-functional exchange-energy approximation with correct asymptotic behavior», dans Phys. Rev. A, vol. 38, 1988, p. 3098-3100 [lien DOI]
- ↑ (en) J. P. Perdew et Y. Wang, «Accurate and simple density functional for the electronic exchange energy : Generalized gradient approximation», dans Phys. Rev. B, vol. 33, 1986, p. 8800-8802 [lien DOI]
- ↑ (en) J. P. Perdew, K. Burke, et M Ernzerhof, «Generalized Gradient Approximation Made Simple», dans Phys. Rev. Lett. , vol. 77, 1996, p. 3865-3868 [lien DOI]
- ↑ (en) Richard L. Martin op. cit. p 154-155
- ↑ a b (en) A. D. Becke, «Density-functional thermochemistry. IV. A new dynamical correlation functional and implications for exact-exchange mixing», dans J. Chem. Phys. , vol. 104, 1996, p. 1040 [lien DOI]
- ↑ (fr) Ce choix est fondé sur le fait que l'échange électronique est décrit de manière exacte dans la théorie Hartree-Fock
- ↑ a b (en) S. F. Sousa, P. A. Fernandes et M. J. Ramos, «General Performance of Density Functionals», dans J. Phys. Chem. A, vol. 111, 2007, p. 10439-10452 [lien DOI]
- ↑ (en) J. P. Perdew, K. Schmidt, Density Functional Theory and Its Application to Materials, V. Van Doren, C. Van Alsenoy, P. Geerlings, 1 août 2001, 220 p. (ISBN 9780735400160)
Voir aussi
Liens externes
- [pdf] Electronic structure of Matter - Wave functions and density functionals : Nobel Lecture de Walter Kohn sur la DFT
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

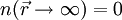
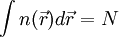


 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité