Coefficients de Clebsch-Gordan
En physique, les cœfficients de Clebsch-Gordan sont des nombres qui apparaissent lors de l'étude des couplages de moment angulaire soumis aux lois de la mécanique quantique.
En physique, les cœfficients de Clebsch-Gordan sont des nombres qui apparaissent lors de l'étude des couplages de moment angulaire soumis aux lois de la mécanique quantique. Ils portent le nom des mathématiciens allemands Alfred Clebsch (1833-1872) et Paul Gordan (1837-1912), qui rencontrèrent un problème identique en théorie des invariants.
En théorie de la représentation, surtout des groupes de Lie compacts, ces cœfficients sont utilisés pour effectuer la somme directe du produits tensoriels de deux représentations irréductibles.
On peut définir les cœfficients de Clebsch-Gordan associés au groupe SO (3) d'une manière plus directe, comme produit d'harmoniques sphériques. L'addition de spins en mécanique quantique se comprend par cette approche. Dans cet article, on utilisera la notation bra-ket de Dirac.
Les opérateurs de moment angulaire sont les opérateurs hermitiens j1, j2 et j3 qui vérifient les relations suivantes :
avec 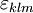 le symbole de Levi-Civita. Ces trois termes peuvent être reconnus comme les composantes d'un opérateur vectoriel
le symbole de Levi-Civita. Ces trois termes peuvent être reconnus comme les composantes d'un opérateur vectoriel 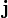 . Le carré de la norme de
. Le carré de la norme de 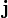 est défini par :
est défini par :
On définit aussi les opérateurs (j +) et (j −) par :
États de moment angulaire
On peut montrer que 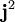 commute avec j1, j2 et j3 :
commute avec j1, j2 et j3 :
![\left[ \mathbf{j}ˆ2, j_k \right] = 0](illustrations/bc7437357f7e8ccd86b7f705a61bfcbb.png) avec k = 1, 2, 3.
avec k = 1, 2, 3.
Quand deux opérateurs hermitiens commutent, ils possèdent un ensemble commun de fonctions propres. Par convention, on choisit 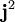 et j3. Selon les relations de commutation, on détermine les valeurs propres :
et j3. Selon les relations de commutation, on détermine les valeurs propres :
Les opérateurs (j +) et (j −) changent la valeur de m :
avec
Un facteur de déphasage (complexe) peut être ajouté à la définition de 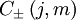 . Les états de moment angulaire doivent être orthogonaux — car leurs valeurs propres sont différentes — et sont supposés normalisés :
. Les états de moment angulaire doivent être orthogonaux — car leurs valeurs propres sont différentes — et sont supposés normalisés :
Les états de moment angulaire peuvent être développés en les supposant non-couplés :
Les cœfficients qui apparaissent dans le développement, notés 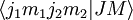 , sont les cœfficients de Clebsch-Gordan.
, sont les cœfficients de Clebsch-Gordan.
En appliquant l'opérateur :
des deux côtés de l'égalité, on montre que les cœfficients de Clebsch-Gordan peuvent ne pas être nuls uniquement lorsque :
Relations d'orthogonalité
On peut introduire la notation alternative, mais équivalente, suivante :
Il est alors envisageable d'établir deux relations d'orthogonalité :
Propriétés de symétrie
La relation de symétrie suivante est toujours valable :
Lien avec les symboles 3—jm
Les cœfficients de Clebsch-Gordan sont reliés aux symboles 3-jm, qui sont plus agréables à manipuler du fait de symétries plus simples. Cette relation s'exprime par l'équation suivante :
- (en) Cet article est partiellement ou en totalité issu d'une traduction de l'article de Wikipédia en anglais intitulé «Clebsch-Gordan cœfficients».
Liens externes
- (en) JavaTM Calcul des cœfficients de Clebsch-Gordan ;
- (en) Calculateur des cœfficients de Clebsch-Gordan, des cœfficients 3-j et 6-j.
Bibliographie
- C. Cohen-Tannoudji, B. Diu et F. Laloë, Mécanique quantique [détail des éditions]
- Albert Messiah, Mécanique quantique [détail des éditions]
- (en) Edmonds, A. R. : «Angular Momentum in Quantum Mechanics», Princeton University Press (1957). ISBN 0-691-07912-9.
- (en) Condon, Edward U., Shortley, G. H. : «The Theory of Atomic Spectra», Cambridge University Press (1970). ISBN 0-521-09209-4.
- (en) Brink, D. M., Satchler, G. R. : Angular Momentum, 3e édition, Clarendon Press (1993), Oxford. ISBN 0-19-851759-9.
- (en) Zare, Richard N. : Angular Momentum, John Wiley & Sons (1988), New York. ISBN 0-471-85892-7.
- (en) Biedenharn, L. C., Louck, J. D., Angular Momentum in Quantum Physics, Addison-Wesley (1981), Reading, Massachusetts. ISBN 0-201-13507-8.
Recherche sur Google Images : |
|
"Les coefficients de Clebsch-Gordan ..." L'image ci-contre est extraite du site reference.wolfram.com Il est possible que cette image soit réduite par rapport à l'originale. Elle est peut-être protégée par des droits d'auteur. Voir l'image en taille réelle (596 x 133 - 3 ko - gif)Refaire la recherche sur Google Images |
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 12/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

![\left[ j_k,j_l \right] = i \sum_{m=1}ˆ3 \varepsilon_{klm}j_m \,](illustrations/6320282ba59ec95a06bf5f7dd517e1c7.png)
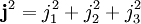
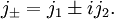
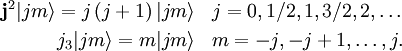
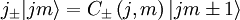
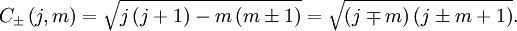
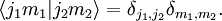
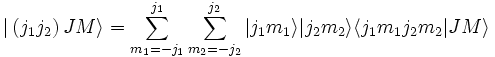
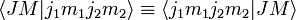
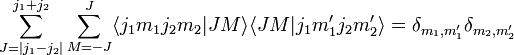
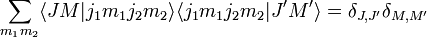
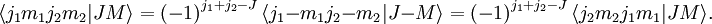
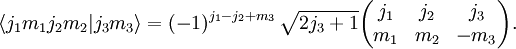

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité