Informatique quantique
L'informatique quantique est le sous-domaine de l'informatique qui traite des ordinateurs quantiques utilisant des phénomènes de la mécanique quantique, par opposition à ceux de l'électricité exclusivement, pour l'informatique dite «classique».
Recherche sur Google Images :

Source image : actumultimedia.unblog.fr Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- Plus sérieusement, l'informatique quantique est une idée, pour l'instant toujours.... en quantique, mais passons) peut être dans plusieurs états à la fois.... (source : developpez)
L'informatique quantique est le sous-domaine de l'informatique qui traite des ordinateurs quantiques utilisant des phénomènes de la mécanique quantique, par opposition à ceux de l'électricité exclusivement, pour l'informatique dite «classique». Les phénomènes quantiques utiles sont l'intrication quantique et la superposition. Les opérations ne sont plus basées sur la manipulation de bits, mais de qubits.
Selon la loi de Moore, la puissance des ordinateurs doit augmenter exponentiellement. Voyant cette «loi» envisageablement devenir fausse à court terme, une solution est de changer de paradigme pour se tourner vers l'informatique quantique.
Par contre, selon la thèse de Church, tout calcul devrait être faisable efficacement sur une machine de Turing, tandis qu'il ne semble pas envisageable de simuler un calculateur quantique avec une machine de Turing. Tout d'abord, un autre type d'ordinateur semblait avoir contredit cette thèse, le calculateur analogique. Cette contradiction apparente a néanmoins été rapidement réfutée parce que la question du bruit n'avait pas été abordée, et la surpuissance supposée du calculateur analogique est désormais nullifiée.
La prise en compte du bruit est par conséquent un des premiers défis du calculateur quantique. Surtout, la théorie de l'information quantique traite des codes correcteurs quantiques et du calcul quantique avec tolérance d'erreurs.
Résultats non négatifs
Deux résultats des années 1990 indiquent que les ordinateurs quantiques pourraient être plus puissants que les machines de Turing, et même des machines de Turing probabilistes. En 1994, Peter Shor découvre l'algorithme de Shor qui sert à calculer efficacement la décomposition en produit de facteurs premiers et le logarithme discret. En 1995, Lov Grover découvre l'algorithme de Grover qui sert à faire efficacement une recherche dans un espace non structuré.
Les problèmes résolus par l'algorithme de Shor n'ont pas de solution efficace connue sur un ordinateur classique, bref, sur une machine de Turing. Le perfectionnement en efficacité provenant de l'algorithme de Grover n'est pas aussi significative, mais la particulièrement grande applicabilité des algorithmes de recherche implique l'importance du résultat.
Les bases physiques
L'informatique quantique est basée sur la mécanique quantique. Les phénomènes utiles sont l'intrication quantique et la superposition. Il est cependant indispensable de prévoir les effets contre-productifs de la décohérence.
- Fonction d'onde
La fonction d'onde en mécanique quantique est la représentation de l'état quantique dans la base de dimension illimitée des positions. La probabilité de présence des particules représentées par cet état quantique est alors directement le carré de la norme de cette fonction d'onde.
- État quantique
En mécanique quantique, on représente l'état d'un dispositif par un point dans un espace vectoriel hilbertien ; l'espace à considérer dépendant du dispositif étudié. On utilise fréquemment la notation bra-ket pour représenter les états quantiques de manière simple. A titre d'exemple, l'espace des états d'une particule sans spin est l'espace des fonctions de 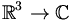 à carré sommable. Quand on associe deux dispositifs pour en faire un plus gros, l'espace des états de ce gros dispositif est le produit tensoriel des espaces des états associés aux deux sous-dispositifs.
à carré sommable. Quand on associe deux dispositifs pour en faire un plus gros, l'espace des états de ce gros dispositif est le produit tensoriel des espaces des états associés aux deux sous-dispositifs.
On retrouve aussi le déterminisme de la mécanique classique, c'est-à-dire qu'on peut calculer comment l'état d'un dispositif va évoluer au cours du temps (grâce à l'équation de Schrödinger), sauf quand il y a une mesure de l'état de notre dispositif, auquel cas l'évolution n'est plus déterministe, mais probabiliste.
Il s'agit là d'une différence majeure avec la mécanique classique, qui découle du postulat de réduction du paquet d'onde et qui sert à donner une interprétation probabiliste aux états quantiques.
Supposons qu'un dispositif quantique se trouve dans un état 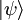 et qu'on veuille mesurer une observable
et qu'on veuille mesurer une observable 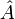 du dispositif (énergie, position, spin, ... ). Les vecteurs propres de
du dispositif (énergie, position, spin, ... ). Les vecteurs propres de 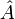 sont notés
sont notés 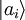 et les valeurs propres correspondantes αi, qu'on supposera non dégénérées pour simplifier. Comme le postule le principe de réduction du paquet d'onde, la mesure de A ne peut donner comme résultat que l'un des αi, et la probabilité d'obtenir le résultat αi est
et les valeurs propres correspondantes αi, qu'on supposera non dégénérées pour simplifier. Comme le postule le principe de réduction du paquet d'onde, la mesure de A ne peut donner comme résultat que l'un des αi, et la probabilité d'obtenir le résultat αi est 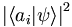 . Supposons que la mesure donne pour résultat αp, le dispositif est passé lors de la mesure et de façon instantanée de l'état
. Supposons que la mesure donne pour résultat αp, le dispositif est passé lors de la mesure et de façon instantanée de l'état 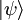 à l'état
à l'état 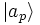 .
.
On voit par conséquent l'interprétation qu'on peut faire des produits scalaires 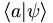 , où
, où 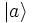 est un état quelconque : en effet, en supposant l'existence d'une observable dont
est un état quelconque : en effet, en supposant l'existence d'une observable dont 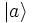 serait un des états propres, on peut dire que la probabilité de trouver le dispositif dans l'état
serait un des états propres, on peut dire que la probabilité de trouver le dispositif dans l'état 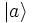 (sous-entendu : si on faisait la mesure) est
(sous-entendu : si on faisait la mesure) est 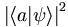 . Pour cette raison, le produit scalaire est nommé amplitude de probabilité.
. Pour cette raison, le produit scalaire est nommé amplitude de probabilité.
Il existe d'autres représentations mathématiques de l'état d'un dispositif, la matrice densité étant une généralisation de la représentation exposée ici.
Intrication quantique
En mécanique quantique, on nomme intricat un état physique où est intriqué un dispositif S1 & un dispositif S2 sans que l'espace de Hilbert soit la somme tensorielle de l'espace de S1 et de l'espace S2. Il y a même au contraire corrélation complète de S1 et de S2 de sorte que l'entropie de (S1 union S2) dans un intricat est simplement celle de S2 ou de S1. Il y a sous-additivité complète.
L'intrication quantique est la ressource naturelle principale, utilisée en informatique quantique : aujourd'hui, on la compare même au fer, tel que reconnu à l'Âge du bronze. De fait, la théorie de l'informatique quantique a énormément progressé depuis qu'on sait réaliser des intricats de faible décohérence : alors il est devenu pensable de prévoir un futur ordinateur quantique. Les mathématiciens (Shor, Kitæv, ... ) ont fondé le tout nouveau calcul quantique, qui est en train de révolutionner le calcul de la complexité algorithmique.
Bits vs qubits
Les opérations ne sont plus appliquées à des bits, mais à des qubits. L'espace des états envisageables n'est pas le même que dans le monde classique. Les deux qubits envisageables sont 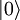 et
et 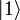 . Une différence majeure d'avec les bits, c'est qu'un qubit peut être dans les deux états en même temps : c'est le phénomène de superposition. Généralement, un qubit est
. Une différence majeure d'avec les bits, c'est qu'un qubit peut être dans les deux états en même temps : c'est le phénomène de superposition. Généralement, un qubit est
où | α | 2 + | β | 2 = 1. Donc, à la mesure, on trouve 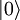 avec probabilité de α2 et
avec probabilité de α2 et 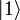 , avec une probabilité de β2. Surviennent ainsi les questions de mesure quantique, de distinction des états quantiques et de mesure projective.
, avec une probabilité de β2. Surviennent ainsi les questions de mesure quantique, de distinction des états quantiques et de mesure projective.
Il y a plusieurs façons physiques de représenter un qubit. Parmi celles-ci :
- spin d'électron
- niveaux d'énergie dans un atome
- polarisation d'un photon
Selon le principe de physique quantique, on conçoit le dispositif physique comme un espace de Hilbert à d dimensions. Pour traiter ceci, les outils mathématiques principaux se trouvent en algèbre linéaire. La notation habituelle pour les vecteurs est remplacée par la notation bra-ket telle qu'expliquée ci-haut pour les états quantiques ψ, puisque ce sont ces états qui sont représentés par des vecteurs.
Le vecteur aussi nommé ket :
Le vecteur dual (c'est à dire, transposé et conjugué) du ket, aussi nommé bra :
Les matrices typiquement utilisées sont : matrice hermitienne, matrice normale, matrice unitaire, matrice positive, matrice de densité, matrices de Pauli, matrice de Hadamard.
- Matrices de densité
Les matrices de densité sont des objets mathématiques qui peuvent traiter l'ensemble des types d'états quantiques utiles à l'informatique quantique : l'état pur tout comme l'état mélangé, qui est un mélange d'états purs.
- Opérations ou théorèmes utiles
Les matrices ont le plus souvent la fonction d'opérateurs linéaires. De plus, certaines opérations sur ces opérateurs sont aussi définies.
- Opérations sur les vecteurs
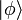 et
et 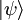 : produit scalaire
: produit scalaire 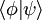 , produit tensoriel
, produit tensoriel 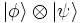 ou
ou 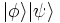
- Opérations sur les matrices A : conjugaison complexe A* ou hermitienne At, transposition AT, trace tr (A) , diagonalisation
- Mesures : mesure quantique, distinction des états quantiques et mesure projective. Les mesures projectives sont des opérateurs qui sont des projecteurs (Observables).
- Théorème de décomposition spectrale, inégalité de Cauchy-Schwarz
Algèbre abstraite
Du domaine de l'algèbre abstraite, les Groupes de Lie suivants sont utiles : SU (2) et SO (3) .
SU (2) , le groupe spécial unitaire de degré 2
Le groupe SU (2) est isomorphe au groupe des quaternions de valeur absolue 1 et est par conséquent semblable à la sphère de dimension 3 S3. Comme les quaternions représentent les rotations dans l'espace à 3 dimensions, il existe un homorphisme surjectif de groupes de Lie SU (2) → SO (3, R) de noyau {+I, –I}. Les matrices dites matrices de Pauli forment une base de su (2). Ces matrices sont fréquemment utilisées en mécanique quantique pour représenter le spin des particules.
SO (3) , le groupe orthogonal de degré 3 du corps 
Le groupe SO (3) , compris comme la totalité des rotations dans l'espace tridimensionnel, est nommé groupe des rotations.
En termes de topologie algébrique, pour n > 2, le groupe essentiel de SO (n) est le groupe cyclique d'ordre 2 et le groupe Spin Spin (n) est son recouvrement universel. Pour n=2, le groupe essentiel est le groupe cyclique illimité et son recouvrement universel correspond à la droite des réels.
- Pour l'article détaillé, voir complexité algorithmique quantique.
Une sous-branche de la complexité algorithmique pour traiter de l'algorithmique de l'informatique quantique.
Ordinateurs quantiques
- Pour l'article détaillé, voir calculateur quantique.
Un calculateur quantique opère ses calculs grâce, entre autre, à la superposition d'états quantiques. De petits calculateurs quantiques ont déjà été fabriqués dans les années 1990 et des progrès sont en cours. C'est un domaine en plein essor soutenu financièrement par de nombreuses organisations, entreprises ou gouvernements, du fait de l'importance de l'enjeu : révolutionner l'informatique avec une puissance et des opérations inimaginables avec un ordinateur classique.
La fabrication d'un ordinateur quantique nécessiterait l'utilisation de techniques qu'on commence à peine à maîtriser pour certaines.
Théorie de l'information quantique
- Pour l'article détaillé, voir théorie de l'information quantique.
Une sous-branche de la théorie de l'information pour traiter de l'information de l'informatique quantique. Les principaux sujets traités sont les codes correcteurs quantiques et le calcul quantique avec tolérance d'erreurs. La téléportation quantique joue aussi un rôle central.
Cryptographie quantique
- Pour l'article détaillé, voir cryptographie quantique.
La cryptographie quantique est une tentative de mise en œuvre des prédicats de la mécanique quantique afin d'assurer la confidentialité, l'intégrité ou la non-interception de transmissions de données.
La cryptographie quantique autorise deux interlocuteurs de s'échanger une clé en toute sécurité ; en effet, cette méthode permet non seulement de démasquer toute tentative d'espionnage grâce aux propriétés de la mécanique quantique, mais également de diminuer la quantité d'information détenue par un éventuel espion à un niveau arbitrairement bas et ce grâce à des algorithmes classiques. On le voit par conséquent, la cryptographie quantique forme un outil particulièrement précieux pour des dispositifs de cryptographie symétrique où les deux interlocuteurs doivent impérativement posséder la même clé et ce en toute confidentialité.
Voir aussi
|
Bibliographie
- (en) M. A. Nielsen et Isaac Chuang, Quantum Computation and Quantum Information, Cambridge University Press, 2000.
Liens externes
- (fr) Introduction à l'informatique quantique sans équations, Alexandre Blais (Yale)
- (en) Introduction à l'informatique quantique, pour les non-physiciens, Michel Le Bellac (CNRS)
- (en) Wiki d'informatique quantique
- (en) Quant-ph : articles de physique et d'informatique quantique
- (en) Quantum computation in Grenoble : Groupe de recherche en informatique quantique à Grenoble.
- Quantum Library : Bibliothèque C++ simulant le comportement de qubits donnant la possibilité le développement d'algorithme quantique
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

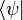


 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité