Théorie quantique des champs
La théorie quantique des champs est l'application des concepts de la physique quantique aux champs. Issue de la mécanique quantique relativiste, dont l'interprétation comme théorie décrivant une seule particule s'était avérée incohérente, cette...
Recherche sur Google Images :
Source image : map.gsfc.nasa.gov Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- ... de la théorie quantique des champs; est élaborée une nouvelle approche du ... des problèmes de mécanique quantique, de théorie quantique des champs et ... (source : msu)
- La théorie quantique des champs est fondée sur trois présupposés fondamentaux : la validité de la mécanique quantique, la validité du principe de relativité... (source : hourdequin.ifrance)
- La théorie quantique des champs est l'application de la mécanique quantique aux champs. Elle apporte un cadre beaucoup utilisé en physique des particules... (source : july.fixedreference)
La théorie quantique des champs (QFT, abréviation du terme anglais Quantum field theory) est l'application des concepts de la physique quantique aux champs. Issue de la mécanique quantique relativiste, dont l'interprétation comme théorie décrivant une seule particule s'était avérée incohérente, cette théorie apporte un cadre conceptuel beaucoup utilisé en physique des particules, en physique de la matière condensée et en physique statistique.
La première théorie quantique des champs à avoir vu le jour, l'électrodynamique quantique, est au XXIe siècle une des théories physiques ayant le plus beau succès dans sa confrontation aux résultats expérimentaux dans le cadre du modèle standard, surtout grâce à la concordance de la théorie avec la mesure de haute précision de la constante de structure fine.
Historique
La théorie naît en 1927 avec l'article fondateur de l'électrodynamique quantique par Dirac : La Théorie quantique de l'émission et de l'absorption du rayonnement. Le formalisme est ensuite développé et discuté dans les années 1930 par les théoriciens, ceux-ci se heurtant à un problème récurrent : la naissance systématique d'illimités lors des calculs de grandeurs physiques censées être mesurables et finies. Cette difficulté ne fut entièrement surmontée qu'en 1948 avec l'invention d'une procédure systématique, la renormalisation, due essentiellement à Tomonaga, à Schwinger ainsi qu'à Feynman.
Les succès de l'électrodynamique quantique, théorie de jauge abélienne, ont conduit les théoriciens des années 1960 et 1970 à appliquer les concepts de cette théorie aux théories de jauge non abéliennes, donnant finalement naissance à l'actuel modèle standard de la physique des particules.
D'autre part, Kadanoff a introduit à la fin des années 1960 l'idée que les transitions de phases décrites par la physique statistique présentaient des propriétés d'universalité et d'invariance d'échelles. Wilson eut alors l'idée d'appliquer les méthodes de renormalisation de la théorie quantique des champs à la description des phénomènes critiques.
La façon dont la théorie des champs fut introduite par Dirac à partir des particules élémentaires est réputée pour des raisons historiques sous l'appellation de seconde quantification.
- Les champs ne sont pas liés à la dualité onde-corpuscule.
Les particules élémentaires possèdent déjà cette dualité dans l'acceptation du terme de la mécanique classique. Ce qu'on entend par champ est un concept qui permet la création ou l'annihilation de particules en tout point de l'espace. Comme tout dispositif quantique, un champ quantique a un hamiltonien et obéit à l'équation de Schrödinger :
(En théorie des champs, le formalisme lagrangien est plus facile à utiliser que son équivalent hamiltonien. )
- Avec la seconde quantification, l'indiscernabilité des particules s'exprime en termes de nombre d'occupation.
Supposons que N = 3, avec une particule dans l'état φ1 et deux dans l'état φ2, alors la fonction d'onde est :
tandis qu'avec la seconde quantification, cette fonction est simplement
Quoique la différence soit minime, la seconde permet d'exprimer aisément des opérateurs création et annihilation, qui ajoutent ou enlèvent des particules à l'état. Ces opérateurs sont particulièrement identiques à ceux définis par un oscillateur harmonique quantique qui, en mécanique quantique, crée ou détruit des quanta d'énergie.
A titre d'exemple, l'opérateur a2 a l'effet suivant :
(Le facteur 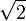 normalise la fonction d'onde. )
normalise la fonction d'onde. )
Enfin, il faut introduire «les opérateurs de champ» de création ou d'annihilation d'une particule en un point de l'espace.
De même que pour une seule particule la fonction d'onde s'exprime avec son moment cinétique, de même les opérateurs de champ peuvent s'exprimer avec transformées de Fourier.
A titre d'exemple, 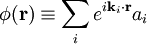 , qu'il ne faut pas confondre avec une fonction d'onde, est l'opérateur de champ d'annihilation de boson.
, qu'il ne faut pas confondre avec une fonction d'onde, est l'opérateur de champ d'annihilation de boson.
Les hamiltoniens, en physique des particules, sont rédigés comme une somme d'opérateurs création et annihilation de champ :
Cela exprime un champ de bosons libres, où Ek est l'énergie cinétique. Cet hamiltonien est utilisé pour décrire des phonons.
Localisation
L'expérimentateur qui enregistre un «clic» dans son détecteur aimerait relier cet événement, qu'il interprète comme la détection d'une «particule» assez bien située dans l'espace (et dans le temps), au champ quantique ainsi qu'à ses excitations, ce qui conduit au problème de la localisation[1] en physique quantique relativiste. Pour certains types de «particules», l'opérateur de position de Newton-Wigner apporte des éléments de réponse.
Notes
- ↑ Certains aspects de ce problème conceptuel sont discutés par Meinard Kuhlmann ; Quantum Field Theory, Stanford Encyclopedia of Philosophy (2006).
- Laverne, Alain ; Rayonnement quantique, cours donné en 1994 par Alain Laverne (Université Paris 7) sur la quantification du rayonnement électromagnétique et le concept de photon. 240 pages.
- Bell, John S. ; Théorie quantique des champs expérimentale, traduction française par Alain Laverne (Université Paris 7) d'un cours d'introduction donné en 1977 par John S. Bell (Physique Théorique, CERN) aux physiciens expérimentateurs. 41 pages.
- Delamotte, Bertrand ; Un soupçon de théorie des groupes : groupe des rotations & groupe de Poincaré, cours d'introduction pour physiciens (prolégomènes à un cours de théorie quantique des champs) donné en 1995 par Bertrand Delamotte (Laboratoire de Physique Théorique et Hautes Energies, Université Paris 7) au DEA "Champs, Particules, Matières". 127 pages.
- Laloë, Franck ; Cours sur les symétries, cours pour physiciens (prolégomènes à un cours de théorie quantique des champs) donné par Franck Laloë (Laboratoire de Physique Atomique, ENS Ulm, Paris) au DEA de Physique Quantique.
- Zinn-Justin, Jean ; Des illimités de la mécanique quantique relativiste au groupe de renormalisation, texte d'une conférence donnée par Jean Zinn-Justin (Service de Physique Théorique du CEA) lors de la 5e rencontre "Physique et Interrogations Principales" (PIF V) intitulée : L'élémentaire et le complexe. Universel et singulier (III) (27 octobre 1999, Collège de France, Paris). Publié par : Michel Crozon & Yves Sacquin (éditeurs), EDP Sciences (2001).
- Le Bellac, Michel ; Des phénomènes critiques aux champs de jauge - Une introduction aux méthodes ainsi qu'aux applications de la théorie quantique des champs, InterEditions/Editions du CNRS (1988), ISBN 2-86883-359-4. Réédité par EDP Sciences.
Textes en anglais
- Wilczek, Frank ; Quantum Field Theory, Review of Modern Physics 71 (1999) S85-S95. Article de revue rédigé par un Maître de la QCD, prix Nobel 2003. ArXiV : hep-th/9803075
- Zee, Anthony ; Quantum Field Theory in a Nutshell, Princeton University Press (2003), ISBN 0-691-01019-6. La meilleure introduction à la théorie quantique des champs. Pédagogique et même divertissant. Aspects de la théorie de la matière condensée comme de celle des hautes énergies.
- Ryder, Lewis H. ; Quantum Field Theory, Cambridge University Press (1985), ISBN 0-521-33859-X Ouvrage remarquable, qui complète à merveille le précédent pour la théorie quantique des champs appliquée à la physique des particules.
- Peskin, M and Schrœder, D. ;An Introduction to Quantum Field Theory (Westview Press, 1995), ISBN 0201503972. Pas à pas détaillé.
- Weinberg, Steven ; The Quantum Theory of Fields, Cambridge University Press (1995). Traité monumental en 3 volumes par un expert du domaine, prix Nobel 1979.
- Loudon, Rodney ; The Quantum Theory of Light (Oxford University Press, 1983), ISBN 0198511558
- Siegel, Warren ; Fields. ArXiV : arXiv :hep-th/9912205). Atypique.
- 't Hooft, Gerard ; The Conceptual Basis of Quantum Field Theory, Handbook of the Philosophy of Science, Elsevier (à paraître). Article de revue rédigé par un Maître des théories de jauge, prix Nobel 1999. pdf.
- Srednicki, Mark ; Quantum Field Theory
- Maggiore, Michele ; A Modern Introduction to Quantum Field Theory, Oxford University Press (2005), ISBN 0-19-852074-3.
Une introduction à la théorie quantique des champs qui présente les méthodes modernes de la physique théorique. Basé sur son cours de quatrième année à l'Université de Genève, ce livre s'adresse à des étudiants n'ayant aucune connaissances préalables en principe quantique des champs.
Voir aussi
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

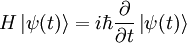
![\frac{1}{\sqrt{3}} \left[
\phi_1(r_1) \phi_2(r_2) \phi_2(r_3) +
\phi_2(r_1) \phi_1(r_2) \phi_2(r_3) +
\phi_2(r_1) \phi_2(r_2) \phi_1(r_3) \right]](illustrations/833350313ed2b1360d056ca0cb7d768c.png)
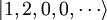
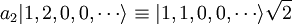
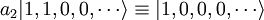
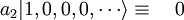
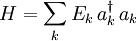

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité