Théorème adiabatique
Le théorème adiabatique est un concept important en mécanique quantique. Sa forme originelle, énoncée en 1928 par Max Born et Vladimir Fock, peut être énoncée de la manière suivante ...
Le théorème adiabatique est un concept important en mécanique quantique. Sa forme originelle[1], énoncée en 1928 par Max Born et Vladimir Fock, peut être énoncée de la manière suivante :
- Un dispositif physique est tenu dans son état propre instantané si une perturbation donnée agit sur lui suffisamment lentement et si il y a un intervalle significatif entre la valeur propre et le reste du spectre du hamiltonien.
Il peut ne pas être immédiatement compris à partir de cette formulation que le théorème adiabatique est , en fait, un concept extrêmement intuitif. Formulé simplement, un dispositif quantique soumis à des conditions externes de modification graduelle peut adapter sa forme fonctionnelle, tandis que dans le cas de modifications rapides, l'adaptation n'a pas le temps de se produire et donc la densité de probabilité reste inchangée.
Les conséquences de ce résultat simple en apparence sont nombreuses, variées et extrêmement subtiles. Pour clarifier ce propos, on débutera cet article par un description qualitative, suivie par quelques exemples avant d'entamer une analyse rigoureuse. Enfin, on présentera quelques techniques utilisées pour les calculs d'adiabaticité.
Un processus diabatique est un processus dans lequel les conditions (externes) changeant rapidement empêchent le dispositif d'adapter sa configuration durant son déroulement, ce qui fait que la densité de probabilité reste inchangée. Typiquement, il n'y a pas d'état propre du hamiltonien final de même forme fonctionnelle que pour l'état d'origine. Le dispositif finit en une combinaison linéaire d'états dont la somme reproduit la densité de probabilité d'origine.
Un processus adiabatique est un processus dans lequel les conditions (externes) permette l'adaptation du dispositif, donnant la possibilité la modification de la densité de probabilité. Si le dispositif est originellement dans un état propre du hamiltonien de départ, il sera au final dans l'état propre «correspondant» du hamiltonien d'arrivée[2].
Différentiation théorique
Pour un temps d'origine un dispositif quantique a une énergie donnée par le hamiltonien ; le dispositif est dans un état propre de décrit par. Les conditions changeantes modifient le hamiltonien de manière continue, ce qui donne un hamiltonien final à un temps. Le dispositif évolue selon l'équation de Schrödinger, afin d'atteindre l'état final. Le théorème adiabatique indique que la modification du dispositif dépend de manière critique du temps durant lequel elle a lieu.
Pour un processus adiabatique véritable, on utilise ; dans ce cas, l'état final est un état propre du hamiltonien final, avec une configuration modifiée :
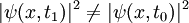 .
.
Le degré auquel un changement donné approche un processus adiabatique dépend à la fois de la séparation énergétique entre et les états adjacents, et la rapport entre l'intervalle à l'échelle de temps caractéristique de l'évolution de pour un hamiltonien indépendant du temps,, où est l'énergie de.
Inversement, dans la limite on a un passage illimitément rapide, ou diabatique ; la configuration de l'état reste inchangé :
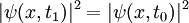 .
.
La condition dite «de gap» incluse dans la définition originale de Born et Fock donnée plus haut se réfère à la condition que le spectre de soit discret et non dégénéré, c'est-à-dire qu'il n'existe pas d'ambigüité dans l'ordre des états (on peut aisément établir quel état propre de correspond à). En 1990, J. E. Avron et A. Elgart reformulèrent le théorème adiabatique, éliminant la condition de gap[3].
Le terme adiabatique est habituellement utilisé en thermodynamique pour décrire des processus sans échange de chaleur entre le dispositif et son environnement (voir adiabaticité). La définition quantique est plus proche du concept thermodynamique de transformation quasi-statique, et n'a pas de relation directe avec l'échange de chaleur. Ces deux définitions différentes peuvent être sources de confusion, en particulier quand les deux concepts (échange de chaleur et processus suffisamment lents) sont présents dans un problème spécifique.
On considère généralement l'exemple du pendule oscillant dans un plan vertical. Si le support est déplacé, le mode d'oscillation du pendule change. Si le support est déplacé suffisamment lentement, le mouvement du pendule relatif au support reste inchangé. Un changement graduel dans les conditions externes permet au dispositif de s'adapter, tel que le caractère d'origine soit conservé. Cela est un processus adiabatique au sens quantique du terme[4].
Oscillateur harmonique quantique
La nature classique d'un pendule exclut une description complète des effets du théorème adiabatique. Comme exemple, on considèrera un oscillateur harmonique quantique quand la constante de rappel augmente. C'est l'équivalent classique de la raideur d'un ressort ; quantiquement, l'effet est un rétrécissement de la courbe d'énergie potentielle dans le hamiltonien du dispositif.
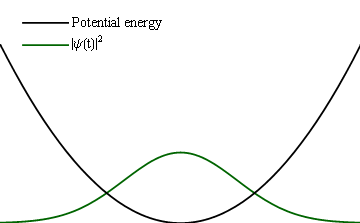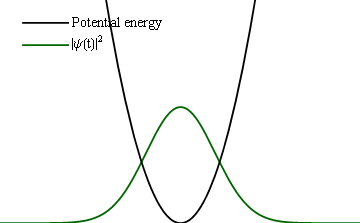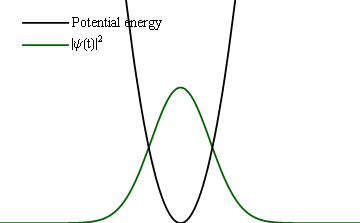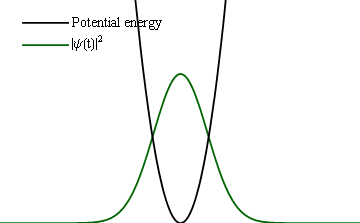
Si est accru adiabatiquement, alors le dispositif au temps sera dans un état propre instantané du hamiltonien courant, correspondant à l'état propre d'origine de. Pour le cas spécial d'un dispositif, comme l'oscillateur quantique harmonique, décrit par un seul nombre quantique, cela veut dire que le nombre quantique restera inchangé. La figure 1 montre comment un oscillateur harmonique, originellement dans son état essentiel,, reste dans cet état essentiel lorsque la courbe d'énergie potentielle est compressée ; la forme fonctionnelle de l'état s'adaptant aux conditions variant lentement.
Pour une constante de rappel croissant rapidement, le dispositif subit un processus diabatique dans lequel le dispositif n'a pas le temps d'adapter sa forme fonctionnelle aux conditions changeantes. Tandis que l'état final doit être semblable à l'état d'origine pour un processus opérant sur une période de temps non prise en compte, il n'y a pas d'état propre du nouveau hamiltonien,, qui est comparable à l'état d'origine. En fait l'état d'origine se compose d'une superposition linéaire de nombreux états propres différents de dont la somme reproduit la forme de l'état d'origine.
Croisement de courbe évité
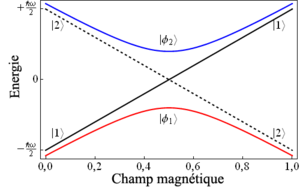
Pour un exemple plus largementappliqué, considérons un atome à deux niveaux soumis à un champ magnétique externe[5]. Les états désignés par et dans la notation bra-ket, peuvent être conçus comme des états de moment angulaire atomique, chacun possédant une géométrie spécifique. Pour des raisons qui seront éclaircies ensuite, ces états seront nommés états diabatiques dans la suite de cet article. La fonction d'onde du dispositif peut être représentée comme une combinaison linéaire des états diabatiques :
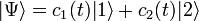 .
.
En l'absence de champ, la séparation énergétique des états diabatiques est identique à ; l'énergie de l'état croît avec l'augmentation du champ magnétique (état de champ faible), tandis que l'énergie de l'état décroît dans le même temps (état de champ fort). Si on suppose la dépendance au champ magnétique linéaire, la matrice hamiltonienne du dispositif peut s'écrire :
où est le moment magnétique de l'atome, qu'on considère être le même pour les deux états diabatiques, et est un couplage entre les deux états. Les éléments diagonaux sont les énergies des états diabatiques (et). Cependant, comme n'est pas une matrice diagonale, il est clair que ces états ne sont pas états propres du hamiltonien.
Les vecteurs propres de la matrice sont les états propres du dispositif, qu'on désignera par et, avec les valeurs propres correspondantes :
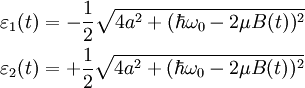 .
.
Il est important de réaliser que les valeurs propres sont les seuls états du dispositif permis ; une mesure de l'énergie du dispositif au temps donnera soit, soit. Les états diabatiques et sont des combinaisons linéaire des états propres alors que les énergies diabatiques du dispositif et correspondent aux espérances mathématiques pour l'énergie du dispositif dans les états diabatiques et respectivement.
La figure 2 montre la dépendance des énergies diabatiques et adiabatiques selon la valeur du champ magnétique ; notons que pour un couplage non-nul les valeurs propres du hamiltonien ne peuvent être dégénérés, et par conséquent nous sommes en présence d'un croisement évité. Si un atome est originellement dans un état dans un champ magnétique nul (courbe rouge, à l'extrême gauche), une augmentation adiabatique du champ magnétique impose au dispositif de rester dans un état propre du hamiltonien (en suivant la courbe rouge, par conséquent). Un accroissement diabatique du champ magnétique impose au dispositif de suivre le chemin diabatique (ligne noire continue), par conséquent une transition vers l'état. Pour des variations finies du champ magnétique, il existe une probabilité finie de trouver un dispositif dans un des deux états propres. On pourra se reporter ci-dessous pour le calcul de ces probabilités.
Ces calculs sont particulièrement importants en physique atomique et moléculaire pour le contrôle de la distribution des états d'énergie dans une population d'atomes ou de molécules.
Conditions induites pour le passage entre diabaticité et adiabaticité
Continuons désormais avec une analyse plus rigoureuse[6]. En utilisant la notation bra-ket, le vecteur d'état du dispositif au temps peut être rédigé :
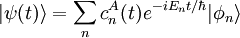 ,
,
où la fonction d'onde spatiale déjà mentionnée jusque là, est la projection du vecteur d'état sur les états propres de l'opérateur position
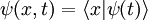 .
.
Il est intéressant de considérer les cas limites, dans lesquels est soit particulièrement grand (adiabatique, ou modification graduelle) ou soit particulièrement petit (diabatique, ou modification soudaine). Soit un hamiltonien du dispositif subissant une modification continue depuis un état d'origine, au temps, jusqu'à un état final, au temps math>\scriptstyle{t_1}, où. L'évolution du dispositif peut être décrit dans la représentation de Schrödinger par un opérateur temporel, défini par l'équation intégrale :
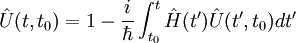 ,
,
équivalent à l'équation de Schrödinger :
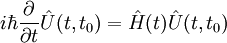 ,
,
avec pour condition d'origine. Connaissant la fonction d'onde du dispositif à, l'évolution du dispositif jusqu'à un temps ultérieur peut être obtenue par :
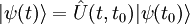 .
.
Le problème de la détermination de l'adiabaticité d'un processus donné est équivalent à établir la dépendance de à.
Pour déterminer la validité de l'approximation adiabatique d'un procédé donné, on peut calculer la probabilité de trouver le dispositif dans un état autre que celui dans lequel il a débuté. En utilisant la notation bra-ket et la définition, on a :
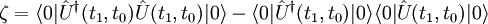 .
.
On peut développer :
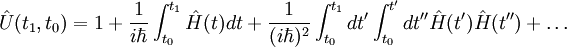 .
.
Dans la limite de perturbation, on peut prendre en compte les seuls deux premiers termes et les substituer dans l'équation pour, en notant que :
est le hamiltonien du dispositif, moyenné sur l'intervalle, d'où :
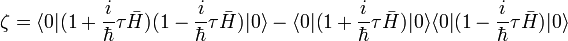 .
.
Après avoir développé les produits et procédé aux éliminations appropriées, on a :
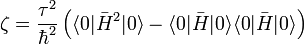 ,
,
ce qui donne :
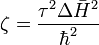 ,
,
où est la valeur efficace du hamiltonien du dispositif moyenné sur tout l'intervalle étudié.
L'approximation soudaine est valide lorsque (la probabilité de trouver le dispositif dans un état autre que celui d'origine est proche de 0), ce qui fait que la condition de validité est donnée par :
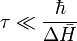 ,
,
ce qui est , en fait, un énoncé du principe d'incertitude de Heisenberg dans sa forme liant temps et énergie.
Passage diabatique
A la limite, on a un passage illimitément rapide, ou diabatique :
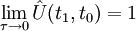 .
.
La forme fonctionnelle du dispositif reste inchangée :
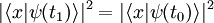 .
.
On l'appelle quelquefois approximation soudaine. La validité de l'approximation pour un processus donné peut être déterminée à partir de la probabilité que l'état du dispositif reste inchangé :
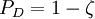 .
.
Passage adiabatique
A la limite, on a un passage illimitément lent, ou adiabatique. Le dispositif évolue, adaptant sa forme aux conditions changeantes :
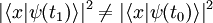 .
.
Si le dispositif est originellement dans un état propre de, après un temps il sera passé dans l'état propre correspondant de. On l'appelle l'approximation adiabatique. La validité de l'approximation pour un processus donné peut être déterminée à partir de la probabilité pour que l'état final du dispositif soit différent de l'état initial :
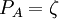 .
.
En 1932, une solution analytique au problème du calcul des probabilités de transition diabatique fut publié scindément par Lev Landau et Clarence Zener[7], pour le cas spécifique de la perturbation changeant linéairement dans laquelle la composante dépendant du temps n'est pas couplée aux états pertinents (donc le couplage dans la matrice hamiltonienne diabatique est indépendant du temps).
Le principal apport de cette approche est la vélocité de Landau-Zener :
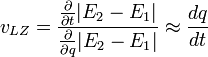 ,
,
où est la variable de pertubation (champ magnétique ou électrique, longueur de liaison moléculaire, ou toute autre perturbation du dispositif), et et sont les énergies des deux états diabatiques (se croisant). Une grande implique une grande probabilité de transition diabatique et vice versa.
Si on utilise la formule de Landau-Zener, la probabilité d'une transition diabatique est donnée par :
Approche numérique
Pour une transition impliquant une modification non-linéaire de la variable de perturbation ou du couplage dépendant du temps entre les états diabatiques, les équations cinétiques de la dynamique du dispositif ne sont pas analytiquement solvables. La probabilité de transition diabatique peut toujours être obtenue en utilisant une grande variété de algorithmes de résolution numérique des équations différentielles ordinaires.
Les équations à résoudre peuvent être obtenues à partir de l'équation de Schrödinger dépendante du temps :
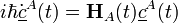 ,
,
où est un vecteur contenant les amplitudes de l'état adiabatique, est le hamiltonien adiabatique dépendant du temps[5] et le point supérieur indique une dérivée temporelle.
Une comparaison des conditions initiales utilisées avec les valeurs des amplitudes de l'état selon la transition peut indiquer la probabilité de transition diabatique. On a surtout, pour un dispositif à deux états :
si le dispositif est initialisé avec.
Voir aussi
- Formule de Landau-Zener
- Phase de Berry
- Approximation de Born-Oppenheimer
Références
- ↑ M. Born et V. A. Fock, «Beweis des Adiabatensatzes», dans Zeitschrift für Physik A Hadrons and Nuclei, vol. 51, no 3-4, 1928, p. 165-180 [texte intégral]
- ↑ T. Kato, «On the Adiabatic Theorem of Quantum Mechanics», dans Journal of the Physical Society of Japan, vol. 5, no 6, 1950, p. 435-439 [texte intégral]
- ↑ J. E. Avron et A. Elgart, «Adiabatic Theorem without a Gap Condition», dans Communications in Mathematical Physics, vol. 203, no 2, 1999, p. 445-463 [texte intégral lien DOI]
- ↑ David J. Griffiths, Introduction to Quantum Mechanics, Pearson Prentice Hall, 2005 (ISBN 0-13-111892-7) , chap. X
- ↑ a b S. Stenholm, «Quantum Dynamics of Simple Systems», dans The 44th Scottish Universities Summer School in Physics, 1994, p. 267–313
- ↑ Messiah, Albert (1999). "XVII", Quantum Mechanics. Dover Publications, Inc.. ISBN 0-486-40924-4.
- ↑ C. Zener, «Non-adiabatic Crossing of Energy Levels», dans Proceedings of the Royal Society of London, Series A, vol. 137, no 6, 1932, p. 692–702 [texte intégral lien DOI]
- (en) Cet article est partiellement ou en totalité issu d'une traduction de l'article de Wikipédia en anglais intitulé «Adiabatic theorem».
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

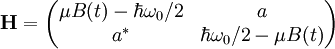
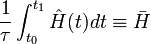
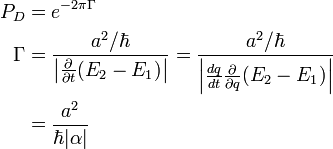
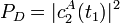

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité