Particule dans une boîte
En physique, la particule dans une boîte est une représentation simple d'un dispositif relevant de la mécanique quantique.
Recherche sur Google Images :

Source image : fr.wikipedia.org Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- La particule dans la boite. Considerons l'équation d'une particule dans une boite de largeur l. L'éation de Schrodinger s'érit :... (source : ensmp)
- Particule dans une boite cylindrique. I. 1 équations générales. I. 1.1 équation de Schrödinger générale. Dans le cadre de la mécanique quantique une particule... (source : crayonsuivant)
- ... de l'équation de Schrodinger pour une particule dans une boite avec potentiel... Les équations de Maxwell sous forme intégrale et différentielle sont ... (source : rmc)
En physique, la particule dans une boîte (ou puits de potentiel carré) est une représentation simple d'un dispositif relevant de la mécanique quantique. On étudie une particule confinée dans une région finie de l'espace grâce à des murs de potentiel illimité aux bords de cette région. La particule n'est soumise à aucune force au sein de la boîte, mais y est retenue par une force illimitée aux bords. C'est une situation comparable à un gaz confiné dans un contenant. Pour simplifier, le cas unidimensionel sera premièrement traité. On en déduira les équations des cas bi- et tridimensionnel.
La solution de l'équation de Schrödinger pour une particule dans le problème d'une boîte révèle des comportements quantiques qui sont en accord avec l'expérience, mais contraires aux prédictions de la mécanique classique. C'est une illustration utile puisque ce comportement n'est pas «forcé» par le dispositif, il provient naturellement des conditions initiales.
Le comportement quantique d'une particule libre dans une boîte consiste en :
- La quantification de l'énergie - La particule ne peut prendre que certaines valeurs d'énergie bien définies (discrétisation de l'énergie). Le résultat d'un tel dispositif en mécanique classique démontrerait que le dispositif peut prendre l'ensemble des valeurs d'énergie envisageables (valeurs continues, ou continuum).
- Un État essentiel - L'énergie la plus basse est strictement supérieure à zéro.
- Nœuds - À l'inverse de la mécanique classique, l'équation de Schrödinger prédit que certains états possèdent des nœuds, donnant lieu à des positions où la particule ne peut pas être trouvée.
Réalisation
La réalisation est fréquemment effectuée avec la croissance de cristaux sur un substat semiconducteur (Silicium, GaAs... ). On obtient ainsi une sorte d'atome artificiel, énormément plus grand en fait (∼100x), mais dont on peut à loisir choisir les raies d'absorption (couleur et propriétés physiques). Une de ces boîtes quantiques est utilisée industriellement dans un émetteur à fréquence variable dont un effort sur le cristal entraîne une modification de la fréquence.
Le cas de la particule dans une boîte unidimensionnelle
Pour le cas unidimensionel, par exemple dans la direction de l'axe x, l'équation de Schrödinger indépendante du temps peut-être rédigée comme :
où
où h est la constante de Planck, m est la masse de la particule, ψ est la fonction d'onde (pouvant être complexe) que nous devons trouver, V (x) est une fonction décrivant le potentiel pour chaque valeur de x et E est l'énergie, un nombre réel. Pour le cas de la particule dans une boîte unidimensionelle de longueur L, le potentiel est zéro au sein de la boîte, et vaut l'infini en x = 0 et x = L. Pour la région au sein de la boîte V (x) = 0 et l'équation 1 se réduit à :
Il s'agit là d'un problème bien connu de valeurs propres dont la solution générale est
où A et B sont des nombres complexes, et k est un nombre réel (k doit être réel parce que E est réel).
Maintenant, pour trouver les solutions spécifiques pour le problème d'une particule dans un puits de potentiel, nous devons spécifier les conditions aux limites et trouver les valeurs de A et de B qui satisfont ces conditions. Premièrement, on impose ψ identique zéro pour x = 0 et x = L. Ces conditions peuvent être interprétées comme une valeur illimitée du potentiel en ces positions, par conséquent il est impossible de retrouver la particule à ces lieux. Ainsi, la probabilité de retrouver la particule, soit |ψ|2, doit être petite dans ces régions et diminue quand le potentiel augmente. Dans le cas d'un potentiel illimité, |ψ|2 doit être nulle, d'où ψ doit être nulle dans cette région. En résumé,
Deuxièmement, on trouvera les solutions correspondant à la section de propagation libre à la fin de cet article : ce cas de figure ne contraint pas la fonction d'onde à s'annuler aux limites. Cela veut dire que lorsque la particule atteint une frontière du puits, elle disparaît instantanément de ce côté du puits pour réapparaître de l'autre coté, comme si le puits était une sorte de tore. La valeur des solutions est discutée dans la partie appropriée. Nous reprenons désormais la dérivation avec des conditions d'annulation à la frontière.
En remplaçant la solution générale de l'équation 3 dans l'équation 2 et en se plaçant en x = 0 (ψ = 0), nous trouvons que B = 0 (car sin (0) = 0 and cos (0) = 1). Il s'ensuit que la fonction d'onde doit être de la forme :
et en x = L nous trouvons :
Une solution pour l'équation 6 est A = 0, cependant, cette «solution triviale» impliquerait que ψ = 0 en tout point (i. e. la particule n'est pas dans la boîte) et peut être mise à l'écart. Si A ≠ 0 alors sin (kL) = 0, ce qui est uniquement vrai quand :
(remarquez que n = 0 ne convient pas car alors ψ=0 en tout point, correspondant au cas où la particule n'est pas dans la boîte). Les valeurs négatives de n sont aussi négligées, car elles changent simplement le signe de sin (nx). Désormais pour trouver A, on utilise le fait que la probabilité de trouver la particule quelque part est identique à 1. D'où la valeur de l'intégrale de |ψ|2 sur l'axe x :
or
Ainsi, A peut être tout nombre complexe de norme √ (2/L) ; ces différentes valeurs de A correspondent au même état physique. On choisit par conséquent A = √ (2/L) pour simplifier.
Finalement, en remplaçant les résultats de l'équation 7 et 8 dans l'équation 3 on obtient la solution complète pour le problème d'une particule unidimensionnelle dans une boîte :
Remarquons que, comme mentionné auparavant, seuls des niveaux d'énergie «quantifiés» sont envisageables. Aussi, puisque n ne peut être nul, la plus basse énergie selon l'équation 9, est aussi non nulle. Cet état essentiel d'énergie non nulle peut être expliqué par le principe d'incertitude. Puisque la particule est astreinte à se déplacer dans une région finie, la variance dans ses positions est majorée. Ainsi selon le principe d'incertitude la variance de l'impulsion (quantité de mouvement) de la particule ne peut être nulle, la particule possède par conséquent une certaine quantité d'énergie qui augmente lorsque que la longueur de la boîte, L, diminue.
Aussi, puisque ψ se compose d'ondes sinusoïdales, pour quelques valeurs de n supérieures à un, il y a des régions dans la boîte pour lesquels ψ et mais aussi ψ2 sont identiques à 0, indiquant mais aussi pour ces niveaux d'énergie, des nœuds existent dans la boîte où la probabilité de trouver une particule est nulle.
La particule dans une boîte à 2 ou 3 dimensions
Pour le cas bidimensionnel, la particule est confinée dans une surface rectangulaire de longueur Lx dans la direction x et Lydans la direction y. Le potentiel est toujours nul dans la «boîte» et illimitée sur les murs. Pour la zone intérieure de la boîte, où le potentiel est nul, l'expression bidimensionnelle analogue à l'équation 2 s'écrit :
Dans ce cas ψ est une fonction de x et d'y, d'où ψ=ψ (x, y). Pour résoudre l'équation 11, on utilise une méthode de séparation des variables. Initialement, nous supposons que ψ peut s'exprimer comme un produit de deux fonctions indépendantes, la première dépendant uniquement de x et la seconde uniquement de y, i. e. :
En remplaçant l'équation 12 dans l'équation 11 et en évaluant les dérivées partielles :
ce qui lors de la division par XY et en posant d2X/dx2 = X"et d2Y/dy2= Y" devient :
On remarque à présent que puisque X"/X est indépendant de y, une variation de y peut uniquement changer le terme Y"/Y. Cependant, selon l'équation 14, faire fluctuer Y"/Y sans faire fluctuer X"/X, change aussi E, or E est constant, par conséquent Y"/Y doit aussi être une constante indépendante de Y. Le même raisonnement est parfois utilisé pour montrer que X"/X est indépendant de x. Puisque X"/X et Y"/Y sont constants, on peut écrire :
où Ex + Ey = E. En utilisant la notation précédente pour X" et Y" on obtient :
chacune de ces équation est de la même forme que l'équation de Schrödinger unidimensionnelle (équation 2) que nous avons résolue dans la section précédente. Ainsi, selon la partie précédente nous avons :
Finalement, puisque ψ=XY et E = Ex + Ey, on obtient les solutions :
La même technique de séparation de variables peut être appliquée au cas tri-dimensionnel pour donner la solution :
Une propriété intéressante des solutions ci-dessus est que lorsque deux ou plus des longueurs sont les mêmes (eg. Lx = Ly), il y a plusieurs fonctions d'onde correspondant à la même énergie totale. Par exemple la fonction d'onde avec nx = 2, ny = 1 a la même énergie que la fonction d'onde avec nx = 1, ny = 2. Cette situation est nommée dégénérescence. Pour le cas où précisément deux fonctions d'onde dégénérées ont la même énérgie, ce niveau d'énergie est dit doublement dégénéré. La dégénérescence résulte de la symétrie du dispositif. Pour le cas ci-dessus, deux des longueurs sont identiques, le dispositif est par conséquent symétrique avec une rotation de 90°.
Propagation libre
Si le potentiel est nul (ou constant) en tout point, on définit une particule libre. Ceci apporte quelques difficultés de normalisation de la fonction d'onde. Une manière de contourner le problème est de contraindre la particule dans un volume fini V de grandeur arbitraire, dans lequel il n'y a pas d'obstacle à la propagation. Il faut que quand V→ ∞, on récupère la particule libre, tout en donnant la possibilité dans les calculs intermédiaires l'utilisation des états correctement normalisés. Aussi, lorsque nous décrivons par exemple une particule se déplacant dans un solide, on ne s'attend pas à des états situés spatialement mais au contraire à des états totalement délocalisés (dans le solide), ce qui veut dire que la particule se propage à travers lui (dans la mesure où elle peut être partout avec la même probabilité, à l'inverse des solutions sinusoïdales que nous avons rencontrées quand la particule a des localisations préférentielles). Cette interprétation découle des solutions de l'équation de Schrödinger pour un potentiel nul avec les conditions aux limites dites "Von-Karman boundary conditions ", i. e. la fonction d'onde prend les mêmes valeurs sur les faces opposées de la boîte, mais pas obligatoirement nulles. On vérifie ensuite que les fonctions suivantes sont solution de l'équation 1 :
L'énergie reste 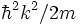 (cf. eq. 3) mais ici les k ont des valeurs doubles de ceux de la solution précédente (cf. eq. 7). C'est parce que, dans le cas précédent, n était strictement positif tandis qu'ici il peut être négatif ou nul (l'état essentiel). Les solutions où la fonction sinusoïdale ne se superpose pas sur elle-même après une translation de L ne peuvent pas être trouvés avec une exponentielle, puisque dans cette interprétation d'une particule qui se propage, la dérivée est discontinue aux bords, cela veut dire que la particule prend une vitesse illimitée à cet lieu. Cela montre que les deux interprétations traduisent des comportements intrinsèquement différents.
(cf. eq. 3) mais ici les k ont des valeurs doubles de ceux de la solution précédente (cf. eq. 7). C'est parce que, dans le cas précédent, n était strictement positif tandis qu'ici il peut être négatif ou nul (l'état essentiel). Les solutions où la fonction sinusoïdale ne se superpose pas sur elle-même après une translation de L ne peuvent pas être trouvés avec une exponentielle, puisque dans cette interprétation d'une particule qui se propage, la dérivée est discontinue aux bords, cela veut dire que la particule prend une vitesse illimitée à cet lieu. Cela montre que les deux interprétations traduisent des comportements intrinsèquement différents.
//A terminer//
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

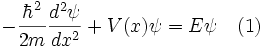
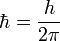

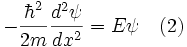
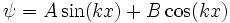
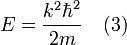
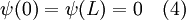
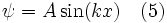
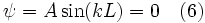
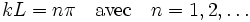
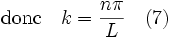
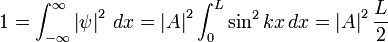
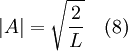
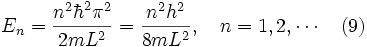
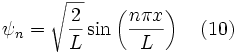
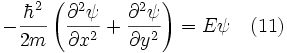
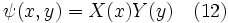
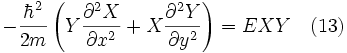
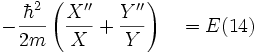
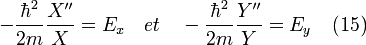
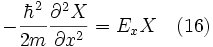
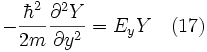
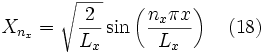
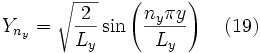
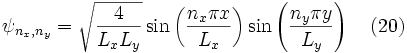
![E_{n_x,n_y} = \frac{hˆ2}{8m} \left[ \left( \frac{n_x}{L_x} \right)ˆ2 + \left( \frac{n_y}{L_y} \right)ˆ2 \right] \quad (21)](illustrations/c31191811c2882201107f6d908116daf.png)
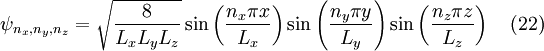
![E_{n_x,n_y,n_z} = \frac{hˆ2}{8m} \left[ \left( \frac{n_x}{L_x} \right)ˆ2 + \left( \frac{n_y}{L_y} \right)ˆ2 + \left( \frac{n_z}{L_z} \right)ˆ2 \right] \quad (23)](illustrations/30305475bcdeb54b54214faaaff08d32.png)
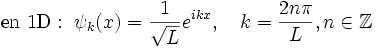
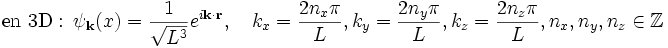

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité