Spectre d'ondes planes
La décomposition d'une onde de forme quelconque sur une base d'ondes planes est une opération usuelle dans différents domaines de la physique, par exemple en optique ou en mécanique quantique.
Recherche sur Google Images :
Source image : www.d-faz.ca Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- numérique à une antenne de station de base. Après obtention du spectre d'ondes planes à partir des données du champ électrique tangentiel prélevé sur un... (source : books.google)
- sur une décomposition en ondes planes monochromatiques du champ ultrasonore.... peut s'exprimer comme la somme d'ondes planes monochromatiques... L'expression (2) donne le spectre spatio-temporel du faisceau dans le plan de référence, ... (source : hal.archives-ouvertes)
- Dans le cas où les deux ondes ont la même pulsation, le champ électrique est : E (r, t) = 2E.... d'ondes planes progressives monochromatiques... Spectre d'une onde et enveloppe temporelle. Pour vous familiari- ser avec la transfor-... (source : edu.upmc)
Introduction
La décomposition d'une onde de forme quelconque sur une base d'ondes planes est une opération usuelle dans différents domaines de la physique, par exemple en optique ou en mécanique quantique.
Dans certaines géométries de sources, il est fait appel au principe de Huygens pour obtenir le champ à longue, ou particulièrement longue distance : une surface d'onde donnée est reconnue comme sources d'ondes sphériques dont la combinaison apportera le champ à l'endroit voulu.
La méthode du spectre d'ondes planes procède d'une tout autre manière, sans nécessiter d'appel à un principe supplémentaire. Elle apparaît singulièrement efficace si le champ source, à propager, est connu dans un plan.
Une simple transformée de Fourier bidimensionnelle mène à l'obtention d'une expression analytique valable en tout point de l'espace tridimensionnel. On retrouve ainsi en quelques lignes de calcul les approximations usuelles de Fresnel, ou de Fraunhoffer, mais en plus, l'expression obtenue est bonne pour le champ proche, ce que ne donne pas l'approche utilisant le principe de Huygens.
La méthode peut être appliquée dans de nombreux cas, où la source est effectivement plane. Par exemple dans le cas d'une fente source dans un écran plat ; en première approximation le champ incident sur l'écran est découpé à l'emporte pièce, ce qui est habituellement fait. En dehors de cette difficulté, qui a son importance, le calcul est valide, pour chaque composante du champ vectoriel, s'il y a lieu, et , ce, à toute distance.
Aperçu mathématique
Soit f un champ scalaire monochromatique de pulsation 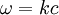 , satisfaisant à une équation de Helmholtz (une adaptation peut-être réalisée pour l'équation de Schrödinger, ou autres équations de propagation, ou de diffusion) :
, satisfaisant à une équation de Helmholtz (une adaptation peut-être réalisée pour l'équation de Schrödinger, ou autres équations de propagation, ou de diffusion) :
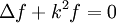 .
.
Une onde plane est une solution spécifique cette équation. Une solution générale peut être rédigée par linéarité de l'équation de Helmholtz comme une superposition d'ondes planes se propageant dans l'ensemble des directions envisageables dans le demi-espace z > 0.
Par hypothèse le champ f (x, y, z) est connu dans le plan z = 0, plan sur lequel on évalue la transformée de Fourier :
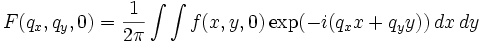 .
.
La transformée de Fourier du champ dans un plan localisé à une cote z est alors tout simplement :
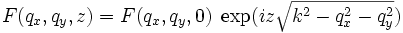 .
.
Ainsi obtient-on, dans le plan z quelconque, le champ f (x, y, z) par une simple transformation de Fourier inverse :
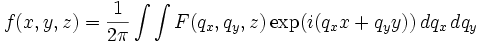 ,
,
qui est la solution exacte.
Dans cette expression, les hautes fréquences spatiales (méthode de la phase stationnaire. Cette approximation mène pour de longues distances aux formules de Fresnel (facteur d'obliquité inclus) ainsi qu'à celles de Fraunhoffer pour de particulièrement longue distance.
A titre d'exemple, dans le cas de l'approximation de Fraunhoffer, on trouve :
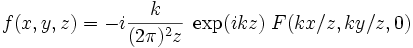 ,
,
l'amplitude en x, y, z est proportionnelle à la transformée de Fourier en 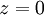 pour le vecteur d'onde
pour le vecteur d'onde 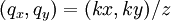 .
.
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.


 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité