Approximation BKW
En physique, l'approximation BKW Brillouin - Kramers - Wentzel est une méthode développée en 1926 qui permet d'étudier le régime semi-classique d'un dispositif quantique.
Recherche sur Google Images :
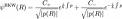
Source image : fr.wikipedia.org Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- ... et avec l'approximation de la phase stationnaire en utilisant la formule BKW... Elément matriciel ; Théorie quantique ; Fonction onde ; Espace phase... (source : cat.inist)
En physique, l'approximation BKW Brillouin[1] - Kramers [2] - Wentzel [3] est une méthode développée en 1926 qui permet d'étudier le régime semi-classique d'un dispositif quantique. La fonction d'onde est développée asymptotiquement au premier ordre de la puissance du quantum d'action  .
.
L'idée de base de la méthode BKW est que l'équation de Schrödinger se dérive de l'équation de propagation des ondes. On doit par conséquent retrouver la mécanique classique dans la limite  comme on retrouve l'optique géométrique quand la longueur d'onde
comme on retrouve l'optique géométrique quand la longueur d'onde  dans la théorie de l'optique ondulatoire.
dans la théorie de l'optique ondulatoire.
L'approximation BKW (pour les francophones) est aussi connue sous les initiales WKB (pour les anglophones), WKBJ, BWKJ et quelquefois WBK, BWK. Le J supplémentaire est pour le mathématicien Harold Jeffreys, qui a développé en 1923 une méthode générale d'approximation pour des équations différentielles linéaires du second ordre, qui inclut l'équation de Schrödinger à une dimension. Les trois physiciens BKW n'avaient apparemment pas eu connaissance de ce travail.
Formule à une dimension d'espace
De façon générale la fonction d'onde est mise sous la forme ansatz :
![\psi(\vec{r},t) \ = \ A(\vec{r},t) \ \exp \left[ \ \frac{i}{\hbar} \ S(\vec{r},t) \ \right]](illustrations/7e8f7b7f7bacc6a099f9cf9166efbdf1.png)
Les deux fonctions inconnues sont l'amplitude A et l'action S, l'une de ces deux fonctions est généralement reconnue comme «lentement variable». En fait seul le cas unidimentionnel où 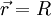 est utilisé, c'est ce cas que nous allons développer ici.
est utilisé, c'est ce cas que nous allons développer ici.
Formule BKW
Notons ψ la fonction d'onde, solution stationnaire de l'équation de Schrödinger, d'une particule de masse m se déplaçant dans le potentiel V (R) ;
L'approximation BKW consiste à écrire la fonction d'onde sous la forme
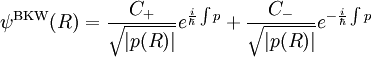
où 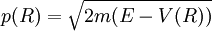 est l'impulsion locale de la particule.
est l'impulsion locale de la particule.
Sens physique
Notons le sens physique simple :
- Dans la région classiquement permise plus la particule va vite, plus sa probabilité de présence diminue. En effet à l'endroit où E > V (R) , la probabilité de présence | ψ | 2 sera proportionnelle à
 .
. - Dans la région classiquement interdite la probabilité de présence | ψ | 2 sera exponentiellement décroissante en
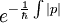 . En effet à l'endroit où E < V (R) , on a alors
. En effet à l'endroit où E < V (R) , on a alors 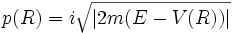 et le terme exponentiellement croissant sera généralement divergent et par conséquent non physique, la normalisation de la fonction d'onde impose alors C + = 0)
et le terme exponentiellement croissant sera généralement divergent et par conséquent non physique, la normalisation de la fonction d'onde impose alors C + = 0)
Domaine de validité
Le domaine de validité de l'approximation est le suivant
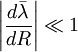 où
où 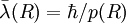 est la longueur d'onde de de Broglie dite réduite (divisée par 2 π)
est la longueur d'onde de de Broglie dite réduite (divisée par 2 π) - Une seconde condition, qui est fréquemment vérifiée, vient s'ajouter à celle-ci mais elle est rarement utilisée
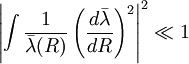
La première condition peut s'interpréter, en faisant apparaitre le produit 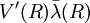 , comme une condition adiabatique, i. e. comme le fait que le potentiel V doit changer lentement sur des distances identiques à longueur d'onde
, comme une condition adiabatique, i. e. comme le fait que le potentiel V doit changer lentement sur des distances identiques à longueur d'onde 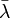 de la particule pour que celle-ci ait le temps de s'adapter au nouveau potentiel lors du mouvement.
de la particule pour que celle-ci ait le temps de s'adapter au nouveau potentiel lors du mouvement.
La seconde condition est plus complexe à interpréter mais elle indique qu'il faut être prudent si le potentiel V décroit trop lentement à l'infini.
Démonstration
En faisant apparaître les différents ordres du développement en puissance de 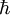 on pose
on pose
Ordre 0
En n'utilisant que σ0 dans ψ on obtient immédiatement
L'ordre 0, qui se nomme l'approximation classique, consiste à ne conserver aucun terme en 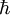 . On obtient
. On obtient 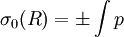 et donc
et donc
Ordre 1
L'ordre suivant est l'approximation B. K. W. elle-même.
En reprenant la formule précédente, avec 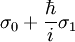 au lieu de σ0, et en ne gardant que les termes en
au lieu de σ0, et en ne gardant que les termes en  on obtient immédiatement 2σ'0σ'1 + σ''0 = 0
on obtient immédiatement 2σ'0σ'1 + σ''0 = 0
En utilisant la valeur de 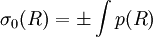 , on en déduit
, on en déduit 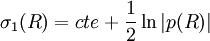 et finalement avec les deux signes envisageables de σ0
et finalement avec les deux signes envisageables de σ0
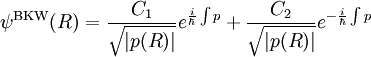
Ordre 2
Le calcul à l'ordre 2 apporte
où 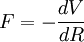 sert à désigner la force à laquelle est soumise la particule. Cette formule est rarement utilisée, mais en comparant avec la formule BKW, on voit que l'approximation BKW sera valide dans le cas où
sert à désigner la force à laquelle est soumise la particule. Cette formule est rarement utilisée, mais en comparant avec la formule BKW, on voit que l'approximation BKW sera valide dans le cas où 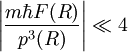 et
et 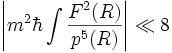
On préfère fréquemment réécrire ces conditions en utilisant F = pp'/ m ce qui amène aux conditions données auparavant qui sont :
Cas des points tournants classiques (vitesse nulle)
Les points où p (R) = 0 sont nommés les points de retournements classiques, en effet la vitesse v=p/m y est nulle, le mobile (ou la particule) fera demi-tour. En ces points la première condition n'est plus valable et l'approximation BKW est complètement fausse et il est par conséquent indispensable d'effectuer un traitement spécial pour ces points.
Au voisinage d'un tel point RC on peut écrire un développement limité du potentiel. En s'arrêtant au premier ordre où 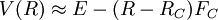 l'équation de Schrödinger devient une équation fonction d'Airy dont la solution est donnée par
l'équation de Schrödinger devient une équation fonction d'Airy dont la solution est donnée par ![\psi (R) = C_A {\rm Ai} \left[
\left( R_C- R
\right) \left(
{ 2 m F_C \over \hbarˆ2}
\right)ˆ{1/3} \right]](illustrations/89402175e37d22d45fc086ddff6aa85b.png)
Fonctions de connections
En utilisant les développement asymptotiques de la fonction d'Airy il est envisageable de les raccorder aux fonctions BKW de part et d'autre d'un point tournant.
Les raccordements de deux fonctions BKW s'en suivent et sont donnés par les lois suivantes.
- La fonction
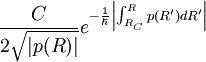 dans la région V (R) > E devient
dans la région V (R) > E devient 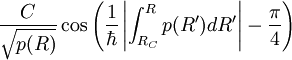 dans la région V (R) < E
dans la région V (R) < E - La fonction
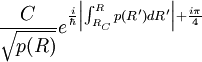 dans la région V (R) < E devient
dans la région V (R) < E devient 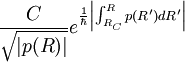 dans la région V (R) > E
dans la région V (R) > E
Signalons qu'il est préférable de ne pas extrapoler d'autres formules car les termes exponentiellement croissant et exponentiellement décroissant ne peuvent généralement cœxister dans la région classiquement interdite.
Approximation semi-classique uniforme
Notons aussi la formule de l'approximation semi-classique uniforme (ASU) valable dans l'ensemble des régions, donnée par :
![\psiˆ{\rm ASU} (R) = {C_4 \over \pi} \left[
{3 \hbarˆ2 \int_{R_C}ˆR p \over 2 pˆ3}
\right]ˆ{1/6}
{\rm Ai}\left[
\left(
{3 \int_{R_C}ˆR p \over 2 \hbar }
\right)ˆ{2/3}
\right]](illustrations/871a796afbc5e7f840c0e1df51c090c6.png)
Etats liés
L'une des applications principales de la théorie BKW concerne le calcul des fonctions d'onde dans un puits de potentiel.
En notant Rint le point tournant classique interne et Rext le point externe et en utilisant les formules de connections en ces deux points on s'aperçoit aisément que la somme des phases des cosinus doit être un multiple de π. On en déduit la condition de quantification, qui est en fait celle trouvée par Niels Bohr et Arnold Sommerfeld en 1913 dans l'ancienne théorie des quanta mais avec le 1/2 en plus 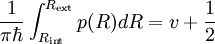 où v est le nombre de zéro de la fonction d'onde ψ du v+1 ème niveau lié du potentiel (théorème d'oscillation). L'approximation BKW s'écrit
où v est le nombre de zéro de la fonction d'onde ψ du v+1 ème niveau lié du potentiel (théorème d'oscillation). L'approximation BKW s'écrit
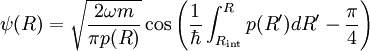
où on a normalisé à la fonction d'onde en négligeant la partie classiquement interdite et utilisant l'approximation de l'oscillation rapide du cosinus (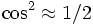 ).
).
ω sert à désigner la pulsation du mouvement classique et T est la période d'oscillation définies par 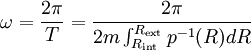
Plus v est grand, plus p l'est , et par conséquent plus l'approximation BKW sera valable (voir la première condition de validité). Il convient tout de même d'être soigneux pour les tous derniers niveaux du potentiel, car l'approximation BKW n'est plus valable (voir la seconde condition de validité).
Articles liés
- C. Cohen-Tannoudji, B. Diu et F. Laloë, Mécanique quantique [détail des éditions]
- Albert Messiah, Mécanique quantique [détail des éditions]
- Lev Landau et Evguéni Lifchitz, Physique théorique, tome 3 : Mécanique quantique, éd. MIR, Moscou [détail des éditions]
Notes
- ↑ Léon Brillouin La mécanique ondulatoire de Schrödinger; une méthode générale de resolution par approximations successives, Comptes rendus (Paris) 183 24-26 (1926)
- ↑ H. A. Kramers Wellenmechanik und halbzahlige Quantisierung, Z. Physik. 39 828-840 (1926)
- ↑ Gregor Wentzel Eine Verallgemeinerung der Quantenbedingungen für die Zwecke der Wellenmechanik, Z. Physik. 38 518-529 (1926).
Aspects récents
- Harald Siegfried Friedrich ; Theoretical Atomic Physics, Springer; 3 edition (October 6, 2005), ISBN-13 : 978-3540256441
- André Voros ; Spectre de l'équation de Schrödinger et méthode BKW, notes de cours (Orsay - 1980/1981), Publications Mathématiques de l'Université Paris-Sud Orsay 81-09 (1981). pdf.
- André Voros ; De la théorie BKW exacte vers la théorie des perturbations singulières (II) , AOKI T., KOIKE T., MAJIMA H., TAKEI Y., TOSE N., eds. (Springer-Verlag, Berlin) Mondial Conference on Algebraic Analysis of Differential Equations (from Microlocal Analysis to Exponential Asymptotics), in honor of Prof. Takahiro Kawai on the occasion of his sixtieth birthday (invitation), Kyoto University, Kyoto, Japan, July 7-14 2005. ArXiv : math-ph/0603043.
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 12/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

![\left[ -{ \hbarˆ2 \over 2 m } {dˆ2 \over d Rˆ2} + V(R) \right] \psi(R) = E \psi(R)](illustrations/3eacd415b13142f61ff90c53311b87c7.png)
![\psi(R) = eˆ{\frac{i}{ \hbar} \left[
\sigma_0 (R) + {\hbar \over i} \sigma_1 (R) + \left(\frac{\hbar}{
i}\right)ˆ2
\sigma_2 (R) + \cdots
\right]}](illustrations/0dd10a9cb5d3f88e250d903bef808b3d.png)
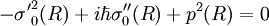
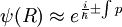
![\psi (R) = {C'_1 \over \sqrt{ |p(R) | } }
\left[
1 - {i m \hbar \over 4} { F(R) \over pˆ3(R) } -
{i mˆ2 \hbar \over 8} \int { Fˆ2 \over pˆ5 }
\right]
eˆ{ {i \over \hbar} \int
p } + {C'_2 \over \sqrt{ |p(R) | } }
\left[
1 + {i m \hbar \over 4} { F(R) \over pˆ3(R) } +
{i mˆ2 \hbar \over 8} \int { Fˆ2 \over pˆ5 }
\right]
eˆ{- {i \over \hbar} \int
p }](illustrations/9cbf8c4b5c826c543e61dc842962ba2d.png)
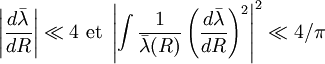

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité