Théorie des perturbations
D'un point de vue heuristique, la théorie des perturbations est une méthode mathématique générale qui sert à trouver une solution approchée d'une équation mathématique dépendante d'un paramètre λ quand la solution de l'équation, correspondant à la valeur λ = 0,...

Catégories :
Équation - Méthode mathématique de la physique - Mécanique céleste - Mécanique quantique - Physique quantique
Recherche sur Google Images :
Source image : depire.free.fr Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- La théorie des perturbations est une méthode générale (valable quelque soit la forme de l'énergie potentiel) de résolution approchée de l'équation de ... (source : opus.grenet)
- Une solution à cette équation par la méthode des caractéristiques apportés des solutions.... un premier terme représentant un couplage visqueux décrivant la... (source : publications.european-patent-office)
- Méthode selon la revendication 2, dans laquelle ledit premier terme est obtenu en .... Une solution à cette équation par la méthode des caractéristiques... (source : freepatentsonline)
D'un point de vue heuristique, la théorie des perturbations est une méthode mathématique générale qui sert à trouver une solution approchée d'une équation mathématique (Eλ) dépendante d'un paramètre λ quand la solution de l'équation (E0) , correspondant à la valeur λ = 0, est connue précisément. L'équation mathématique (Eλ) peut être une équation algébrique, une équation différentielle, une équation aux valeurs propres, ... La méthode consiste à chercher la solution approchée de l'équation (Eλ) sous la forme d'un développement en série des puissances du paramètre λ, cette solution approchée étant supposé être une approximation d'autant meilleure de la solution exacte, mais inconnue, que la valeur absolue du paramètre λ est plus «petite».
Dès le début du XVIIIe siècle, la théorie des perturbations a été utilisée par les astronomes pour les besoins de la mécanique céleste : en effet, les équations différentielles décrivant un dispositif de N corps en interaction gravitationnelle n'a pas de solution exacte générale [1] pour 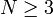 . Cet aspect de la théorie des perturbations a été synthétisé à la fin du XIXe siècle dans les ouvrages classiques de Laplace[2], Tisserand[3] et Poincaré[4], avant de connaitre de nouveaux développements dans la seconde moitié du XXe siècle avec l'avènement en 1954 de la «théorie KAM», du nom de ses trois concepteurs : Kolmogorov, Arnold et Moser.
. Cet aspect de la théorie des perturbations a été synthétisé à la fin du XIXe siècle dans les ouvrages classiques de Laplace[2], Tisserand[3] et Poincaré[4], avant de connaitre de nouveaux développements dans la seconde moitié du XXe siècle avec l'avènement en 1954 de la «théorie KAM», du nom de ses trois concepteurs : Kolmogorov, Arnold et Moser.
La méthode a d'autre part été abondamment utilisée au XXe siècle pour les besoins de la physique quantique, en premier lieu en mécanique quantique non relativiste, puis en théorie quantique des champs perturbative.
Convergence de la série perturbative ?
On a vu qu'on cherchait ici la solution approchée de l'équation (Eλ) sous la forme d'un développement en série des puissances du paramètre λ ; la question de la convergence de cette série se pose alors. Ce problème a été réglé pour l'astronomie par Poincaré en 1892 : la «série» de perturbation doit être comprise mathématiquement comme un développement asymptotique au voisinage de zéro, et non comme une série ordinaire convergente uniformément. Le chapitre VIII de la Mécanique céleste de Poincaré[5] débute par le commentaire suivant :
«II y a entre les géomètres et les astronomes une sorte de malentendu au sujet de la signification du mot convergence. Les géomètres préoccupés de l'idéale rigueur et fréquemment trop indifférents à la longueur de calculs inextricables dont ils conçoivent la possibilité, sans songer à les entreprendre effectivement, disent qu'une série est convergente lorsque la somme des termes tend vers une limite déterminée, quand même les premiers termes diminueraient particulièrement lentement. Les astronomes, au contraire, ont coutume de dire qu'une série converge lorsque les 20 premiers termes, par exemple, diminuent particulièrement rapidement, quand même les termes suivants devraient croître indéfiniment.
Ainsi, pour prendre un exemple simple, considérons les deux séries qui ont pour terme général :
Les géomètres diront que la première converge, et même qu'elle converge rapidement, parce que le millionième terme est bien plus petit que le 999 999 ème ; mais ils regarderont la seconde comme divergente, parce que le terme général peut croître au delà de toute limite.
Les astronomes, au contraire, regarderont la première série comme divergente, parce que les 1000 premiers termes vont en croissant ; et la seconde comme convergente, parce que les 1000 premiers termes vont en décroissant et que cette décroissance est en premier lieu particulièrement rapide.
Les deux règles sont légitimes : la première, dans les recherches théoriques ; la seconde, dans les applications numériques. Toutes deux doivent régner, mais dans deux domaines scindés et dont il importe de bien connaître les frontières. »
Pour conclure cette discussion qualitative sur la convergence, le mathématicien Jean-Pierre Ramis précise[6] :
«On peut ainsi parler de séries convergentes «au sens des géomètres» ou «au sens des astronomes». Notons que quasiment, dans les applications, on constate que, presque toujours, les séries convergentes au sens des astronomes ont un terme général qui croît particulièrement vite après avoir en premier lieu diminué. Ainsi, ce que Poincaré envisageait comme possibilité est en fait la règle.»
C'est d'ailleurs ce qui fait l'efficacité pratique de la théorie des perturbations en physique théorique : il suffit le plus fréquemment de calculer les quelques premiers termes du développement asymptotique - ceux qui semblent commencer par converger - pour obtenir une très bonne approximation du résultat exact inconnu. Ainsi, dans le cadre de l'électrodynamique quantique, Dyson a montré en 1948 que la série perturbative était divergente, tandis que la prise en compte des trois ou quatre premiers termes uniquement donnent des prédictions théoriques en accord remarquable avec les résultats expérimentaux.
Notons qu'il existe certaines procédures de «sommation» qui permettent de donner un sens à certaines séries divergentes, comme par exemple la sommation de Borel ou l'approximant de Padé.
Considérons à titre d'exemple l'équation différentielle du premier ordre suivante :
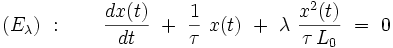 |
Dans cette équation, t représente le temps, τ un paramètre fixé homogène à un temps, L0 un paramètre fixé homogène à une longueur, et λ le paramètre de perturbation, sans dimensions. On cherche à déterminer la fonction x (t) inconnue, homogène à une longueur, et vérifiant la condition initiale : à l'instant t = 0, on a : x (0) = X0.
Théorie des perturbations au premier ordre
Le problème de départ de la théorie des perturbations est l'équation différentielle (E0) correspondant à la valeur λ = 0 :
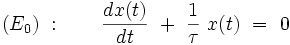 |
dont la solution analytique exacte est bien connue :
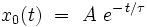 |
où A est une constante, pour le moment inconnue. Illustrons la méthode de perturbations en nous limitant pour simplifier au premier ordre dans le développement en série des puissances du paramètre λ ; on cherche par conséquent la solution approchée sous la forme :
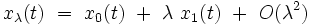 |
où x1 (t) est une fonction inconnue, à déterminer. On injecte cette expression dans l'équation différentielle exacte (Eλ) . En se limitant aux termes du premier ordre inclus et en utilisant le fait que x0 (t) est la solution exacte de (E0) , on obtient la solution physique approchée au premier ordre :
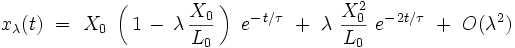 |
On injecte le développement dans l'équation différentielle exacte (Eλ) . En se limitant au termes du premier ordre inclus et en utilisant le fait que x0 (t) est la solution exacte de (E0) , on obtient l'équation suivante pour la fonction x1 (t) :
![\lambda \ \left[ \ \frac{dx_1(t)}{dt} \ + \ \frac{1}{\tau} \ x_1(t) \ \right] \ + \ \lambda \ \frac{xˆ2_0(t)}{\tau \, L_0} \ = \ 0](illustrations/4411e593eb03638b074d432a00c46974.png)
On a omis le terme O (λ2) de reste de Landau pour simplifier l'écriture. Cette équation se réécrit explicitement :
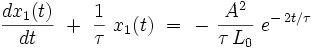
Cette équation différentielle admet une solution analytique exacte de la forme :
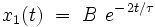
où B est une constante, qu'on détermine en introduisant l'expression de x1 (t) dans l'équation différentielle. On obtient explicitement :
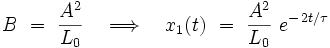
d'où la solution générale de (Eλ) approchée au premier ordre.
Comparaison avec la solution exacte
On peut démontrer ici que l'équation différentielle (Eλ) vérifiant la condition initiale : x (0) = X0 admet pour toute les valeurs du paramètre λ la solution exacte suivante :
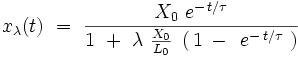 |
Un développement limité de cette expression au premier ordre en λ donne explicitement la solution approchée déterminée au paragraphe précédent par la théorie des perturbations au premier ordre :
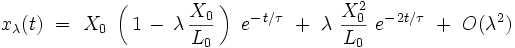 |
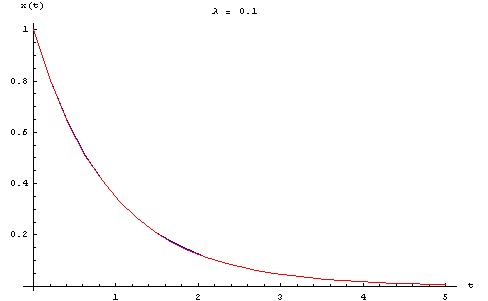
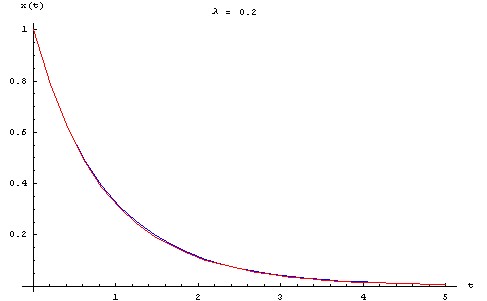
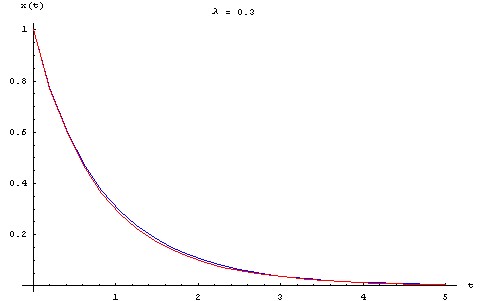
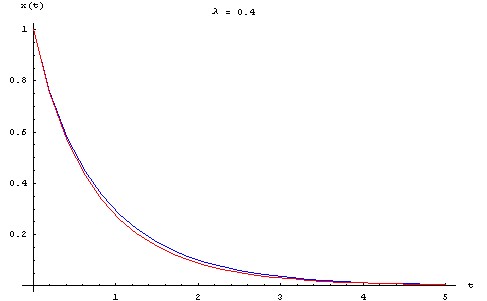
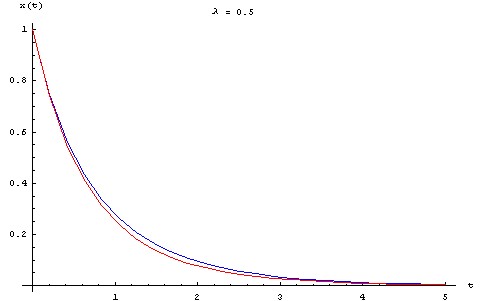
Pour visualiser l'écart entre la solution approchée et la solution exacte, on trace ci-dessous les graphes des deux fonctions pour une série de valeurs de λ allant de 0.1 à 0.5, en prenant : X0 = L0 = 1 m, τ = 1 s.
- en bleu, la solution exacte.
- en rouge, la solution approchée au premier ordre.
Définition
L'oscillateur de Duffing satisfait à l'équation différentielle du second ordre suivante :
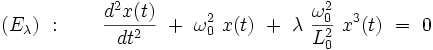 |
Dans cette équation, t représente le temps, ω0 un paramètre fixé homogène à une pulsation, c'est-à-dire l'inverse d'un temps. L0 est un paramètre fixé homogène à une longueur, et λ le paramètre de perturbation, sans dimensions. On cherche à déterminer la fonction x (t) inconnue, homogène à une longueur, et vérifiant les conditions initiales : à l'instant t = 0, on a : x (0) = X0 et 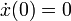 .
.
Interprétation physique
On peut interpréter cette équation différentielle comme la loi de la dynamique de Newton d'une particule de masse m soumise à une force dérivant d'une énergie potentielle V (x) :
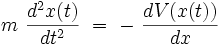 |
où le potentiel V (x) quartique s'écrit :
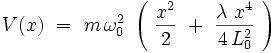 |
Caractère borné du mouvement
Pour l'ensemble des valeurs de λ positives ou nulles, V (x) représente un puits de potentiel. La conservation de l'énergie mécanique totale E de la particule :
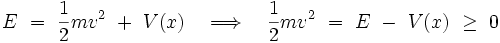 |
entraine tandis que le mouvement est borné dans un intervalle ![[ \, x_1, \, x_2 \, ]](illustrations/67ad3f6577fc6223cabaa626311bee4c.png) , où les points tournants x1 et x2 sont les deux solutions réelles de l'équation :
, où les points tournants x1 et x2 sont les deux solutions réelles de l'équation :
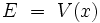 |
Ordre zéro : l'oscillateur harmonique
Le problème de départ de la théorie des perturbations est l'équation différentielle (E0) correspondant à la valeur λ = 0 :
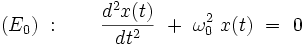 |
Cette équation est par définition un oscillateur harmonique de pulsation ω0, dont la solution analytique exacte est bien connue :
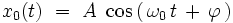 |
où A et 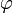 sont deux constantes, pour le moment inconnues.
sont deux constantes, pour le moment inconnues.
Théorie de perturbation naïve au premier ordre
On cherche la solution approchée sous la forme :
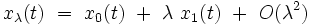 |
où x1 (t) est une fonction inconnue, à déterminer. On injecte cette expression dans l'équation différentielle exacte (Eλ) . En se limitant au termes du premier ordre inclus et en utilisant le fait que x0 (t) est la solution exacte de (E0) , on obtient l'expression au premier ordre de la théorie de perturbation :
![x_{\lambda}(t) \ = \ X_0 \ \cos \left( \omega_0 t \right) \ + \ \lambda \ \left[ \frac{X_0ˆ3}{32 \, L_0ˆ2} \left[ \, \cos \left( 3 \omega_0 t \right) \, - \, \cos \left( \omega_0 t \right) \, \right] \ + \ \frac{3 \, X_0ˆ3}{8 \, L_0ˆ2} \ \omega_0 t \ \sin \left( \omega_0 t \right) \ \right] \ + \ O(\lambdaˆ2)](illustrations/f3eaccc49a1b0d8bf5cc5c86e785ce10.png) |
On injecte le développement dans l'équation différentielle exacte (Eλ) . En se limitant au termes du premier ordre inclus et en utilisant le fait que x0 (t) est la solution exacte de (E0) , on obtient l'équation suivante pour la fonction x1 (t) :
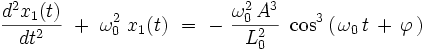
On utilise l'identité trigonométrique suivante :
![\cosˆ3 \alpha \ = \ \frac{1}{4} \ \left[ \ 3 \ \cos \alpha \ + \ \cos (3 \alpha ) \ \right]](illustrations/5b2a184929fbf0a772ceea144ec7919f.png)
d'où l'équation différentielle pour la fonction x1 (t) :
![\frac{dˆ2x_1(t)}{dtˆ2} \ + \ \omega_0ˆ2 \ x_1(t) \ = \ - \ \frac{\omega_0ˆ2 \, Aˆ3}{4 \, L_0ˆ2} \ \left[ \ 3 \ \cos \left( \, \omega_0 \, t \, + \, \varphi \, \right) \ + \ \cos \left( \, 3 \, \omega_0 \, t \, + \, 3 \, \varphi \, \right) \ \right]](illustrations/3de9fc20efeb35f92b712418ff9cf150.png)
On peut démontrer que cette équation différentielle possède la solution générale exacte suivante :
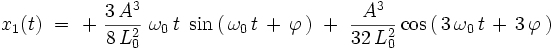
On a par conséquent pour la fonction inconnue :
![x_{\lambda}(t) \ = \ A \ \cos \left( \, \omega_0 \, t \, + \, \varphi \, \right) \ + \ \lambda \ \left[ \, + \, \frac{3 \, Aˆ3}{8 \, L_0ˆ2} \ \omega_0 \, t \ \sin \left( \, \omega_0 \, t \, + \, \varphi \, \right) \ + \ \frac{Aˆ3}{32 \, L_0ˆ2} \cos \left( \, 3 \, \omega_0 \, t \, + \, 3 \, \varphi \, \right) \, \right] \ + \ O(\lambdaˆ2)](illustrations/0ab874c5483abc620ed7c88af71a6e98.png)
L'application des conditions initiales : à l'instant t = 0, on a : x (0) = X0 et 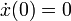 amènent au dispositif de deux équations à deux inconnues :
amènent au dispositif de deux équations à deux inconnues :
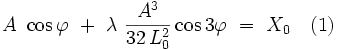
![- \ A \ \omega_0 \ \sin \varphi \ + \ \lambda \ \left[ \ \frac{3 \, \omega_0 \, Aˆ3}{8 \, L_0ˆ2} \ \sin \varphi \ - \ \frac{3 \omega_0 \, Aˆ3}{32 \, L_0ˆ2} \ \ \sin 3 \varphi \ \right] \ = \ 0 \quad (2)](illustrations/6e6e85c0fe9609081aefd5bbee1f4f7a.png)
En utilisant la formule trigonométrique :
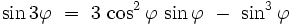
dans l'équation (2), on montre que : 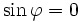 , par conséquent que :
, par conséquent que : 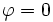 . On reporte ensuite ce résultat dans l'équation (1), ce qui donne :
. On reporte ensuite ce résultat dans l'équation (1), ce qui donne :
![A \ + \ \lambda \ \frac{Aˆ3}{32 \, L_0ˆ2} \ = \ X_0 \quad \Longrightarrow \quad A \ = \ X_0 \ \left[ \, 1 \, - \, \frac{\lambda \, X_0ˆ2}{32 \, L_0ˆ2} \, \right] \ + \ O(\lambdaˆ2)](illustrations/806118cce2f2402e56e36fd80e354145.png)
On en déduit l'expression au premier ordre de la théorie de perturbation.
Apparition d'un terme séculaire
On constate que la perturbation contient un terme proportionnel au temps :
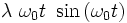 |
Ce terme non borné est nommé terme séculaire, du mot latin sæculum qui veut dire siècle. En effet, pour les temps 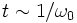 , la perturbation est bien d'ordre λ, c'est-à-dire petite. Par contre, pour des temps plus longs de l'ordre de
, la perturbation est bien d'ordre λ, c'est-à-dire petite. Par contre, pour des temps plus longs de l'ordre de 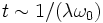 , la perturbation devient d'ordre 1 et n'est plus petite ; le problème devient toujours pire pour des temps toujours plus longs :
, la perturbation devient d'ordre 1 et n'est plus petite ; le problème devient toujours pire pour des temps toujours plus longs : 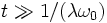 . Or nous savons que le mouvement réel est borné, par conséquent que xλ (t) ne peut pas croître indéfiniment : notre théorie des perturbations «naïve» n'est par conséquent plus valide.
. Or nous savons que le mouvement réel est borné, par conséquent que xλ (t) ne peut pas croître indéfiniment : notre théorie des perturbations «naïve» n'est par conséquent plus valide.
Dans le cadre de l'astronomie, la présence de ces termes séculaires empêchent d'étudier le futur à long terme des trajectoires planétaires, l'unité de temps caractéristique du problème étant le siècle.
Méthode de Lindstedt
Lindstedt a proposé en 1882 une méthode qui, pour certaines équation différentielles, permet d'éliminer ces termes séculaire[7], [8]. On l'appelle aussi méthode de Lindstedt-Poincaré, Poincaré ayant démontré que les séries introduites par Lindstedt devaient être interprétées comme des expressions asymptotiques[9], [10], [11].
L'idée de Lindstedt est la suivante : occasionnellemen, les termes séculaires peuvent être dus au fait qu'on développe incorrectement les expressions. A titre d'exemple, supposons que le résultat exact soit :
![x_{\lambda}(t) \ = \ X_0 \ \cos \left[ \, \left( 1 + \lambda \right) \, \omega_0 t \, \right]](illustrations/3e40f6e950e4d47ae12f67b8632b3c78.png) |
Cette expression clairement bornée développée au premier ordre en λ donne :
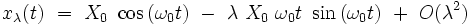 |
et il apparait un terme séculaire non borné ! On voit que la solution exacte est en fait une fonction de la pulsation :
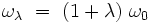 |
qui est un peu différente de la pulsation d'origine ω0 du problème. Lindstedt va utiliser cette remarque de façon systématique.
Principe de la méthode de Lindstedt
La méthode de Lindstedt ne s'applique que pour les équations différentielles du type suivant :
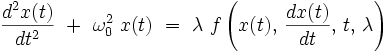 |
où f est une fonction paire de x et impaire de 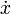 qui est qui plus est soit périodique en t, soit indépendante de t. La méthode consiste à faire un changement d'échelle de temps en introduisant une nouvelle variable s sans dimensions définie par le développement en série :
qui est qui plus est soit périodique en t, soit indépendante de t. La méthode consiste à faire un changement d'échelle de temps en introduisant une nouvelle variable s sans dimensions définie par le développement en série :
![s \ = \ \left[ \ \omega_0 \ + \ \lambda \omega_1 \ + \ \lambdaˆ2 \omega_2 \ + \ \dots \ \right] \ t](illustrations/2e8d1def18d5e8e327e0db5c9cea5fd9.png) |
Dans cette expression, les valeurs numériques des constantes inconnues 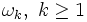 devront être choisies pour faire disparaitre les termes séculaires de la série perturbative de la solution approchée à l'ordre désiré.
devront être choisies pour faire disparaitre les termes séculaires de la série perturbative de la solution approchée à l'ordre désiré.
Illustrons la méthode dans le paragraphe suivant avec l'oscillateur de Duffing.
Exemple : l'oscillateur de Duffing au premier ordre
On a vu plus haut que l'équation différentielle de l'oscillateur de Duffing s'écrivait :
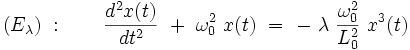 |
Faisons le changement d'échelle de temps 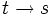 et définissons la nouvelle fonction inconnue y de la variable spar :
et définissons la nouvelle fonction inconnue y de la variable spar :
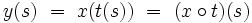 |
La règle de Leibniz de dérivation en chaine donne pour la dérivée première :
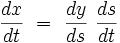 |
et pour la dérivée seconde :
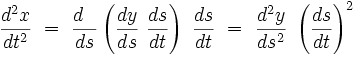 |
Comme on a au premier ordre :
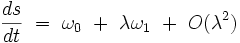 |
on obtient pour les dérivées :
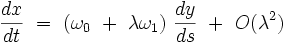 |
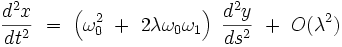 |
L'équation différentielle de Duffing devient au premier ordre :
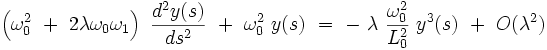 |
Introduisons désormais dans cette équation différentielle le développement au premier ordre de la solution :
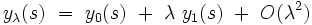 |
Il vient en développant selon les puissances de λ :
![\omega_0ˆ2 \left(\frac{dˆ2y_0}{dsˆ2} + y_{0} \right) \ + \ \lambda \left[ \omega_0ˆ2 \frac{dˆ2y_1}{dsˆ2} + 2 \omega_0 \omega_1 \frac{dˆ2y_0}{dsˆ2} + \omega_0ˆ2 y_1 + \frac{\omega_0ˆ2}{L_0ˆ2} \ y_0ˆ3 \right] \ = \ 0 + O(\lambdaˆ2)](illustrations/4be2eba910fb3ebf97be3d0c08c81abb.png) |
On a par conséquent le dispositif de deux équations différentielle :
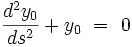 |
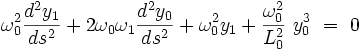 |
La première a pour solution générale : 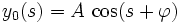 où A et
où A et 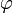 sont deux constantes. On reporte alors cette expression dans la seconde équation différentielle, et on obtient pour la première correction y1 (s) :
sont deux constantes. On reporte alors cette expression dans la seconde équation différentielle, et on obtient pour la première correction y1 (s) :
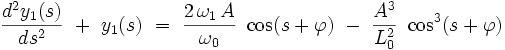 |
On réutilise la formule trigonométrique :
![\cosˆ3 \alpha \ = \ \frac{1}{4} \ \left[ \ 3 \ \cos \alpha \ + \ \cos (3 \alpha ) \ \right]](illustrations/5b2a184929fbf0a772ceea144ec7919f.png) |
d'où l'équation différentielle pour la fonction y1 (s) :
![\frac{dˆ2y_1(s)}{dsˆ2} \ + \ y_1(s) \ = \ \left[ \ \frac{2 \, \omega_1}{\omega_0} \ - \ \frac{3 \, Aˆ3}{4L_0ˆ2} \right] \ \cos (s + \varphi) \ - \ \frac{Aˆ3}{4L_0ˆ2} \ \cos (3s + 3 \varphi )](illustrations/b07e621a476d09ddc41b80eb3f51fa68.png) |
Il suffit alors d'annuler le cœfficient devant le terme en 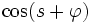 en posant :
en posant :
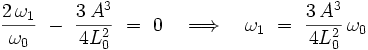 |
On obtient alors l'équation différentielle finale pour la fonction y1 (s) :
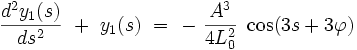 |
Cette équation différentielle admet une solution générale bornée sans terme séculaire :
A suivre...
Bibliothèque virtuelle
- Nils Berglund ; Perturbation theory of dynamical systems (2001). Disponible sur l'ArXiv : math. HO/0111178.
Ouvrages de référence
- Ali H. Nayfeh ; Perturbation Methods, John Wiley & Sons (New York-1973), réédité dans la collection : Wiley Classics Library (2000), ISBN 0-471-39917-5.
- Ali H. Nayfeh ; Introduction to Perturbation Techniques, John Wiley & Sons (New York-1981), ISBN 0-471-31013-1.
- E. John Hinch ; Perturbation Methods, Cambridge Texts in Applied Mathematics, Cambridge University Press (1991), ISBN 0521378974.
- Donald R. Smith ; Singular-Perturbation Theory : An Introduction with Applications, Cambridge University Press (1985), ISBN 0-521-30042-8.
Articles de revue
- Donald R. Smith ; The Multivariable Method in Singular Perturbation Analysis, SIAM Review 17 (2) (1975), 221-273.
- A. B. Vasilieva ; On the Development of Singular Perturbation Theory at Moscow State University and Elsewhere, SIAM Review 36 (3) (1994), 440-452.
Applications à la mécanique céleste
La mécanique hamiltonienne a connu une avancée spectaculaire en 1954 avec l'avènement de la «théorie KAM». Les références ci-dessous sont par conséquent classées selon cet évènement.
Théorie pré-KAM
- Pierre-Simon Laplace ; Traité de mécanique céleste, Editions Jacques Gabay (1990). Réédition d'un ouvrage classique de la fin du XIXe siècle, en 4 volumes. Niveau second cycle universitaire. Cet ouvrage est disponible en fac-similé sur Gallica disponible sur Gallica.
- François-Félix Tisserand ; Traité de mécanique céleste, Editions Jacques Gabay (1990). Réédition d'un ouvrage classique de la fin du XIXe siècle, en 4 volumes. Niveau second cycle universitaire. Cet ouvrage est disponible en fac-similé sur Gallica.
- Henri Poincaré ; Leçons de mécanique céleste, 3 tomes, (1905-1910), réédité par Jacques Gabay, Paris (2003). Une somme de référence, par le grand mathématicien qui a tant contribué au sujet. Niveau second cycle universitaire. Cet ouvrage est disponible en fac-similé sur Gallica : Tome I, Tome II, Tome III.
- Anders Lindstedt ; Abh. K. Akad. Wiss. St. Petersburg 31 (1882), 4.
- Anders Lindstedt ; Sur la forme des expressions des distances mutuelles dans le problème des trois corps, Comptes-Rendus de l'Académie des Sciences 97 (1883) 1276 et 1353. Ces deux notes sont disponibles en fac-similé sur Gallica.
- Henri Poincaré ; Sur les séries de M. Lindstedt, Comptes-Rendus de l'Académie des Sciences 108 (1889) 21-24. Cette note est disponible en fac-similé sur Gallica.
- Henri Poincaré ; Sur l'application de la méthode de M. Lindstedt au problème des trois corps, Comptes-Rendus de l'Académie des Sciences 114 (1892) 1305-1309. Cette note est disponible en fac-similé sur Gallica.
Théorie post-KAM
- Florin Diacu & Philip Holmes ; Celestial Encounters - The Origin of Chaos & Stability, Princeton University Press (1996). ].
- V. I. Arnold, V. V. Kozlov & A. I. Neishtadt ; Mathematical Aspects of Classical & Celestial Mechanics, Springer-Verlag (2e édition-1997)
- Bibliographie de l'article Mécanique céleste
Références
- ↑ Il existe en fait une solution exacte du problème des trois corps découverte par Sundman (1909). Cette solution exacte, sous la forme d'un développement en série formelle, n'est en pratique pas exploitable, car si la série converge bien «au sens des géomètres», elle le fait si lentement que cela rend son pouvoir prédictif quasi-nul. Lire : Malte Henkel ; Sur la solution de Sundman du problème des trois corps, Philosophia Scientiæ 5 (2) (2001) pp. 161-184. Texte complet disponible sur l'ArXiv : physics/0203001.
- ↑ Pierre-Simon Laplace ; Traité de mécanique céleste, Editions Jacques Gabay (1990). Réédition d'un ouvrage classique de la fin du XIXe siècle, en 4 volumes. Niveau second cycle universitaire. Cet ouvrage est disponible en fac-similé sur Gallica.
- ↑ François-Félix Tisserand ; Traité de mécanique céleste, Editions Jacques Gabay (1990). Réédition d'un ouvrage classique de la fin du XIXe siècle, en 4 volumes. Niveau second cycle universitaire. Cet ouvrage est disponible en fac-similé sur Gallica.
- ↑ Henri Poincaré ; Leçons de mécanique céleste, 3 tomes, (1905-1910), réédité par Jacques Gabay, Paris (2003). Une somme de référence, par le grand mathématicien qui a tant contribué au sujet. Niveau second cycle universitaire. Cet ouvrage est disponible en fac-similé sur Gallica : Tome I, Tome II, Tome III.
- ↑ Henri Poincaré ; Les méthodes nouvelles de la mécanique céleste, Gauthier-Villars (1892).
- ↑ Jean-Pierre Ramis, Séries divergentes et théories asymptotiques, Journées X-UPS (1991).
- ↑ Anders Lindstedt ; Abh. K. Akad. Wiss. St. Petersburg 31 (1882), 4.
- ↑ Anders Lindstedt ; Sur la forme des expressions des distances mutuelles dans le problème des trois corps, Comptes-Rendus de l'Académie des Sciences 97 (1883) 1276 et 1353. Ces deux notes sont disponibles en fac-similé sur Gallica.
- ↑ Henri Poincaré ; Sur les séries de M. Lindstedt, Comptes-Rendus de l'Académie des Sciences 108 (1889) 21-24. Cette note est disponible en fac-similé sur Gallica.
- ↑ Henri Poincaré ; Sur l'application de la méthode de M. Lindstedt au problème des trois corps, Comptes-Rendus de l'Académie des Sciences 114 (1892) 1305-1309. Cette note est disponible en fac-similé sur Gallica.
- ↑ Henri Poincaré ; Leçons de mécanique céleste, 3 tomes, (1905-1910), réédité par Jacques Gabay, Paris (2003). Une somme de référence, par le grand mathématicien qui a tant contribué au sujet. Niveau second cycle universitaire. Cet ouvrage est disponible en fac-similé sur Gallica : Tome I, Tome II, Tome III.
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.
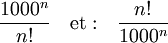

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité