Nombre quantique secondaire
En physique, en mécanique quantique, dans le modèle de Bohr, le nombre quantique secondaire, aussi nommé nombre quantique azimutal est le deuxième des quatre nombres qui définissent l'état quantique d'un électron.
Recherche sur Google Images :
Source image : fr.wikipedia.org Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- Le nombre quantique secondaire : l. Ce nombre est aussi nommé nombre quantique azimutal ou de moment angulaire l. l peur prendre les valeurs l= 0, 1, 2, …... (source : chemphys.u-strasbg)
- Nombre quantique secondaire (ou azimutal ou orbital) l o 2.3 Nombre quantique tertiaire (ou magnétique) m o 2.4 Nombre quantique de spin s... (source : roselynegigot.blogspot)
- Le nombre quantique secondaire ou azimutal quantifie la norme du vecteur... valeurs du nombre quantique secondaire l selon le tableau ci-contre :... (source : lpmc.univ-montp2)
En physique, en mécanique quantique, dans le modèle de Bohr, le nombre quantique secondaire, aussi nommé nombre quantique azimutal est le deuxième des quatre nombres qui définissent l'état quantique d'un électron. On considère généralement qu'il définit une sous-couche électronique, le nombre quantique principal n définissant la couche. Il est noté l (L minuscule) et détermine la géométrie de l'orbitale atomique.
Pour un nombre quantique principal n donné, le nombre quantique secondaire peut prendre l'ensemble des valeurs entières de 0 à (n-1)
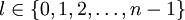 ou
ou 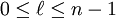
Nom et forme des orbitales
| valeur de l | lettre | nom | nb max e– | forme |
|---|---|---|---|---|
| 0 | s | sharp | 2 | sphère |
| 1 | p | principal | 6 | 2 haltères |
| 2 | d | diffuse | 10 | 4 haltères |
| 3 | f | fundamental | 14 | 8 haltères |
| 4 | g | 18 | ||
| 5 | h | 22 | ||
| 6 | i | 26 |
Moment angulaire de l'électron
Le nombre quantique secondaire quantifie le moment angulaire L de l'électron auquel il est lié par la relation :
où 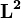 est l'opérateur de moment angulaire,
est l'opérateur de moment angulaire, 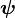 la fonction d'onde et
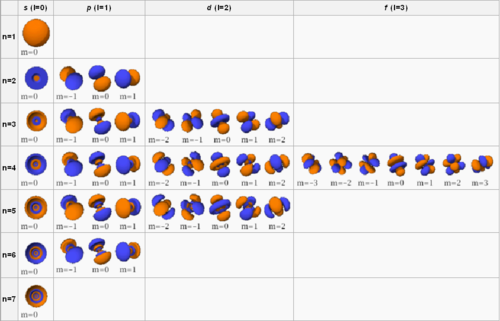
la fonction d'onde et 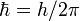 la constante de Planck réduite.
la constante de Planck réduite.
Voir aussi
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

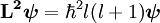

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité