Spin
Le spin est une propriété quantique intrinsèque associée à chaque particule, qui est caractéristique de la nature de la particule, tout comme sa masse et sa charge électrique.
Recherche sur Google Images :
Source image : irfu.cea.fr Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- Le spin est une propriété quantique intrinsèque...... Cette vision classique d'une «rotation propre» de la particule est en fait trop naïve ; en effet :... (source : techno-science)
Le spin est une propriété quantique intrinsèque associée à chaque particule, qui est caractéristique de la nature de la particule, tout comme sa masse et sa charge électrique. Elle sert à caractériser le comportement de la particule sous l'effet de la symétrie de rotation de l'espace.
Définition simplifiée
La notion de spin sert à classer mathématiquement la façon dont se transforment les objets sous l'effet des rotations de l'espace à trois dimensions. De façon générale, un objet possède un spin 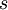 s'il est invariant sous une rotation d'angle
s'il est invariant sous une rotation d'angle 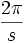 . Par exemple :
. Par exemple :
- Un objet sans symétrie spécifique, par exemple une carte à jouer représentant un trois de trèfle, possède un spin 1 car il est indispensable d'effectuer une rotation de
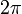 (un tour complet) pour qu'il se retrouve dans sa position de départ.
(un tour complet) pour qu'il se retrouve dans sa position de départ. - Un objet possédant légèrement plus de symétrie, comme une dame de pique par exemple, possède un spin 2 car pour qu'elle revienne à sa position de départ, on peut se contenter de lui faire effectuer une rotation de
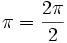 (un demi-tour).
(un demi-tour). - Une étoile à cinq branches possède un spin 5 car il est suffisant de lui faire faire une rotation de
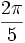 .
. - Un objet totalement symétrique, comme une sphère par exemple, est invariante par rotation de n'importe quel angle. La définition simplifiée qu'on a donnée est complexe à appliquer dans ce cas mais mathématiquement il est naturel de dire qu'un tel objet possède un spin illimité.
Remarquons que d'ordinaire, puisqu'une rotation d'angle 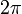 est identique à l'identité, il semblerait que tout objet soit de spin entier car dans le pire des cas un objet devrait toujours être semblable à lui-même sous une rotation d'angle
est identique à l'identité, il semblerait que tout objet soit de spin entier car dans le pire des cas un objet devrait toujours être semblable à lui-même sous une rotation d'angle 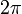 . Néenmoins l'analyse mathématique rigoureuse du groupe des rotations montre une structure subtile autorise certains objets d'avoir un spin demi-entier. Pour de tels objets, faire un tour complet sur eux-mêmes n'est pas suffisant pour les faire revenir à leur position de départ mais il est indispensable d'effectuer une rotation d'angle
. Néenmoins l'analyse mathématique rigoureuse du groupe des rotations montre une structure subtile autorise certains objets d'avoir un spin demi-entier. Pour de tels objets, faire un tour complet sur eux-mêmes n'est pas suffisant pour les faire revenir à leur position de départ mais il est indispensable d'effectuer une rotation d'angle 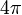 . De tels objets font partie de ce qu'on nomme le groupe double. On rencontre rarement de tels objets à notre échelle (quoiqu'on puisse donner des illustrations macroscopiques de ce comportement[1]), mais dans le monde microscopique ils sont courants. On les nomme des fermions, dont un exemple bien connu est l'électron, qui possède exactement un spin
. De tels objets font partie de ce qu'on nomme le groupe double. On rencontre rarement de tels objets à notre échelle (quoiqu'on puisse donner des illustrations macroscopiques de ce comportement[1]), mais dans le monde microscopique ils sont courants. On les nomme des fermions, dont un exemple bien connu est l'électron, qui possède exactement un spin  .
.
De façon plus rigoureuse, comme on va le voir plus bas, l'analyse du comportement des objets sous l'effet des rotations nécessite de prendre en compte la structure mathématique de groupe constitué par celles-ci. À un objet se transformant sous les rotations est alors associée une représentation de groupe. Deux objets ayant des propriétés de symétrie identiques seront par conséquent associés à des représentations équivalentes du groupe des rotations. De ce point de vue, le spin n'est rien d'autre qu'un nombre qui sert à classifier les différentes représentations inéquivalentes du groupe des rotations (on nomme cela les représentations irréductibles). C'est ainsi qu'on peut dire qu'une particule de spin 2 telle que le graviton (voir ci-dessous) possède la même symétrie du point de vue des rotations qu'une dame de pique car tous deux se transforment dans des représentations équivalentes.
Spin des particules usuelles
Le spin d'une particule est un nombre entier ou demi-entier positif, noté 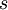 .
.
Bien que lié aux phénomènes de quantification du moment angulaire, le spin est bel et bien une propriété intrinsèque des particules. Surtout, il ne correspond à aucun mouvement de rotation hypothétique de ces particules.
Les particules possédant un spin demi-entier se nomment fermions, celles possédant un spin entier se nomment bosons. Plus particulièrement :
- Spin 0 : le boson de Higgs, particule hypothétique, non toujours découverte expérimentalement.
- Spin 1/2 : l'électron, le positron, le proton, le neutron, les neutrinos, les quarks, etc.
- Spin 1 : le photon, les bosons W± et Z0 vecteurs de l'interaction faible.
- Spin 2 : le graviton, particule hypothétique vecteur de la gravitation.
Le spin de particules composées, comme le proton, le neutron, le noyau atomique ou l'atome, est constitué des spins des particules qui les composent auxquels s'ajoute le moment angulaire des particules élémentaires l'une comparé à l'autre.
Historique
La notion de spin a été introduite par Pauli en décembre 1924[2] pour l'électron, afin d'expliquer un résultat expérimental qui restait incompréhensible dans le cadre naissant de la mécanique quantique non relativiste : l'effet Zeeman anormal. L'approche développée par Pauli consistait à introduire de façon ad-hoc le spin en ajoutant un postulat supplémentaire aux autres postulats de la mécanique quantique non relativiste (équation de Schrödinger, etc. ).
L'introduction du spin sert à comprendre aussi d'autres effets expérimentaux, comme les doublets des spectres des métaux alcalins, ou le résultat de l'expérience de Stern et Gerlach.
En 1928, Paul Dirac construisit une version quantique et relativiste de l'équation de Schrödinger, nommée actuellement équation de Dirac, qui sert à décrire les fermions de spin 1/2. Le spin y apparaît comme une propriété dérivée de son équation, et non comme un postulat supplémentaire à rajouter de façon ad-hoc.
Enfin, c'est en théorie quantique des champs que le spin montre son caractère le plus essentiel. L'analyse du groupe de Poincaré effectuée par Wigner en 1939 montra en effet qu'une particule est associée à un champ quantique, opérateur qui se transforme comme une représentation irréductible du groupe de Poincaré. Ces représentations irréductibles se classent par deux nombres réels positifs : la masse et le spin.
Le spin du photon a été découvert expérimentalement par Raman et Bhagavantam en 1931[3].
«Rotation propre»
Historiquement, le spin a en premier lieu été interprété par Uhlenbeck et Goudsmit en septembre 1925[4], [5] comme étant un moment cinétique intrinsèque, c'est-à-dire comme si la particule «tournait sur elle-même». Cette vision classique d'une «rotation propre» de la particule est en fait trop naïve ; en effet :
- si la particule est ponctuelle, la notion de rotation propre autour de son axe est tout simplement dénuée de sens physique[6].
- si la particule n'est pas ponctuelle, alors la notion possède un sens, mais on se heurte dans ce cas à une autre difficulté[7]. Supposons par exemple que la particule soit un électron, modélisé comme étant un corps sphérique de rayon a. On obtient une estimation du rayon a en écrivant que l'énergie de masse de l'électron est de l'ordre de grandeur de son énergie potentielle électrostatique, soit :
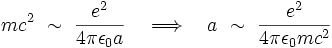 |
- La valeur numérique de ce «rayon classique» de l'électron est :
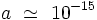 m. Si on attribue alors à cet électron un moment cinétique identique à
m. Si on attribue alors à cet électron un moment cinétique identique à 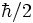 , on obtient pour un point de l'équateur une vitesse v vérifiant :
, on obtient pour un point de l'équateur une vitesse v vérifiant :
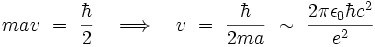 |
- La valeur numérique vaudrait :
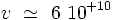 m/s, par conséquent la vitesse serait supérieure à la vitesse de la lumière dans le vide, ce qui pose des problèmes avec la théorie de la relativité restreinte.
m/s, par conséquent la vitesse serait supérieure à la vitesse de la lumière dans le vide, ce qui pose des problèmes avec la théorie de la relativité restreinte. - Ce calcul néglige les effets relativistes sur la masse[8].
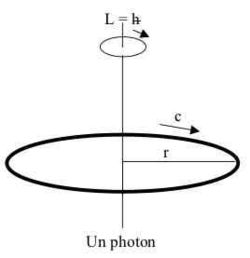
Le photon reconnu comme une petite masse m tournant à la vitesse c de la lumière à l'extrémité du rayon :
|
|
Selon la relativité, la masse en mouvement d'un photon est donnée par la relation d'Einstein-Planck E = hν = mc2. On en déduit le moment cinétique angulaire du photon
|
|
Le photon peut par conséquent être modélisé comme un anneau en rotation de masse hν / c2 en accord avec son spin un. "Il faut bien dire que ces images géométriques trop précises ne sont pas appréciées des physiciens modernes"[9]
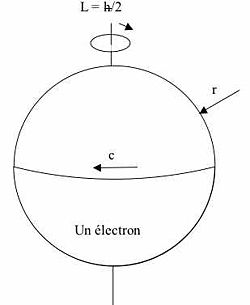
Spin de l'électron
Le calcul est plus compliqué que pour le photon car l'électron possède une masse au repos non nulle. MacGregor, dans son ouvrage, The Enigmatic Electron[10], montre qu'il faut tenir compte de la variation relativiste de la masse avec la vitesse de rotation. Il fait l'hypothèse que la vitesse équatoriale de l'électron au repos est identique à la vitesse c de la lumière. Calculons la masse m observée d'une sphère pleine (une boule) de rayon R en rotation relativiste à la vitesse v = ωr. La vitesse de rotation angulaire est supposée constante, c'est-à-dire que l'électron est un solide rigide, de résistance mécanique illimitée et non un fluide. Soit ρ (r) la masse spécifique à la distance r de l'axe de rotation et ρ0 sur l'axe de rotation où la matière est au repos. Le volume étant inchangé, la masse spécifique relativiste est :
|
|
La hauteur du cylindre élémentaire est h. La vitesse linéaire de rotation, v = ωr, est identique à c sur l'équateur, ce qui donne la vitesse angulaire ω = c / R. On a par conséquent, en tenant compte de la variation relativiste de la masse :
|
|
On calcule de même le moment d'inertie relativiste de la sphère pleine (boule), assez peu différent du moment classique 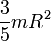 :
:
|
|
La simplification est principale dans ce calcul, quasiment inextricable dans le cas général. La relation d'Einstein-Planck donne la fréquence propre ν de l'électron. En l'identifiant à sa vitesse de rotation angulaire ω, on a :
|
|
On obtient pour l'électron un rayon différent du rayon "classique"
|
|
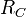 est le rayon de Compton, celui-là même qui apparaît dans l'équation de Klein-Gordon et , évidemment, dans l'effet Compton. MacGregor obtient ainsi le moment cinétique intrinsèque de l'électron :
est le rayon de Compton, celui-là même qui apparaît dans l'équation de Klein-Gordon et , évidemment, dans l'effet Compton. MacGregor obtient ainsi le moment cinétique intrinsèque de l'électron :
|
|
en accord avec l'observation. Cela donne un spin de 1/2 en unités de 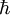 . Le cœfficient 1/2 du moment cinétique de l'électron s'explique par le moment d'inertie relativiste où le cœfficient 3/5 est remplacé par 1/2 pour une vitesse périphérique identique à la vitesse de la lumière.
. Le cœfficient 1/2 du moment cinétique de l'électron s'explique par le moment d'inertie relativiste où le cœfficient 3/5 est remplacé par 1/2 pour une vitesse périphérique identique à la vitesse de la lumière.
Ce calcul a été fait pour un électron en rotation mais avec son axe au repos. Il serait à revoir pour un électron en mouvement quelconque relativiste. Le modèle de la toupie pour le spin de l'électron semble en accord à la fois avec les théories relativiste et quantique. La difficulté signalée au paragraphe précédent est résolue en tenant compte de la variation relativiste de la masse en rotation et en assimilant la vibration de l'électron à une rotation.
Il reste cependant à mesurer directement le rayon toujours inconnu de cette particule élémentaire néenmoins connue depuis un siècle. On considère aujourd'hui que son rayon est nul ce qui exigerait que sa masse le soit aussi.
Mais ce problème ne se pose plus avec la vision moderne du spin, qui affirme qu'une particule élémentaire n'a pas de taille, que le spin est un objet purement quantique, que l'usage du mot spin est historique et que le modèle de la toupie est dépassé, remplacé par celui de Dirac.
Comme on vient de le voir, chez le photon comme chez l'électron, l'équateur, dont le rayon est celui de Compton, est en rotation à la vitesse de la lumière. Le photon et l'électron peuvent être modélisés respectivement par un anneau et par une sphère pleine (boule). Ce calcul reste cependant limité (pour le moment ?) à un photon de vitesse c constante ainsi qu'à un électron à faible vitesse de translation.
Opérateur spin
En mécanique quantique, le spin est un opérateur vectoriel hermitien comportant trois composantes, notées habituellement 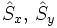 et
et 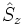 par référence aux trois axes de coordonnées cartésiennes de l'espace physique. Ces composantes vérifient les relations de commutations :
par référence aux trois axes de coordonnées cartésiennes de l'espace physique. Ces composantes vérifient les relations de commutations :
où εijk est le symbole de Levi-Civita. Ces relations de commutations sont analogues à celles découvertes en novembre 1925 par Born, Heisenberg et Jordan pour les composantes du moment cinétique orbital : ![\left[ \, \hat{L}_i \, , \ \hat{L}_j \, \right] \ = \ i \ \hbar \ \epsilon_{ijk} \ \hat{L}_k](illustrations/50b2055de1bf66ce973994caf003e045.png)
Par ressemblance avec les résultats obtenus pour l'instant cinétique orbital (ou d'une façon plus générale pour un moment cinétique quantique), il existe pour l'opérateur spin une base de vecteurs propres notés | s, ms >, où s est entier ou demi-entier, et ms est un entier ou demi-entier prenant l'une des 2s + 1 valeurs 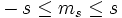 , tels que :
, tels que :
Spin 1/2 - matrices de Pauli
Pour une particule de spin 1/2 comme l'électron, on a s = 1 / 2, par conséquent 2s + 1 = 2 : il existe uniquement deux états de spin différents, caractérisés par 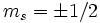 .
.
On note fréquemment les deux états propres correspondant : 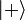 et
et 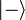 , ou encore symboliquement :
, ou encore symboliquement : 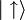 et
et 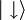 .
.
Pauli a introduit trois matrices 2 x 2, notées 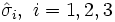 telles que l'opérateur de spin s'écrive :
telles que l'opérateur de spin s'écrive :
Ces trois matrices de Pauli s'écrivent explicitement :
Elles satisfont les relations de commutation :
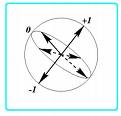
Représentation géométrique du spin par une sphère de Riemann
Un état quantique quelconque d'une particule de spin 1/2 peut s'exprimer sous la forme générale :
(a et b étant deux nombres complexes). Cette formule exprime une superposition des deux états propres.
Selon les règles de la mécanique quantique, l'état quantique représenté par 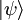 et
et 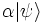 sont physiquement rigoureusement les mêmes. Donc, on peut aussi exprimer l'état général d'une particule de spin 1/2 par :
sont physiquement rigoureusement les mêmes. Donc, on peut aussi exprimer l'état général d'une particule de spin 1/2 par :
L'état de spin 1/2 est par conséquent entièrement caractérisé par un nombre complexe 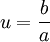 . Ce rapport pouvant être illimité lorsque a = 0 (état pur de spin "down"), il est indispensable d'utiliser une sphère de Riemann pour représenter ce rapport, la sphère de Riemann étant une extension du corps des complexes avec l'infini.
. Ce rapport pouvant être illimité lorsque a = 0 (état pur de spin "down"), il est indispensable d'utiliser une sphère de Riemann pour représenter ce rapport, la sphère de Riemann étant une extension du corps des complexes avec l'infini.
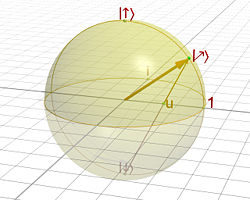
Selon cette représentation, tout état de spin 1/2 trouve une représentation géométrique (voir figure ci-contre). Le vecteur passant par l'origine et pointant sur la projection du complexe u sur la sphère de Riemann donne une visualisation géométrique de l'état de spin 1/2 comme étant une direction dans l'espace.
Bien que semblant a priori purement mathématique, cette représentation de l'état de spin comme étant une direction dans l'espace possède une certaine pertinence. Surtout, on peut retrouver simplement avec cette représentation géométrique la probabilité d'obtenir l'état 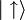 et
et 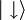 lors d'une mesure de l'état
lors d'une mesure de l'état 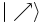 (il ne faut pas perdre de vue que l'état mesuré d'un état de spin 1/2 sera toujours soit
(il ne faut pas perdre de vue que l'état mesuré d'un état de spin 1/2 sera toujours soit 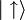 soit
soit 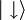 ).
).
Moment magnétique de spin
Définition. Facteur de Landé
Au moment cinétique orbital d'une particule de charge q et de masse m est associé un moment magnétique orbital :
Le facteur q / 2m est nommé rapport gyromagnétique. De même, on associe à une particule de charge q, de masse m, et de spin donné un moment magnétique de spin :
où g est un nombre sans dimension, nommé facteur de Landé (1921). Ce nombre fluctue selon la nature de la particule : on a approximativement g = 2 pour l'électron, g = 5, 586 pour le proton, et 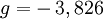 pour le neutron[11]. On trouve aussi des valeurs moitié pour le proton et le neutron qui correspondraient à un moment magnétique anormal.
pour le neutron[11]. On trouve aussi des valeurs moitié pour le proton et le neutron qui correspondraient à un moment magnétique anormal.
Magnéton de Bohr
Pour l'électron, on a les valeurs suivantes : 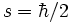 et g = 2, 002 ; on introduit alors le «quantum magnétique» suivant, nommé magnéton de Bohr :
et g = 2, 002 ; on introduit alors le «quantum magnétique» suivant, nommé magnéton de Bohr :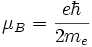
Moment magnétique anormal de l'électron
L'équation de Dirac prédit pour l'électron un facteur de Landé précisément identique à : g = 2. Or, la valeur expérimentale admise en 2005 vaut :
Il existe par conséquent un écart, décelé pour la première fois en 1947 dans la structure hyperfine de l'hydrogène et du deutérium[12] : on parle alors du moment magnétique anormal de l'électron. La théorie quantique des champs du modèle standard sert à rendre compte de cette anomalie avec une très grande précision.
Spin et dynamique géométrique
A considérer que la dynamique soit un corollaire de la géométrie d'espace-temps, l'évolution d'une particule dans l'espace-temps serait décrite comme une chaîne d'objets géométriques reliés. Dans ce cas, la géométrie de l'espace-temps est déterminée seulement par la fonction sigma d'un espace de Minkowski et la chaîne hélicoïdale de cet l'espace-temps définirait alors la rotation des particules à une vitesse supraluminique [1].
Notes et références
- ↑ Voir par exemple ici ce petit jeu mathématique
- ↑ Wolfgang Pauli ; Zeitschrift fur Physik 31 (1925) 373
- ↑ Indian J. Phys. 6 353-366 (1931)
- ↑ Un problème de facteur 2 dans la structure fine du spectre de l'hydrogène, identifié par Heisenberg, fut résolu en décembre 1925 avec l'aide d'Einstein, sous l'impulsion de Bohr. Ce dernier demanda à deux physiciens hollandais de publier le résultat en urgence : S. Goudsmit et G. E. Uhlenbeck ; Nature 117 (1926) 264.
- ↑ George E. Uhlenbeck et Samuel Goudsmit ; Naturwissenschaften 13 (1925) 953
- ↑ Par définition, l'axe de rotation d'un objet est le lieu de points de cet objet qui restent immobiles. Si la particule est ponctuelle, son axe propre est sur la particule, par conséquent celle-ci est immobile.
- ↑ Il faudrait aussi expliquer quelles sont les forces internes qui assurent la cohésion de cet électron étendu. Ce problème a occupé la plupart de théoriciens dans les années 1895 à 1930, avant que l'électrodynamique quantique et son électron ponctuel ne deviennent bien établies.
- ↑ Ce qui tempère la valeur de cet argument, qui reste néenmoins particulièrement utilisé, l'opinion le plus souvent répandue étant que cette simplification ne change pas la conclusion. Cependant, il existe d'autres tentatives de prise en compte de la masse relativiste (voir par exemple Mass and Spin Renormalization in Lorentz Electrodynamics Article disponible sur arXiv : math-ph/0009003. (en) ) Il faut aussi rappeler la théorie de Dirac qui est aussi relativiste, mais purement mathématique.
- ↑ Rocard, Y, Thermodynamique, Masson, 1957, p. 250
- ↑ MacGregor M. H., The Enigmatic Electron, Kluwer, Dordrecht, 1992
- ↑ Quoique le neutron ait une charge q = 0, on lui attribue ici un facteur de Landé correspondant au moment magnétique de spin calculé pour la valeur q = e, pour le comparer à ceux de l'électron et du proton.
- ↑ Marc Knecht ; The anomalous magnetic moments of the electron and the muon, séminaire Poincaré (Paris, 12 octobre 2002) [pdf][lire en ligne], publié dans : Bertrand Duplantier et Vincent Rivasseau (Eds. ) ; Poincaré Seminar 2002, Progress in Mathematical Physics 30, Birkhäuser (2003), ISBN 3-7643-0579-7.
- Wolfgang Pauli ; Zeitschrift fur Physik 31 (1925) 373.
- George E. Uhlenbeck et Samuel Goudsmit ; Naturwissenschaften 13 (1925) 953.
- Samuel Goudsmit et George E. Uhlenbeck ; Nature 117 (1926) 264.
- Sin-Itiro Tomonaga ; The story of spin, The university of Chicago press (1997), ISBN 0-226-80794-0. Traduction anglaise d'un ouvrage paru en japonais en 1974.
- Marc Knecht ; The anomalous magnetic moments of the electron and the muon, séminaire Poincaré (Paris, 12 octobre 2002), publié dans : Bertrand Duplantier et Vincent Rivasseau (Eds. ) ; Poincaré Seminar 2002, Progress in Mathematical Physics 30, Birkhäuser (2003), ISBN 3-7643-0579-7.
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

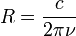
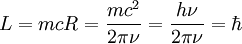
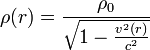
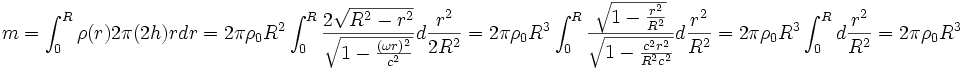
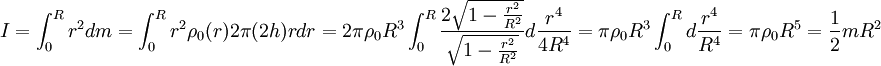
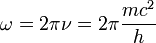
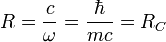
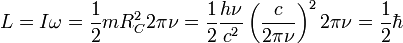
![\left[ \, \hat{S}_i \, , \ \hat{S}_j \, \right] \ = \ i \ \hbar \ \epsilon_{ijk} \ \hat{S}_k](illustrations/56736a4c37a2470ddb3bc4bf03c15bab.png)
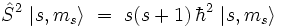
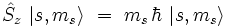
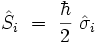
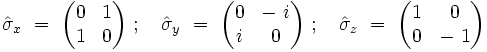
![\left[ \, \hat{\sigma}_i \, , \ \hat{\sigma}_j \, \right] \ = \ 2 \ i \ \epsilon_{ijk} \ \hat{\sigma}_k](illustrations/f0e84d8251c96b1f008b317be9a55e54.png)
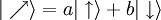
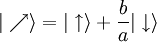
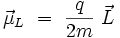
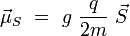
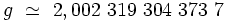

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité