Formulaire de physique quantique
Les relations de commutation entre les observables se déduisent du principe de correspondance entre la mécanique hamiltonienne et la mécanique quantique.
Recherche sur Google Images :
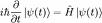
Source image : fr.wikipedia.org Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- Premier semestre d'un cours de mécanique quantique dispensé en licence de physique à l'universite... Principe de moindre action et équation de Lagrange Équations de Hamilton... Formule de Weizsäcker et le modèle de la goutte liquide... Description de l'évolution dans le temps. La description de Schrödinger... (source : librecours)
|
formulaire de physique |
| Optique |
| Électro- Magnéstatique |
| Physique quantique |
| Thermodynamique |
| Mécanique des fluides |
| Mécanique |
| Relativité restreinte |
| Trou noir |
| Analyse vectorielle |
Expression de quelques observables
Les relations de commutation entre les observables se déduisent du principe de correspondance entre la mécanique hamiltonienne et la mécanique quantique. Leurs expressions peuvent alors être trouvées à partir d'une analyse mathématique.
| Observable | Symbole | Expression (s) | Commentaire |
|---|---|---|---|
| Position | 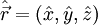 |
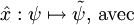
|
|
| impulsion | 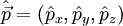 |
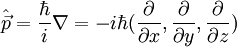
|
La seconde formule est valable pour une particule chargée en jauge de coulomb |
| Énergie cinétique | 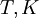 |
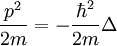 |
|
| Moment cinétique orbital | 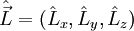 |
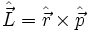
|
Les vecteurs propres communs à L2 ainsi qu'à Lz forment les harmoniques sphériques |
| Spin | 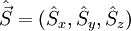 |
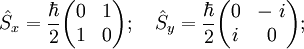
|
Formules valables dans le cas d'un spin 1/2 |
| Moment cinétique total | 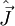 |
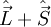 |
|
| Carré du moment cinétique | 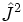 |
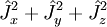 |
|
| Champ électrique | 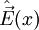 |
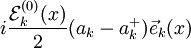 |
Valable pour un seul mode (k) du champ. 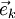 est le vecteur unitaire indiquant la polarisation. est le vecteur unitaire indiquant la polarisation. |
- Pour un état quelconque : l'état évolue selon l'équation de Schrödinger dépendant du temps
- Pour un état propre de l'énergie, c'est-à-dire répondant à l'équation aux valeurs propres
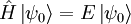 à l'instant d'origine t=0, l'évolution aux instants ultérieurs (t>0) sera :
à l'instant d'origine t=0, l'évolution aux instants ultérieurs (t>0) sera : 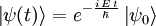
Expression de quelques hamiltoniens
| Nom | Expression | Commentaire |
|---|---|---|
| Particule dans un potentiel | 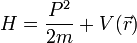 |
V (r) si potentiel central (ie à symétrie sphérique) |
| Potentiel coulombien | 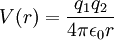 |
|
| Potentiel harmonique | 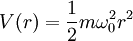 |
|
| Puits carré avec barrières illimitées | ![V(r)=0 \text{ si } L\in[-L/2, L/2]](illustrations/dd3e008b6d8167adfc881f63be936425.png)
|
La condition 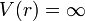 est équivalente à ψ (r) = 0. est équivalente à ψ (r) = 0. |
| Interaction simplifiée entre deux moments cinétiques | 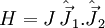 |
|
| Couplage dipolaire électrique, approche semiclassique | 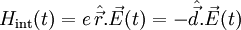 |
E (t) est le champ électrique à l'endroit où se trouve le dipôle. d est le moment dipolaire électrique. |
| Hamiltonien d'un mode du champ électromagnétique | 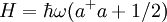 |
Le hamiltonien d'un oscillateur harmonique 1D peut être mis sous la même forme. |
| Hamiltonien de Jaynes-Cummings (atome à deux niveaux interagissant avec un mode unique du champ avec les approximations dipolaire électrique et du champ tournant) | 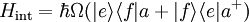 |
|
Propagateur de l'équation de Schrödinger
À partir de la notion d'exponentielle de matrice, on peut trouver la solution formelle de l'équation de Schrödinger. Cette solution s'écrit :
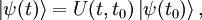 avec
avec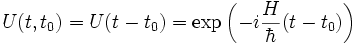 dans le cas où H ne dépend pas explicitement du temps, et
dans le cas où H ne dépend pas explicitement du temps, et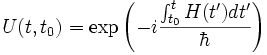 dans le cas général.
dans le cas général.
| Représentation : | |||
| Heisenberg | Interaction | Schrödinger | |
| Ket | constant | 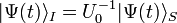 |
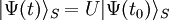 |
| Observable | AH (t) = U − 1ASU | 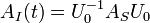 |
constant |
| Opérateur d'évolution | 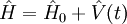 |
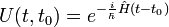 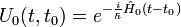 |
|
| Mécanique quantique : Théorème d'Ehrenfest • Équation de Schrödinger • Propagateur | |||
Représentation de Heisenberg
Si le hamiltonien ne dépend pas explicitement du temps, dans la représentation respectant les traditions nommée représentation de Schrödinger, les observables ne dépendent pas du temps et l'état dépend du temps. Par une transformation unitaire, on peut passer à la représentation de Heisenberg, où l'état est indépendant du temps et les observables dépendent du temps suivant l'équation ci-dessous :
Loi du corps noir
D'après la loi de Stefan-Boltzmann, le flux d'énergie Φ émis par le corps noir fluctue selon la température absolue T (en kelvin) selon
- Φ = σT4
où σ est la constante de Stefan-Boltzmann
La densité de flux d'énergie dΦ pour une longueur d'onde λ donnée est donné par la loi de Planck :
où c est la vitesse de la lumière dans le vide, h est la constante de Planck et k est la constante de Boltzmann. Le maximum de ce spectre est donné par la loi de Wien :
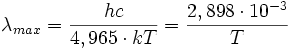 .
.
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

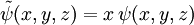
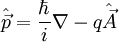
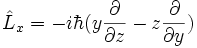
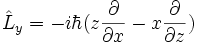
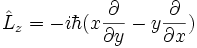
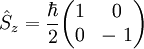
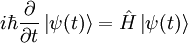
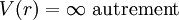
![{d \over {dt}}A={1 \over {i\hbar}}[A,H]+\left({{\partial A} \over {\partial t}}\right)_\text{explicite}](illustrations/d78888ebea89231f9ded80d03d9445c6.png)
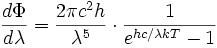

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité