Interaction d'échange
En physique, l'interaction d'échange est un effet quantique qui accroît ou décroît l'énergie d'un ou plusieurs électrons quand leurs fonctions d'ondes se superposent.
Recherche sur Google Images :
Source image : iramis.cea.fr Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- L'interaction d'échange est un couplage de spin propre à l'exciton.... Symétrie ; Structure bande ; Exciton ; Interaction électron spin ;... (source : books.google)
- La présence d'électrons libres fait de ces molécules des entités électroactives..... En effet, dans le cas du ligand libre, seule une interaction spin – spin... (source : cat.inist)
En physique, l'interaction d'échange est un effet quantique qui accroît ou décroît l'énergie d'un ou plusieurs électrons quand leurs fonctions d'ondes se superposent. Conséquence du principe d'exclusion de Pauli, cette modification d'énergie est le résultat de l'identité des particules, de la symétrie d'échange et de la force électrostatique. Les effets de l'interaction d'échange furent découverts de manière indépendantes par Heisenberg[1] et Dirac[2] en 1926.
L'interaction d'échange est aussi nommée force d'interaction[3], mais est à distinguer des forces d'échange produites par l'échange de porteurs de forces, comme la force électromagnétique produite entre deux électrons par l'échange d'un photon, ou la force forte entre deux quarks produite par l'échange d'un gluon[4].
Aperçu
Les particules quantiques sont classées soit comme bosons, soit comme fermions. Le théorème spin-statistique de la théorie quantique des champs stipule que l'ensemble des particules à spin demi-entier se comportent comme des fermions et l'ensemble des particules à spin entier se comportent comme des bosons. Plusieurs bosons peuvent occuper le même état quantique ; cependant, en raison du principe d'exclusion de Pauli, deux fermions ne peuvent occuper le même état quantique simultanément. Les électrons ayant un spin demi-entier, ils sont des fermions. Ceci veut dire que la fonction d'onde globale d'un dispositif doit être antisymétrique quand deux électrons sont échangés.
Si on considère un dispositif à deux électrons, on peut essayer de modéliser l'état de chaque électron en postulant dans un premier temps l'indépendance de leur comportement, et en considérant leurs fonctions d'ondes respectives dans l'espace en Ψ1 (r1) pour le premier électron et en Ψ2 (r2) pour le second. On suppose que Ψ1 et Ψ2 sont orthogonales, et que chacune correspond à une valeur propre de l'énergie pour son électron. Si désormais le dispositif complet est de spin total 1, la partie de la fonction d'onde associée au spin est symétrique, et la partie spatiale de la fonction d'onde du dispositif doit être antisymétrique pour obtenir une fonction d'onde globale antisymétrique. Ceci peut être obtenu en antisymétrisant le produit des fonctions d'ondes spatiales pour la position spatiale reconnue :
Pour un dispositif dans un état de spin nul, la fonction d'onde de spin est antisymétrique et la partie spatiale de la fonction d'onde globale doit être symétrique :
Si on suppose que l'énergie d'interaction entre les deux électrons, VI (r1, r2) , est symétrique comparé à l'échange des 2 électrons, et qu'on se restreint à l'espace vectoriel balayé par ΨA et ΨS, alors chacune de ces fonctions d'ondes donnera des valeurs propres pour l'énergie du dispositif, et les différences entre leurs énergies sera :
Si on prend en compte les différents spins reliés à ces valeurs propres, on peut modéliser cette différence en ajoutant un terme d'interaction spin-spin :
au hamiltonien, où S1 et S2 sont les opérateurs de spin des deux électrons. Ce terme, quelquefois nommé hamiltonien d'Heisenberg, donne une forme de l'interaction d'échange[5], [6], [7]. Malgré sa forme, il n'est pas de nature magnétique. Dans des matériaux comme le fer, cet effet facilite les électrons à spins parallèles et est par conséquent une cause de ferromagnétisme[8].
Voir aussi
- symétrie d'échange
- principe d'exclusion de Pauli
- déterminant de Slater
Références et notes
- ↑ W. Heisenberg, Mehrkörperproblem und Resonanz in der Quantenmechanik, Zeitschrift für Physik 38, #6–7 (Juin 1926), p. 411–426. DOI 10.1007/BF01397160.
- ↑ P. A. M. Dirac, On the Theory of Quantum Mechanics, Proceedings of the Royal Society of London, Series A 112, #762 (1er octobre 1926), p. 661–677.
- ↑ James D. Livingston, Driving Force : the natural magic of magnets, Harvard University Press, 1996, p. 87–88. ISBN 0674216458.
- ↑ (en) Exchange Forces, HyperPhysics, Université d'État de Géorgie, vérifié le 2 juin 2007.
- ↑ (en) Derivation of the Heisenberg Hamiltonian, Rebecca Hihinashvili, consulté en ligne le 2 octobre 2007.
- ↑ Quantum Theory of Magnetism : Magnetic Properties of Materials, Robert M. White, 3rd rev. ed., Berlin : Springer-Verlag, 2007, section 2.2.7. ISBN 3-540-65116-0.
- ↑ The Theory of Electric and Magnetic Susceptibilities, J. H. van Vleck, London : Oxford University Press, 1932, chapitre XII, section 76.
- ↑ Exchange interaction, F. Duncan and M. Haldane, AccessScience@McGraw-Hill, DOI 10.1036/1097-8542.247650, daté du 10 avril 2000.
Liens externes
- (en) Exchange Interaction (PDF)
- (en) Exchange Interaction and Energy
- (en) Exchange Interaction and Exchange Anisotropy
- (en) Cet article est partiellement ou en totalité issu d'une traduction de l'article de Wikipédia en anglais intitulé «Exchange interaction».
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

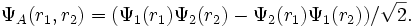
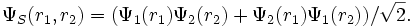
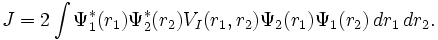
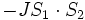

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité