Statistique de Fermi-Dirac
En mécanique quantique et en physique statistique, la statistique de Fermi-Dirac sert à désigner la distribution statistique de fermions indiscernables sur les états d'énergie d'un dispositif à l'équilibre thermodynamique.
Recherche sur Google Images :
Source image : fr.wikipedia.org Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- du gaz classique, que l'effet de la statistique de Fermi-Dirac est de diminuer la chaleur specifique par un facteuregal `a (π... (source : books.google)
- La statistique de Fermi-Dirac est appliquée pour décrire la probabilité d'occupation des différents sites interstitiels. Deux cas limites sont traités :... (source : cat.inist)
En mécanique quantique et en physique statistique, la statistique de Fermi-Dirac sert à désigner la distribution statistique de fermions indiscernables (tous identiques) sur les états d'énergie d'un dispositif à l'équilibre thermodynamique. La distribution en question tient à une particularité des fermions : les particules de spin demi-entier sont assujetties au principe d'exclusion de Pauli, à savoir que deux particules ne peuvent occuper simultanément un même état quantique.
Note historique : un problème de statistique
Avant l'avènement de la distribution de Fermi-Dirac dans les années 1920, notre compréhension du comportement des électrons dans les métaux était quelque peu rudimentaire. Ainsi on ne comprenait pas particulièrement bien pourquoi les électrons participent en grand nombre dans la conduction du courant électrique dans un métal et que ce nombre devenait extrêmement réduit lorsqu'il s'agit de contribuer à la capacité calorifique du même métal. Il y a manifestement ici un problème de statistique qui se pose dans l'évaluation de la capacité calorifique des métaux. L'explication fut apportée exactement par la distribution de Fermi-Dirac qui révéla que seuls les états localisés près du niveau de Fermi, étaient sollicités pour la contribution à la capacité calorifique du métal.
Statistique de Fermi-Dirac
La statistique de Fermi-Dirac a été introduite en 1926 par Enrico Fermi et Paul Dirac. En 1927 elle fut appliquée aux électrons dans un métal par Arnold Sommerfeld. Statistiquement, le nombre ni de particules dans l'état d'énergie Ei est donné par
où :
- gi est la dégénérescence de l'état d'énergie Ei, à savoir le nombre d'états possédant cette énergie ;
- μ est le potentiel chimique ;
- kB est la constante de Boltzmann ;
- T est la température absolue.
Utilisation de cette distribution
Les distributions de Bose-Einstein et de Fermi-Dirac sont utilisées quand les effets quantiques sont pris en compte, et quand les particules sont reconnues comme indiscernables. Cela correspond à une concentration de particules (N/V) supérieur à une certaine densité d'état, autrement dit que la distance intermoléculaire est inférieur à celle de la longueur d'onde thermique de de Broglie. Les fonctions d'onde peuvent "se toucher" mais pas se superposer.
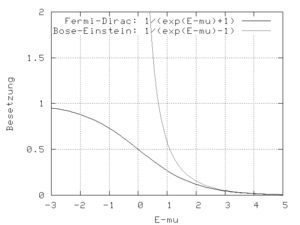
Limite classique et comparaison avec les bosons
À haute température, quand les effets quantiques ne se font plus sentir, la statistique de Fermi-Dirac tend vers la statistique de Maxwell-Boltzmann; il en est de même pour la statistique de Bose-Einstein qui régit les bosons. À basse température, si les particules occupent en priorité les niveaux d'énergie les plus faibles, les statistiques changent cependant. A titre d'exemple, à température nulle :
- avec la statistique de Fermi-Dirac, le niveau qui plus est basse énergie, E0, est occupé par au plus g0 fermions; les états de basse énergie Ei sont ensuite occupés chacun dans l'ordre croissant des énergies par au plus gi fermions jusqu'à épuisement de ces derniers;
- avec la statistique de Bose-Einstein, le niveau qui plus est basse énergie contient l'ensemble des bosons (cas limite du condensat de Bose-Einstein).
Gaz de fermions quantiques
Les électrons dans les solides forment un gaz de fermions dont la description requiert la statistique de Fermi-Dirac. Il y a peu de temps, le refroidissement de gaz d'atomes dilués fermioniques jusqu'à des températures de l'ordre du μK a permis d'obtenir des gaz de fermions dégénérés, seulement descriptibles par cette statistique.
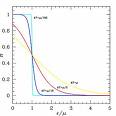
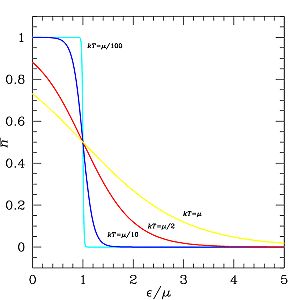
Effet de la température sur la distribution de Fermi-Dirac
En bas de page de ce cours, une application interactive animée, rédigée en langage java, montre l'effet de la température T sur la distribution de Fermi-Dirac. On y voit surtout pourquoi seuls les états près du niveau de Fermi sont sollicités lors de la conduction.
Références
- Charles Kittel (trad. Nathalie Bardou, Évelyne Kolb), Physique de l'état solide (Solid state physics), 1998 [détail des éditions]
Voir aussi
- Autres distributions statistiques en mécanique quantique
- en mécanique quantique : statistique de Bose-Einstein
- en mécanique classique : statistique de Maxwell-Boltzmann
- physique statistique
- physique quantique
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

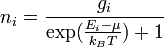

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité