Statistique de Bose-Einstein
En mécanique quantique et en physique statistique, la statistique de Bose-Einstein sert à désigner la distribution statistique de bosons indiscernables sur les états d'énergie d'un dispositif à l'équilibre thermodynamique.
Recherche sur Google Images :

Source image : fr.wikiversity.org Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- Bose - Einstein, statistique de , approche statistique quantique, développée par le physicien indien Satyendranath Bose en collaboration avec... (source : fr.wikiversity)
- Répartition statistique de Bose - Einstein 3. Répartition statistique de Fermi -... Limite commune des statistiques de Bose - Einstein et Fermi - Dirac... (source : sciences.univ-nantes)
En mécanique quantique et en physique statistique, la statistique de Bose-Einstein sert à désigner la distribution statistique de bosons indiscernables (tous identiques) sur les états d'énergie d'un dispositif à l'équilibre thermodynamique. La distribution en question résulte d'une particularité des bosons : les particules de spin entier ne sont pas assujetties au principe d'exclusion de Pauli, à savoir que plusieurs bosons peuvent occuper simultanément un même état quantique.
Distribution de Bose-Einstein
La statistique de Bose-Einstein a été introduite par Satyendranath Bose en 1920 pour les photons et généralisée aux atomes par Albert Einstein en 1924. Statistiquement, à l'équilibre thermodynamique, le nombre ni de particules dans l'état d'énergie Ei est
où :
- gi est la dégénérescence de l'état d'énergie Ei, à savoir le nombre d'états possédant cette énergie ;
- μ est le potentiel chimique ;
- kB est la constante de Boltzmann ;
- T est la température.
Limite classique et comparaison avec les fermions
À haute température, quand les effets quantiques ne se font plus sentir, la statistique de Bose-Einstein, comme la statistique de Fermi-Dirac qui régit les fermions, tend vers la statistique de Maxwell-Boltzmann. Aux basses températures, cependant, les deux statistiques changent entre elles. Ainsi, à température nulle :
- avec la statistique de Bose-Einstein, le niveau qui plus est basse énergie contient l'ensemble des bosons;
- avec la statistique de Fermi-Dirac, les niveaux qui plus est basse énergie contiennent chacun au plus gi fermions.
Condensat de Bose-Einstein
Comme vu auparavant, la statistique de Bose-Einstein prévoit qu'à température nulle, l'ensemble des particules occupent le même état quantique, celui qui plus est basse énergie. Ce phénomène est observable à l'échelle macroscopique et forme un condensat de Bose-Einstein.
Voir aussi
- Autres distributions statistiques en mécanique quantique
- en mécanique quantique : statistique de Fermi-Dirac
- en mécanique classique : statistique de Maxwell-Boltzmann
- physique statistique
- physique quantique
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

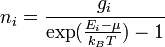

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité