Approximation orbitale
Un dispositif chimique est constitué de noyaux et d'électrons. Dans le cadre de l'approximation de Born-Oppenheimer, les électrons sont décrits collectivement par une fonction d'onde dite multiélectronique.
Recherche sur Google Images :
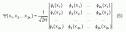
Source image : www.unige.ch Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- ... Ainsi, les orbitales atomiques sont des fonctions qui donnent la... étant énormément plus massif que les électrons ;; l'approximation orbitale, ... (source : fr.wikiversity)
- Les fonctions d'ondes monoélectroniques décrivant les états stationnaires des électrons sont nommées orbitales. Dans un atome, on parle d'orbitale atomique... (source : books.google)
Définition
Un dispositif chimique (molécules, ions... ) est constitué de noyaux et d'électrons. Dans le cadre de l'approximation de Born-Oppenheimer, les électrons sont décrits collectivement par une fonction d'onde dite multiélectronique  . Cette fonction d'onde décrit la probabilité de trouver simultanément l'électron 1 à la position r1 et l'électron 2 à la position r2, etc. Ceci a pour conséquence que la probabilité de trouver l'électron 1 à un lieu donné dépend de la position de l'électron 2 : on dit que les électrons sont corrélés.
. Cette fonction d'onde décrit la probabilité de trouver simultanément l'électron 1 à la position r1 et l'électron 2 à la position r2, etc. Ceci a pour conséquence que la probabilité de trouver l'électron 1 à un lieu donné dépend de la position de l'électron 2 : on dit que les électrons sont corrélés.
La fonction d'onde 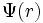 satisfait l'équation de Schrödinger :
satisfait l'équation de Schrödinger :
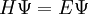
H est un opérateur nommé hamiltonien, 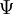 est la fonction d'onde et E est l'état énergétique associé à cette fonction d'onde. La fonction d'onde
est la fonction d'onde et E est l'état énergétique associé à cette fonction d'onde. La fonction d'onde 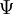 peut être décrite soit avec les coordonnées cartésiennes x, y et z, soit avec les coordonnées sphériques r,
peut être décrite soit avec les coordonnées cartésiennes x, y et z, soit avec les coordonnées sphériques r, 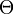 et
et 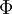 :
:
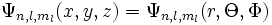
Les indices n, l et m sont les trois nombres quantiques décrivant les orbitales atomiques de l'électron :
- n est le nombre quantique principal.
![n\in[0;\infty]\,](illustrations/c7321774a22834a4efec761445afb6ac.png)
- l est le nombre quantique secondaire (ou azimuthal).
- m est le nombre quantique tertiaire (ou magnétique).
L'approximation orbitale consiste à supposer que les électrons sont quasiments indépendants les uns des autres, ce qui sert à simplifier l'écriture de la fonction d'onde : 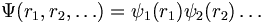
Mais cette approximation n'est pas satisfaisante car il existe des interactions entre le noyau chargé positivement et les électrons ainsi qu'entre les électrons eux-mêmes. Pour s'approcher des valeurs établies expérimentalement on utilise les règles de Slater qui permettent de moyenner pour chaque électron la charge effective : c'est le deuxième niveau d'approximation.
Chacune des fonctions d'onde 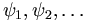 décrit un seul électron : ce sont des fonctions d'onde monoélectroniques. Les fonctions d'ondes monoélectroniques décrivant les états stationnaires des électrons sont nommées orbitales. Dans un atome, on parle d'orbitale atomique, et , quand les orbitales atomiques de plusieurs atomes interagissent, d'orbitale moléculaire.
décrit un seul électron : ce sont des fonctions d'onde monoélectroniques. Les fonctions d'ondes monoélectroniques décrivant les états stationnaires des électrons sont nommées orbitales. Dans un atome, on parle d'orbitale atomique, et , quand les orbitales atomiques de plusieurs atomes interagissent, d'orbitale moléculaire.
Principe d'exclusion de Pauli
- Dans un atome, 2 électrons ne peuvent pas avoir leurs 4 nombres quantiques semblables (n, l, m, s)
- 2 électrons dans une même orbitale atomique doivent différer par leur nombre quantique de spin = +/- 1/2
- Une orbitale atomique ne peut contenir au maximum que 2 électrons, de spins opposés, dits "antiparallèles" ou "appariés".
- S'il n'y a qu'un seul électron dans l'orbitale atomique, on le dit "célibataire" ou "non-apparié"
- Une orbitale atomique vide veut dire une "lacune électronique"
Principe de stabilité
A l'état essentiel, l'atome est dans un état énergétique le plus stable, autrement dit l'énergie la plus basse.
Règle de Hund
Aussi dit "règle du spin maximal" : Lorsque plusieurs orbitales atomiques sont de même énergie, (p, d, ... ), les électrons se répartissent avec un maximum de spins parallèles.
Voir aussi la regle de Klechkowski
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 12/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.


 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité