Corrélation électronique

L'expression de corrélation électronique est utilisée pour décrire l'interaction entre électrons dans un dispositif quantique, dont on considère la structure électronique. Le terme de corrélation provient des mathématiques statistiques et indique que deux fonctions de distribution, f et g, ne sont pas indépendantes l'une de l'autre.

Dispositifs atomiques et moléculaires

Dans la méthode de Hartree-Fock en chimie quantique, la fonction d'onde antisymétrique est approximée par un seul déterminant de Slater. Les fonctions d'ondes exactes, cependant, ne peuvent le plus souvent pas être exprimées comme déterminants simples. L'approximation d'un déterminant simple ne prend pas en compte la corrélation de Coulomb, ce qui conduit à une énergie électronique totale différente de la solution exacte de l'équation de Schrödinger non relativiste dans l'approximation de Born-Oppenheimer. Donc, la limite Hartree-Fock est toujours au-dessus de cette énergie exacte. La différence est nommée énergie de corrélation, terme forgé par Löwdin.
Une certaine partie de la corrélation électronique est déjà reconnue dans l'approximation Hartree-Fock, plus exactement dans le terme d'échange électronique décrivant la corrélation entre électrons avec des spins parallèles. La corrélation de base empêche deux électrons à spin parallèle de se trouver au même point de l'espace (selon le principe d'exclusion de Pauli), et est quelquefois nommée corrélation de Fermi. La corrélation de Coulomb, d'autre part, décrit la corrélation entre les positions spatiales des électrons de spin opposé à cause de la répulsion de Coulomb. Il y a également une corrélation liée à la symétrie globale ou au spin total du dispositif reconnu.
En termes simples, les orbitales moléculaires de la méthode Hartree-Fock sont optimisées en évaluant, dans chaque orbitale moléculaire, l'énergie d'un électron se déplaçant dans le champ moyen généré par les autres électrons, plutôt qu'en incluant la répulsion instantanée entre électrons.

Dispositifs cristallins

En physique de la matière condensée, les électrons sont typiquement décrits comparé à la trame périodique des noyaux atomiques. Les électrons non-interagissants sont décrits par des ondes de Bloch plutôt que par les orbitales utilisées dans les dispositifs atomiques et moléculaires. Un certain nombre d'approximations théoriques a été proposé pour expliquer les corrélations électroniques dans ces dispositifs cristallins.
Le modèle du liquide de Fermi des électrons corrélés dans les métaux peut expliquer la dépendance en température de la résistivité en termes d'interactions électron-électron.
La supraconductivité résulte des corrélations électroniques.
Le modèle de Hubbard est basé sur l'approximation <span class="citation">«tight-binding»</span>, et peut expliquer les transitions conducteur-isolant dans les isolants de Mott comme les oxydes de métaux de transition par la présence d'interactions de Coulomb répulsives entre les électrons.
L'interaction RKKY peut expliquer les corrélations électroniques de spin entre les électrons profonds non appariés dans différents atomes dans un cristal conducteur par une interaction de second ordre propagée par les électrons de conduction.
Le modèle du liquide de Luttinger-Tomonaga fait l'approximation des interactions électron-électron de second ordre comme des interactions bosoniques.

Considérations mathématiques

Pour deux électrons indépendants a et b,

,

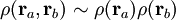où ρ (r_a, r_b) est la densité électronique jointe, ou la densité de probabilité de trouver l'électron a à r_a et l'électron b à r_b. Dans cette notation ρ (r_a, r_b) dr_adr_b réprésente la densité de probabilité de trouver les deux électrons dans leurs éléments de volume respectifs dr_a et dr_b.
Si ces deux électrons sont corrélés, la probabilité de trouver l'électron a à une certaine position de l'espace dépend de la position de l'électron b et vice versa. En d'autres termes, le produit de leurs fonctions de densité indépendantes ne décrit pas de manière correcte la situation réelle. À distances faibles, la densité de paire non-corrélée est trop importante; à distances importantes, elle est trop faible (i. e. les électrons «cherchent à s'éviter»).

Voir aussi

Cluster couplé interaction de configuration matériau fortement corrélé

méthode Hartree-Fock méthode de Monte-Carlo quantique méthode post-Hartree-Fock théorie de la perturbation de Møller-Plesset

• (en) Cet article est partiellement ou en totalité issu d'une traduction de l'article de Wikipédia en anglais intitulé «Electronic correlation».

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Corr%C3%A9lation_%C3%A9lectronique.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 12/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.