Champ multi-configurationnel auto-cohérent

Le champ multi-configurationnel auto-cohérent est une méthode de chimie quantique utilisée pour générer qualitativement des états de référence corrects pour des molécules dans les cas où la méthode Hartree-Fock...

Catégories :

Chimie quantique - Physique quantique - Chimie numérique

Source image : fr.wikipedia.org
Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur.

Page(s) en rapport avec ce sujet :

auto - cohérente avec des contraintes d'orthonormalité pour les orbitales.... La fonction d'onde de la méthode CI est une combinaison linéaire de déterminants de ... autocohérentes multi - configurationnelles (MCSCF pour "multiconfiguration...... et produisent un champ électrique polarisé dans le cœur du cristal.... (source : unige)
Ces fonctions sont généralement des orbitales atomiques, car centrées sur les ... Case quantique; Champ multi - configurationnel auto - cohérent ; Chimie.... (source : 7fr)

Méthodes numériques

pour le calcul de la structure électronique

Hartree-Fock

Théorie de la perturbation de Møller-Plesset

Interaction de configuration

Méthode du cluster couplé

Champ multi-configurationnel auto-cohérent

Théorie de la fonctionnelle de la densité

Le champ multi-configurationnel auto-cohérent (Multi-configurational self-consistent field - MCSCF) est une méthode de chimie quantique utilisée pour générer qualitativement des états de référence corrects pour des molécules dans les cas où la méthode Hartree-Fock et la théorie de la fonctionnelle de la densité ne sont pas pertinentes (comme par exemple pour les états fondamentaux moléculaires qui sont dégénérés avec des états excités bas ou dans les situations de rupture de liaisons). Il utilise une combinaison linéaire de fonctions d'état de configuration (CSF) ou des déterminants de configuration afin d'approximer la fonction d'onde électronique exacte d'un atome ou d'une molécule. Dans un calcul MCSCF, la totalité des cœfficients des CSF ou des déterminants et les fonctions de base dans les orbitales moléculaires sont modifiés afin d'obtenir la fonction d'onde électronique totale avec l'énergie la plus basse envisageable. Cette méthode peut être reconnue comme intermédiaire entre l'interaction de configuration (où les orbitales moléculaires ne sont pas modifiées mais la fonction d'onde étendue) et la méthode Hartree-Fock (dans laquelle il n'y a qu'un seul déterminant mais où les orbitales moléculaires fluctuent).
Les fonctions d'ondes MCSCF sont quelquefois utilisées comme états de référence pour une application des théories de configuration d'interaction multi-référence (MRCI) ou de perturbations multi-références comme perturbation de l'espace actif complet (CASPT2). Ces méthodes peuvent traiter des situations chimiques extrêmement complexes, et , si la puissance de calcul le permet, peuvent être utilisées pour calculer de manière fiable les états fondamentaux et excités moléculaires si les autres méthodes échouent.

Introduction

Dans le cas de la liaison simple la plus simple, celui de la molécule H₂, les orbitales moléculaires peuvent toujours s'écrire en termes de deux fonctions χ_iA and χ_iB (qui sont des orbitales atomiques avec des corrections faibles) situées sur les deux noyaux,

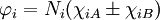$\varphi_i = N_i(\chi_{iA} \pm \chi_{iB})$ ,

où N_i est une constante de normalisation. La fonction d'onde de l'état essentiel pour H₂ à la géométrie d'équilibre est dominée par la configuration (φ₁) ², ce qui veut dire que l'orbitale moléculaire φ₁ est presque doublement occupée. Le modèle Hartree-Fock postule qu'elle est effectivement occupée, ce qui conduit à une fonction d'onde totale de :

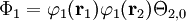$\Phi_1 = \varphi_1(\mathbf{r}_1)\varphi_1(\mathbf{r}_2)\Theta_{2,0}$ ,

dans laquelle Θ_{2, 0} est la fonction de spin (S=0) singulet pour deux électrons. Les orbitales moléculaires dans ce cas φ₁ sont prises comme sommes des orbitales atomiques 1s sur les deux atomes, c'est-à-dire : N₁ (1s_A+1s_B). Le développement de l'équation ci-dessus en orbitales atomiques donne :

$\Phi_1 = N_1ˆ2 \left[ 1s_A(\mathbf{r}_1)1s_A(\mathbf{r}_2) + 1s_A(\mathbf{r}_1)1s_B(\mathbf{r}_2) + 1s_B(\mathbf{r}_1)1s_A(\mathbf{r}_2) + 1s_B(\mathbf{r}_1)1s_B(\mathbf{r}_2) \right] \Theta_{2,0}$ .

Le modèle Hartree-Fock donne une description raisonnable de H₂ autour de la géométrie d'équillibre - soit à peu près une longueur de liaison d'environ 0, 735 Å (à comparer avec le 0, 746 Å de la valeur expérimentale) et 84 kcal/mol pour l'énergie de liaison (109 kcal/mol). Ces données sont typiques du modèle Hartree-Fock, qui décrit le plus souvent assez bien les dispositifs à couches fermées autour de leur géométrie d'équilibre. Pour des séparations importantes, cependant, les termes décrivant les électrons situés sur un atome persistent, ce qui correspond à la dissociation en H⁺ + H⁻, qui possède une énergie plus importante que H + H. Ainsi, la présence persistante de termes ioniques conduit à une solution non physique dans ce cas.
En conséquence, le modèle Hartree-Fock ne est parfois utilisé pour décrire les processus de dissociation avec des produits à couches ouvertes. La solution convenant le mieux à ce problème est d'introduire des cœfficients devant les différents termes dans Ψ₁ :

Ψ 1 = C I o n Φ I o n + C C o v Φ C o v

qui forme la base pour une description de la théorie de la liaison de valence des liaisons chimiques. Les cœfficients C_Ion et C_Cov variant, la fonction d'onde aura la forme correcte, avec C_Ion=0 pour la limite de séparation et C_Ion comparable à C_Cov à l'équilibre. Une telle description, cependant, utilise des fonctions de base non-orthogonales, ce qui complique sa structure mathématique. À la place, la multi-configuration est amenée en utilisant des orbitales moléculaires orthogonales. Après avoir introduit une orbitale anti-liante :

φ 2 = N 2 (1 s A - 1 s B)

la fonction d'onde totale de H₂ peut être rédigée comme une combinaison linéaire de configurations construites à partir d'orbitales liantes et anti-liantes :

Ψ M C = C 1 Φ 1 + C 2 Φ 2

où Φ₂ est la configuration électronique (φ₂) ². Dans cette description multi-configurationnelle de la liaison chimique dans H₂, C₁=1 and C₂=0 proche de l'équilibre, et C₁ sera comparable à C₂ pour les séparations importantes^[1].

Champ auto-cohérent dans l'espace actif complet

Une approche spécifiquement importante de la MCSCF est la méthode du champ auto-cohérent de l'espace actif complet (complete active space SCF method), dans laquelle une combinaison linéaire de CSF inclut tout ce qui résulte d'un nombre spécifique d'électrons dans un nombre spécifique d'orbitales. A titre d'exemple, on pourrait définir CASSCF (11, 8) pour une molécule, NO, dans laquelle les 11 électrons de valence sont distribués entre l'ensemble des configurations qui peuvent être construites à partir des 8 orbitales molécules^[2]^,^[3].

Champ auto-cohérent dans l'espace actif restreint

Le nombre de CSF croissant rapidement avec le nombre d'orbitales actives, en même temps que le coût numérique, il peut être indispensable d'utiliser un ensemble de CSF plus petit. Une manière de réaliser cette sélection est de restreindre le nombre d'électrons dans certains sous-espaces, ce qui est réalisé dans la méthode du champ auto-cohérent dans l'espace actif restreint (restricted active space SCF method - RASSCF). On peut, par exemple, permettre uniquement des excitations simples et doubles à partir de certains sous-ensembles fortement occupés d'orbitales actives, ou restreindre le nombre d'électrons à au plus 2 dans d'autres sous-ensembles d'orbitales actives.

Voir aussi

Charlotte Frœse Fischer
Douglas Hartree
Méthode Hartree-Fock

Références

↑ Roy McWeeny, Coulson's Valence, Oxford University Press, 124 - 129 p. (ISBN 0-19-855145-2)
↑ Frank Jensen, Introduction to Computational Chemistry, John Wiley and Sons, 133 - 158 p. (ISBN 0470011874)
↑ Christopher J. Cramer, Essentials of Computational Chemistry, John Wiley & Sons, Ltd., 191 - 232 p. (ISBN 0-471-48552-7)

Pour approfondir

Christopher J. Cramer, Essentials of Computational Chemistry, John Wiley and Sons (ISBN 0 471-48552 7)

(en) Cet article est partiellement ou en totalité issu d'une traduction de l'article de Wikipédia en anglais intitulé «Multi-configurational self-consistent field».

Recherche sur Amazone (livres) :

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Champ_multi-configurationnel_auto-coh%C3%A9rent.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 12/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.