Théorie de l'orbitale moléculaire
En chimie, la théorie de l'orbitale moléculaire est une méthode conçue pour la détermination d'une structure moléculaire dans laquelle les électrons ne sont pas assignés à des liaisons chimiques spécifiques entre les atomes, mais sont traités...
En chimie, la théorie de l'orbitale moléculaire (théorie OM ou théorie MO pour l'anglais molecular orbital) est une méthode conçue pour la détermination d'une structure moléculaire dans laquelle les électrons ne sont pas assignés à des liaisons chimiques spécifiques entre les atomes, mais sont traités comme se déplaçant sous l'influence des noyaux de la molécule dans son ensemble[1]. Dans cette théorie, chaque molécule est pourvue d'un ensemble d'orbitales moléculaires, dans lequel on postule que la fonction d'onde moléculaire ψf peut être rédigée comme une simple somme pondérée des n orbitales atomiques χi constitutives, selon l'équation suivante[2] :
Les cœfficients cij peuvent être déterminés numériquement en substituant de cette équation dans l'équation de Schrödinger et en appliquant le principe variationnel. Cette méthode est nommée approximation de la combinaison linéaire d'orbitales atomiques et est utilisée en chimie numérique. Une transformation unitaire supplémentaire peut être appliquée sur le dispositif afin d'accélérer la convergence de certains schémas de calculs. La théorie de l'orbitale moléculaire était perçue comme une rivale de la théorie de la liaison de valence dans les années 1930, avant qu'on réalise que ces méthodes étaient étroitement liées et qu'elles devenaient équivalentes quand elles étaient étendues.
Histoire
La théorie de l'orbitale moléculaire fut développée, dans les années suivant la construction de la théorie de la liaison de valence (1927), en premier lieu par les travaux de Friedrich Hund, Robert Mulliken, John C. Slater, et John Lennard-Jones[3]. Elle fut dans un premier temps nommée théorie de Hund-Mulliken[4]. Le terme d'orbitale fut introduit par Mulliken en 1932[4]. Courant 1933, la théorie de l'orbitale moléculaire était acceptée comme théorie validée et pratique[5]. Selon le physicien et physico-chimiste Erich Hückel, la première utilisation quantitative de la théorie de l'orbitale moléculaire fut l'article de 1929 de Lennard-Jones[6]. Le premier calcul précis d'une fonction d'onde moléculaire fut effectué en 1938 par Charles Coulson et portait sur la molécule de dihydrogène[7]. En 1950, les orbitales moléculaires étaient définies de manière aboutie comme fonctions propres (fonctions d'ondes) du hamiltonien du champ auto-cohérent et ce fut à partir de ce moment que la théorie de l'orbitale moléculaire devint pleinement rigoureuse et cohérente[8]. Cette approche rigoureuse est connue sous le nom de méthode Hartree-Fock pour les molécules quoiqu'elle soit basée sur les calculs atomiques. Dans les calculs sur les molécules, les orbitales moléculaires sont développées en termes d'une base d'orbitales atomiques, conduisant ainsi aux équations de Roothaan[9]. Ceci a conduit au développement de nombreuses méthodes ab initio de chimie quantique. En parallèle à ces développements rigoureux, la théorie de l'orbitale moléculaire est aussi appliquée dans une forme approchée utilisant des paramètres établis de manière empirique dans ce qui est connu sous le nom de méthodes quantique semi-empirique[10].
Description générale
La théorie de l'orbitale moléculaire (OM) utilise une combinaison linéaire d'orbitales atomiques pour former des orbitales moléculaires sur la molécule dans son ensemble. Elles sont quelquefois classées en orbitales liantes, orbitales antiliantes, et orbitales non-liantes. Une orbitale moléculaire est de fait une orbitale de Schrödinger incluant plusieurs, mais fréquemment uniquement deux, noyaux atomiques. Si cette orbitale est du type dans lequel les électrons de l'orbitale ont une plus grande probabilité de présence entre les noyaux qu'ailleurs, l'orbitale sera liante, et tendra à maintenir les noyaux ensemble. Si les électrons se situent plutôt dans une orbitale pour laquelle ils passent plus de temps ailleurs qu'entre les noyaux, l'orbitale sera antiliante et affaiblira la liaison. Les électrons des orbitales non-liantes se situent plutôt dans des orbitales profondes (presque des orbitales atomiques) associées presque dans leurs intégralités avec un noyau ou l'autre, et ainsi passent tout autant de temps entre les noyaux qu'ailleurs. Ces électrons n'affaiblissent ni ne renforcent les liaisons chimiques.
Les orbitales moléculaires sont aussi divisées selon le types d'orbitales atomiques combinées pour former une liaison. Ces orbitales sont le résultat des interactions électron-noyau causées par la force principale électromagnétique. Les produits chimiques forment une liaison si leurs orbitales deviennent plus basse en énergie quand elles interagissent ensemble. Les différentes liaisons chimiques se distinguent par la forme de leur nuage électronique et leurs niveaux d'énergies.
La théorie OM procure un aperçu global et délocalisé sur la liaison chimique. A titre d'exemple, dans la théorie OM pour les molécules hypervalentes, il n'est plus indispensable de considérer un rôle majeur pour les orbitales d. Dans la théorie OM, tout électron de la molécule peut être situé partout sur la molécule, les conditions quantiques permettant aux électrons de se déplacer sous l'influence d'un grand nombre arbitraire de noyaux, dans la limite des règles de sélectivité. Quoique dans la théorie OM certaines orbitales moléculaires peuvent comprendre des électrons qui sont situés particulièrement entre certaines paires d'atomes moléculaires, d'autres orbitales comprennent des électrons dispersés plus uniformément sur la molécule. De fait, les liaisons (et les électrons) sont énormément plus délocalisées dans la théorie OM que ce qui est indiqué par la théorie de la liaison de valence : cela rend la théorie OM plus pratique pour la description des dispositifs étendus.
Un exemple est la description OM du benzène, dont la structure est un cycle hexagonal de 6 atomes de carbone. Dans cette molécule, 24 des 30 électrons liants de valence sont situés dans 12 orbitales liantes σ (sigma) essentiellement localisées entre les paires d'atomes (C-C et C-H), comme présenté par la théorie de la liaison de valence. Cependant, dans le benzène, les 6 électrons restants sont situés dans trois orbitales moléculaires liantes π (pi) délocalisées sur le cycle. Deux se placent dans une orbitale moléculaire qui a des contributions identiques des six atomes. Les deux autres ont des neux verticaux à angles droits entre eux. Comme dans la théorie de la liaison de valence, ces six électrons π délocalisés se situent dans les grands espaces existant en dessous et au dessus du plan du cycle. L'ensemble des liaisons carbone-carbone dans le benzène sont chimiquement équivalentes. Dans la théorie OM, c'est une conséquence directe du fait que les trois orbitales π forment une combinaison qui distribue les 6 électrons «surnuméraires» sur les 6 atomes de carbone[11].
Dans des molécules comme le méthane (CH4), les 8 électrons de valence sont dans 4 orbitales moléculaires réparties sur la totalité des 5 atomes constitutifs. Cependant, il est envisageable de transformer ce point de vue, sans modifier ni la fonction d'onde totale, ni l'énergie, en 8 électrons dans 4 orbitales situées identiques à l'image «normale» de liaisons covalentes à deux électrons. C'est ce qui a été fait ci-dessus pour les liaisons σ du benzène, mais reste impossible pour les orbitales π. L'image délocalisée est plus appropriée pour la description des propriétés d'ionisation et spectroscopiques. Lors d'une ionisation, un électron unique est pris à la molécule dans son ensemble. L'ion résultant ne possède pas de liaison se distinguant des autres. De manière identique pour le cas des excitations électroniques, l'électron excité est délocalisé sur la molécule dans son ensemble et non pas situé sur une liaison spécifique.
D'autres composés comme le β-carotène ou substances comme la chlorophylle ou les hèmes présentent à l'instar du benzène des électrons π dans des orbitales moléculaires sur la totalité de la molécule, donnant la possibilité une augmentation de l'absorption lumineuse pour de faibles énergies (spectre visible), ce qui est de fait observé. Ce fait, mais aussi d'autres caractéristiques spectroscopiques pour des molécules est bien expliqué dans la théorie de l'orbitale moléculaire, avec un accent porté sur les états électroniques associés aux orbitales multicentres, y compris les «mélanges» d'orbitales déduit des principes de correspondance de symétrie orbitalaire. Les mêmes principes d'orbitales moléculaires expliquent aussi de manière naturelle certains phénomènes électriques, comme la haute conductivité électrique dans la direction du plan des feuillets hexagonaux du graphite. Dans la théorie OM, la «résonance» (mélange et recouvrement des états de la liaison de valence) est une conséquence naturelle de la symétrie. Ainsi, dans le graphite comme dans le benzène, il n'est pas indispensable de postuler l'hybridation sp2 et la résonance de la théorie de la liaison de valence afin d'expliquer la conduction électrique. Au lieu de cela, la théorie OM indique simplement que certains électrons dans les feuillets atomiques sont totalement délocalisés sur des distances arbitraires, et se situent sur de particulièrement grandes «orbitales moléculaires» recouvrant le plan graphitique en entier, donnant la possibilité ainsi à certains électrons de se mouvoir et de conduire l'électricité dans le plan graphitique, comme s'ils appartenaient à un métal.
Voir aussi
Références
- ↑ Daintith, J. (2004). Oxford Dictionary of Chemistry. New York : Oxford University Press. ISBN 0-19-860918-3.
- ↑ Licker, Mark, J. (2004). McGraw-Hill Concise Encyclopedia of Chemistry. New York : McGraw-Hill. ISBN 0-07-143953-6.
- ↑ Coulson, Charles, A. (1952). Valence. Oxford at the Clarendon Press.
- ↑ a b (en) Spectroscopy, Molecular Orbitals, and Chemical Bonding - Discours Nobel de Robert Mulliken (1966).
- ↑ (en) Lennard-Jones Paper of 1929 - Foundations of Molecular Orbital Theory.
- ↑ Hückel, E. (1934). Trans. Faraday Soc. 30, 59.
- ↑ Coulson, C. A. (1938). Proc. Camb. Phil. Soc. 34, 204.
- ↑ Hall, G. G. Lennard-Jones, Sir John. (1950). Proc. Roy. Soc. A202, 155.
- ↑ Frank Jensen, Introduction to Computational Chemistry, John Wiley and Sons, 1999, p. 65 - 69, ISBN 0 471 98055
- ↑ Frank Jensen, Introduction to Computational Chemistry, John Wiley and Sons, 1999, p. 81 - 92, ISBN 0 471 98055
- ↑ (en) Introduction to Molecular Orbital Theory - Imperial College London
Liens externes
- (en) Molecular Orbital Theory - Purdue University
- (en) Molecular Orbital Theory - Sparknotes
- (en) Molecular Orbital Theory - Mark Bishop's Chemistry Site
- (en) Introduction to MO Theory - Queen Mary, London University
- (en) Molecular Orbital Theory - a related terms table
- (en) Cet article est partiellement ou en totalité issu d'une traduction de l'article de Wikipédia en anglais intitulé «Molecular orbital theory».
Recherche sur Google Images : |
|
"Théorie de l'orbitale moléculaire - ..." L'image ci-contre est extraite du site fr.wikipedia.org Il est possible que cette image soit réduite par rapport à l'originale. Elle est peut-être protégée par des droits d'auteur. Voir l'image en taille réelle (111 x 47 - 1 ko - png)Refaire la recherche sur Google Images |
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

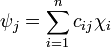

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité