Pseudo-potentiel

En chimie quantique, la méthode du pseudo-potentiel (ou pseudopotentiel) est une tentative pour remplacer le potentiel d'interaction coulombien du noyau et les effets des électrons de cœur, fortement liés, par un potentiel effectif interagissant seulement avec les électrons de valence. L'approximation du pseudopotentiel présente un grand intérêt dans le calcul théorique de la structure électronique de la matière car elle sert à ne traiter explicitement que les électrons de valence ; donnant la possibilité ainsi un gain important dans les ressources informatiques nécessaires aux calculs. Un pseudopotentiel peut être généré pour un atome dans une configuration électronique de référence choisie arbitrairement. Il est ensuite utilisé dans les calculs des propriétés des électrons de valence pour d'autres dispositifs (molécules, solides …)  ; la description des états de cœur restant inchangés quel que soit le dispositif étudié. Le schéma qui sert à générer un pseudopotentiel n'est pas unique ce qui explique le développement de plusieurs classes de pseudopotentiels surtout les pseudopotentiels dits «à norme conservée» et «ultrasoft» (appelés quelquefois pseudopotentiels de Vanderbilt).

L'approche du pseudopotentiel

L'approche du pseudopotentiel est basée sur le fait qu'une grande majorité des propriétés physiques et chimiques des matériaux ne dépendent que du comportement des électrons de valence. En effet, dans un atome seuls les électrons de périphériques (en petit nombre) contribuent à la formation des liaisons chimiques tandis que les électrons de cœur (en grand nombre) sont eux fortement liés au noyau atomique et par conséquent peu sensible à l'environnement proche de l'atome. La distribution des électrons de cœur peut par conséquent être reconnue comme quasiment inchangée même quand l'atome est positionné dans un milieu chimique différent de celui de l'atome isolé. C'est sur cette propriété que se fonde l'approximation dite du cœur gelé (frozen-core approximation) qui consiste à calculer, pour l'atome isolé, la configuration électronique de l'ion. L'avantage de cette approximation est que le nombre d'électron apparaissant de manière explicite dans les calculs (et par conséquent le nombre d'équation à résoudre) s'en trouve fortement réduit; seuls les électrons de valence sont pris en compte (a titre d'exemple, pour un cristal de 100 atomes de silicium on passe de 1400 à 400 électrons).
Si l'approche du cœur gelé forme une avancée importante dans l'optique d'une gain dans les ressources informatiques son application telle qu'énoncée plus haut n'est pas souhaitable. En effet, les électrons de cœur apparaissent toujours de manière implicite. Or, en mécanique quantique l'ensemble des fonctions d'onde décrivant les états électroniques (c'est-à-dire les électrons) doivent être orthogonales entre elles (condition d'orthogonalité généralisée). Cette condition impose à la fonction d'onde de valence d'être orthogonale à l'ensemble des fonctions d'onde décrivant les états de cœur. Cette contrainte fait que la fonction d'onde de valence présente une structure nodale peut favorable d'un point de vue numérique^[1]. Il est par conséquent plus judicieux de remplacer le véritable ion de cœur par un potentiel ionique effectif auquel est associé une fonction d'onde adoucie (c'est-à-dire sans nœud). L'emploi d'un potentiel effectif se justifie par la nature quantique des électrons qui est telle que le potentiel répulsif généré par les électrons de cœur est compensé par le potentiel attractif du noyau (cancellation theorem). Il en résulte un potentiel ionique effectif assez doux qui n'agit que sur les électrons de valence; le pseudopotentiel.

Pseudopotentiel empirique

Le concept de pseudopotentiel a été introduit dans les années 1930 par Fermi ^[2]. Par la suite, Hellmann utilise cette notion pour le calcul des niveaux énergétiques de métaux alcalins ^{[3], [4]}. Ces premiers pseudopotentiels sont qualifiés d'empiriques; ce qui veut dire qu'ils ne sont pas obtenus par calcul mais paramétrés pour reproduire au mieux des résultars expérimentaux de référence. L'utilisation d'un tel type de pseudopotentiel se fonde sur deux constatations. Dans un premier temps, s'il était certain à cette époque qu'on pouvait obtenir de manière exacte et par calcul des pseudopotentiels cela passait par la résolution de calculs complexes (impliquant les fonction d'onde atomiques) impossible à résoudre sans ressources informatiques. L'utilisation d'une méthode empirique bien plus simple allait par conséquent de soi. Par la suite, on peut constater qu'un certain nombre d'éléments peuvent être décrit par des pseudopotentiels paramétrisés tout en fournissant une approximation acceptable de l'interaction électron de valence - ion de cœur. Cela était vrai surtout pour les métaux alcalins, les métaux "simples" tels que l'aluminium mais aussi les semi-conducteurs. L'utilisation de ces pseudopotentiels va permettrent en une dizaine d'année d'augmenter le champ des connaissances dans le domaine de l'état solide avant d'être remplacé par des pseudopotentiels ab initio plus efficaces.

Méthode des ondes planes orthogonales

La méthode des ondes planes orthogonales (OPW pour orthogonalized planes waves) a été introduite par Convers Herring dans les années 1940^[5]. La méthode permit de mieux comprendre la nature de structure de bande de matériaux semiconducteurs tels que le silicium et le germanium et fut la première à expliquer de manière théorique que le silicium est un matériau à gap indirect^[6]. Le développement de cette méthode mérite d'être introduit car celle-ci est l'ancêtre direct de la notion de pseudopotentiel.

Formalisme mathématique

De manière concrète, la méthode OPW est une approche générale qui vise à construire des fonctions de bases pour la description des états de valence. Ces fonctions sont définies de la manière suivante :

[5]

«This suggest that it would be practical to try to approximate [the eigenfunction] by a linear combinaison of a few planes waves, plus a linear combinaison of a few function u_j localized about each nucleus and obeying wave equations of the form :

»

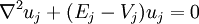
Le potentiel Vj et les fonctions uj qui apparaissent dans l'équation doivent être choisie de manière optimales. Il est important de préciser que, les états de valence étant étiquetés, par leurs nombres quantiques l et m, il est normal que les fonctions qu'on ajoute possèdent aussi les mêmes valeurs de l et m. Des précédentes définitions, les fonctions d'onde de valence peuvent être exprimées comme :

Pseudopotentiel de Phillips-Kleinman-Antoncik

C'est par une reformulation de la méthode OPW d'Herring qu'en 1959 Phillips et Kleinman développent la première approche formelle (non empirique) de la notion de pseudopotentiel^[7]. Antoncik, de manière indépendante, publie la même année une approche identique. ^[8] La méthode du pseudopotentiel de Phillips-Kleinman-Antoncik (PKA) est la première à montrer que la condition d'orthogonalité dans la région de cœur entre les états de cœur et de valence agit comme un potentiel répulsif qui tend à s'oppœr au potentiel nucléaire attractif ressentit par les électrons de valence. Le plus fréquemment, ces deux effets se combinent pour former un potentiel faiblement répulsif, le pseudopotentiel^[9].

Avantages et inconvénients

Pseudopotentiel à norme conservée

L'introduction du principe de pseudopotentiel à norme conservée représente la percée la plus significative dans le traitement des électrons de cœur. L'approche fut développée par Hamann, Schlüter et Chiang^[10] et fut suive peu de temps après par une méthode particulièrement identique mais établie de manière indépendante par Kerker^[11].

Méthodologie

La première étape dans la génération d'un pseudopotentiel à norme conservée consiste à réaliser un calcul atomique ab initio tous-électrons. La configuration électronique de l'atome peut être choisie arbitrairement. Le plus souvent il s'agit de l'atome à l'état neutre. Le calcul se fait au départ de l'équation de Khon-Sham rédigée sous sa forme radiale :

La fonction d'onde réelle est ensuite remplacée par une pseudofonction d'onde à laquelle est associée un potentiel modèle (le pseudopotentiel) choisi pour reproduire correctement les propriétés des états de valence. Le schéma mathématique qui sert à générer la pseudofonction d'onde n'est pas unique. Il existe du point de vue mathématique une certaine liberté dans le choix de la méthode comme en témoignent les nombreuses publications qui présentent différentes manière de faire^{[10], [11], [12], [13], [14], [15], [16], [17]}.

Conditions sur la pseudofonction

Pour obtenir un pseudopotentiel à norme conservée le plus efficace envisageable, la pseudofonction d'onde doit répondre à une liste de critère précis^[10].

• Les énergies propres obtenus par un calcul tout électron et les pseudoénergies sont identiques pour une configuration atomique de référence.
• Les pseudofonctions d'onde de valence et les fonctions d'onde de valence tout électron sont semblables au-delà d'un certain rayon de cœur r_C choisi arbitrairement.
• L'intégration de 0 à r_C pour chaque fonction d'onde est semblable (condition de conservation de la norme)
• Les dérivées logarithmiques de la fonction d'onde tout électron et de la pseudofonction d'onde mais aussi leur dérivée première comparé à l'énergie sont identiques pour tout r ≥ r_C.

Relations mathématiques

Note : dans les formules suivantes, les notations Æ et PS font référence respectivement aux résultats obtenus de manière ab initio et avec le pseudopotentiel.
Φ représente la fonction d'onde

1. ε^PS = ε^AE 2. Φ^PS (r) = Φ^AE (r) pour r > r_C 3.

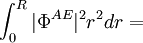
à compléter...

Prise en compte des effets relativistes

Etats fantômes

Références

Note : Les articles scientifiques sont consultables au format [pdf] uniquement pour les abonnées à ces revues. Les abstracts des articles sont cependant accessibles à tous.

1. ↑ Les fonctions d'onde sont décrites sur des bases d'ondes planes. Plus la foncion d'onde possède de nœud, plus le nombre d'ondes planes impliqués est important ce qui accroit fortement le temps de calcul
2. ↑ (en) E. fermi, «», dans Nuovo Cimento, vol.  11, 1934, p.  157
3. ↑ (en) H. Hellmaan, «A New Approximation Method in the Problem of Many Electrons», dans The Journal of Chemical Physics, vol.  3, 1935, p.  61 [lien DOI]
4. ↑ H. Hellmann and W. Kassatotschkin (1925) Acta Physicochim. U. R. S. S. 5, 23
5. ↑ ^{a  b}  (en) W. C. Herring, «A new method for calculating wave functions in crystal», dans Phys. Rev. , vol.  57, 1940, p.  1169-1177 [lien DOI]
6. ↑ (en) F. Bassani, «Energy band structure in silicon crystals by the orthogonalized plane-wave method», dans Phys. Rev. , vol.  108, 1957, p.  263-264 [lien DOI]
7. ↑ (en) J. C. Phillips and L. Kleinman, «New Method for Calculating Wave Functions in Crystals and Molecules», dans Phys. Rev. , vol.  116, 1959, p.  287-294 [lien DOI]
8. ↑ E. Antoncik (1959) J. Phys. Chem. Solids 10, 314
9. ↑ Quoique la publication de Phillips et Kleinman soit reconnue historiquement comme la première dans le domaine des pseudopotentiels (non empirique) le terme pseudopotentiel n'apparait pas une seule fois. Seul le terme potentiel effectif répulsif est employé.
10. ↑ ^{a  b  c}  (en) D. R. Hamann, M. Schlüter, C. Chiang, «Norm-Conserving Pseudopotentials», dans Phys. Rev. Lett. , vol.  43, 1979, p.  1494-1497 [lien DOI]
11. ↑ ^{a  b}  (en) J. P. Kerker, «Non-singular atomic pseudopotentials for solid state applications», dans J. Phys. C : Solid State Phys. , vol.  13, 1980, p.  L189-L194 [lien DOI]
12. ↑ (en) G. B. Bachelet *, D. R. Hamann, and M. Schlüter, «Pseudopotentials that work : From H to Pu», dans Phys. Rev. B, vol.  43, 1982, p.  4199-4228 [lien DOI]
13. ↑ (en) D. Vanderbilt, «Optimally smooth norm-conserving pseudopotentials», dans Phys. Rev. B, vol.  32, 1985, p.  8412-8416 [lien DOI]
14. ↑ (en) N. Troullier and J. L. Martins, «A straightforward method for generating soft transferable pseudopotentials», dans Solid State Comm. , vol.  74, 1990, p.  613-616 [lien DOI]
15. ↑ (en) N. Troullier and J. L Martins, «Efficient pseudopotentials for plane-wave calculations», dans Phys. Rev. B, vol.  43, 1991, p.  1993-2005 [lien DOI]
16. ↑ (en) S. Gœdecker, M. Teter, and J. Hutter, «Separable dual-space Gaussian pseudopotentials», dans Phys. Rev. B, vol.  54, 1996, p.  1703-1710 [lien DOI]
17. ↑ (en) C. Hartwigsen, S. Gœdecker, and J. Hutter, «Relativistic separable dual-space Gaussian pseudopotentials from H to Rn», dans Phys. Rev. B, vol.  58, 1998, p.  3641-3662 [lien DOI]

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Pseudo-potentiel.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.