Conditions d'Eckart
Les conditions d'Eckart, appelées selon le physicien américain Carl Eckart, et nommées quelquefois conditions de Sayvetz, permettent la simplification de l'équation de Schrödinger du mouvement nucléaire lors de la seconde étape de l'approximation de Born-Oppenheimer.
Recherche sur Google Images :
Source image : fr.wikipedia.org Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- On rappelle la définition des coordonnées d'Eckart pour un dispositif de N... d'une voie de dissociation se fait au moyen d'un vecteur unitaire de RN-1, Γ, ... (source : jphys.journaldephysique)
Les conditions d'Eckart[1], appelées selon le physicien américain Carl Eckart, et nommées quelquefois conditions de Sayvetz[2], permettent la simplification de l'équation de Schrödinger du mouvement nucléaire (rovibrationnel) lors de la seconde étape de l'approximation de Born-Oppenheimer. Les conditions d'Eckart permettent dans une large mesure la séparation des modes externes des modes internes. Quoique les mouvements de rotation et de vibration des noyaux dans une molécule ne puissent être totalement scindés, les conditions d'Eckart minimisent le couplage entre ces mouvements.
Définition des conditions d'Eckart
Les conditions d'Eckart peuvent uniquement être formulées pour une molécule semi-rigide, qui est une molécule avec une surface d'énergie potentielle V (R1, R2, .. RN) possédant un minimum défini exactement pour RA0 (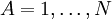 ). Ces coordonnées d'équilibre des noyaux - de masses MA sont exprimées dans un repère à axes principaux orthonormés fixes et satisfont par conséquent les relations :
). Ces coordonnées d'équilibre des noyaux - de masses MA sont exprimées dans un repère à axes principaux orthonormés fixes et satisfont par conséquent les relations :
λi0 est ici un des moments d'inertie principaux de la molécule à l'équilibre. Les triplets RA0 = (RA10, RA20, RA30) satisfaisant ces conditions, intègrent la théorie comme ensemble donné de constantes réelles. À l'instar de Biedenharn et Louck[3], on introduit un repère orthonormé fixe, le repère d'Eckart,
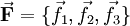 .
.
Si on est lié au repère d'Eckart, qui - suivant la molécule - tourne et translate dans l'espace, on observerait la molécule dans sa géométrie d'équilibre quand on fixe les noyaux à ces points
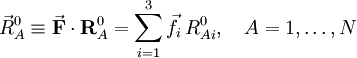 .
.
On choisit les éléments de RA comme coordonnées dans le repère d'Eckart du vecteur position du noyau A (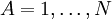 ). Si on prend l'origine du repère d'Eckart au centre de masse instantané, les relations suivantes sont vérifiées :
). Si on prend l'origine du repère d'Eckart au centre de masse instantané, les relations suivantes sont vérifiées :
On définit alors les coordonnées de déplacement :
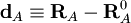 .
.
Ces coordonnées de déplacement satisfont les conditions de translation d'Eckart,
Les conditions de rotation d'Eckart pour les déplacements sont :
où 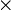 indique un produit vectoriel.
indique un produit vectoriel.
Ces conditions de rotation proviennent de la construction spécifique du repère d'Eckart (voir Biedenharn et Louck, loc. cit. , page 538). Enfin, pour une meilleure compréhension du repère d'Eckart, il peut être utile de remarquer qu'il devient un repère selon les axes principaux dans le cas où la molécule est un rotateur rigide, soit quand les N vecteurs de déplacement sont nuls.
Séparation des coordonnées internes et externes
Les N vecteurs positions 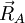 des noyaux forment un espace linéaire à 3 dimensions R3N : l'espace de configuration. Les conditions d'Eckart donnent une décomposition de somme orthogonale directe de cet espace :
des noyaux forment un espace linéaire à 3 dimensions R3N : l'espace de configuration. Les conditions d'Eckart donnent une décomposition de somme orthogonale directe de cet espace : 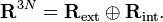 Les éléments du sous-espace de dimension 3N-6 Rint se rapportent aux coordonnées internes, car invariantes quelle que puisse être les rotations ou translations d'ensemble de la molécule et , par conséquent, dépendant seulement des mouvements internes (vibrationelles). Les éléments du sous-espace à 6 dimensions Rext rapportent aux coordonnées externes, car associés avec les translations et rotations d'ensemble de la molécule.
Les éléments du sous-espace de dimension 3N-6 Rint se rapportent aux coordonnées internes, car invariantes quelle que puisse être les rotations ou translations d'ensemble de la molécule et , par conséquent, dépendant seulement des mouvements internes (vibrationelles). Les éléments du sous-espace à 6 dimensions Rext rapportent aux coordonnées externes, car associés avec les translations et rotations d'ensemble de la molécule.
Pour clarifier la nomenclature, on définit en premier lieu une base pour Rext. Pour cela on introduit les six vecteurs suivants (i = 1, 2, 3) :
Une base orthogonale, non normalisée, pour Rext est :
Un vecteur de déplacement pondéré peut alors être rédigé :
Pour i=1, 2, 3,
où le zéro provient de l'application des conditions de translation d'Eckart. Pour i=4, 5, 6
où le zéro provient de l'application des conditions de rotation d'Eckart. On en déduit que le vecteur de déplacement 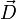 appartient au complémentaire orthogonal de Rext, par conséquent forme un vecteur interne.
appartient au complémentaire orthogonal de Rext, par conséquent forme un vecteur interne.
On obtient une base pour le sous-espace en définissant 3N-6 vecteurs linéairement indépendants : 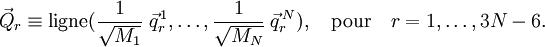 Les vecteurs
Les vecteurs 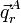 peuvent être des vecteurs s de Wilson ou peuvent être obtenus dans l'approximation harmonique en diagonalisation le hessien de V. On introduit alors les modes internes (de vibration).
peuvent être des vecteurs s de Wilson ou peuvent être obtenus dans l'approximation harmonique en diagonalisation le hessien de V. On introduit alors les modes internes (de vibration).
La signification physique de qr dépend des vecteurs 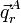 . A titre d'exemple, qr peut être un mode symétrique d'étirement, dans lesquels deux liaisons C-H sont simultanément étirées et contractées.
. A titre d'exemple, qr peut être un mode symétrique d'étirement, dans lesquels deux liaisons C-H sont simultanément étirées et contractées.
On a vu que les modes externes correspondants sont nuls à cause des conditions d'Eckart,
Translation et rotation globale
Les modes de vibration (internes) sont invariant par translation et rotation illimitétésimale de la molécule à l'équilibre (référence) si et uniquement si les conditions d'Eckart s'appliquent. Cela est démontré dans cette partie.
Une translation globale de la molécule de référence est donnée par :
pour un tri-vecteur 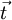 abritraire.
abritraire.
Une rotation illimitétésimale de la molécule est décrite par :
où Δφ est un angle illimitétésimal, Δφ >> (Δφ) ², et 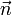 est un vecteur unitaire arbitraire. L'orthogonalité de
est un vecteur unitaire arbitraire. L'orthogonalité de 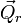 à l'espace externe implique que
à l'espace externe implique que 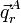 satisfasse :
satisfasse :
Maintenant, par translation :
Ainsi, 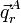 est invariant par translation si et uniquement si :
est invariant par translation si et uniquement si :
car le vecteur 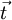 est arbitraire. Donc, les conditions sur les translations d'Eckart impliquent l'invariance transitionnelle des vecteurs appartenant à l'espace interne et vice versa. Par rotation, on a :
est arbitraire. Donc, les conditions sur les translations d'Eckart impliquent l'invariance transitionnelle des vecteurs appartenant à l'espace interne et vice versa. Par rotation, on a :
L'invariance par rotation s'ensuit si et uniquement si :
Les modes externes, d'autre part, ne sont pas invariants et il n'est pas complexe de montrer qu'ils sont modifiés par translation comme ci-après :
où M est la masse totale de la molécule. Ils sont modifiés par rotation illimitétésimale comme il suit :
où I0 est le tenseur d'inertie de la molécule à l'équilibre. Ce comportement indique que les trois premiers modes externes décrivent la translation d'ensemble et les trois derniers la rotation d'ensemble.
Énergie de vibration
L'énergie de vibration d'une molécule peut être rédigée en termes de coordonnées comparé au repère d'Eckart comme :
Le repère d'Eckart n'étant pas galiléen, l'énergie cinétique totale comprend aussi les termes de rotation et de Coriolis, qu'on considère comme implicites ensuite. L'énergie de vibration est rédigée en termes de coordonnées de déplacment, qui sont linéairement dépendantes car influées par les 6 modes externes, nuls, i. e. les dA satisfont à 6 relations linéaires. Il est envisageable d'écrire l'énergie de vibration seulement en termes de modes internes qr (r =1, ..., 3N-6) comme il va être montré ensuite. On rédigé les différents modes en termes de déplacements
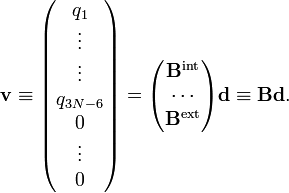
Les expressions entre parenthèses définissent une matrice B liant les modes internes et externes aux déplacements. la matrice B peut être divisée en une partie interne (3N-6 x 3N) et une partie externe (6 x 3N)
On définit la matrice M par :
et à partir des relations données auparavant on obtient les relations matricielles :
et
On définit
En utilisant les règles de multiplication des matrices par blocs, on montre que :
où G-1 est de dimension (3N-6 x 3N-6) et N-1 de dimension (6 x 6). Lénergie cinétique devient :
où les six derniers composants sont nuls. Cette forme de l'énergie cinétique de vibration est membre de la méthode GF de Wilson. Il est intéressant de signaler que l'énergie potentielle dans l'approximation harmonique peut être rédigée de la façon suivante :
où H est le hessien du potentiel au minimum et F, défini par cette équation, est la matrice F de la méthode GF.
Relation à l'approximation harmonique
Dans l'approximation harmonique du problème de vibration nucléaire, exprimée en coordonnées de déplacement, on doit résoudre le problème le problème du polynôme de Jacobi :
où H est une matrice 3N x 3N symétrique des dérivées secondes du potentiel 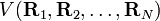 . H est la matrice hessienne de V à l'équilibre
. H est la matrice hessienne de V à l'équilibre 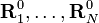 . La matrice diagonale M a pour cœfficients non nuls les masses.
. La matrice diagonale M a pour cœfficients non nuls les masses.
La matrice diagonale  contient les valeurs propres, tandis que les colonnes de C contient les vecteurs propres. On peut montrer que l'invariance de V par translation simultanée de t de l'ensemble des noyaux implique que les vecteurs T = (t, ..., t) sont dans le noyau (mathématique) de H. L'invariance de V par rotation illimitétésimale s d'ensemble de l'ensemble des noyaux montre que les vecteurs S = (s x R10, ..., s x RN0) appartiennent aussi au noyau de H :
contient les valeurs propres, tandis que les colonnes de C contient les vecteurs propres. On peut montrer que l'invariance de V par translation simultanée de t de l'ensemble des noyaux implique que les vecteurs T = (t, ..., t) sont dans le noyau (mathématique) de H. L'invariance de V par rotation illimitétésimale s d'ensemble de l'ensemble des noyaux montre que les vecteurs S = (s x R10, ..., s x RN0) appartiennent aussi au noyau de H :
Donc, 6 colonnes de C correspondant à la valeur propre nulle, sont déterminés algébriquement. Si le problème généralisé des valeurs propres est résolu numériquement, on trouve le plus souvent 6 combinaisons linéairement indépendantes de S et T). L'espace propre correspondant à la valeur propre nulle est au moins de dimension 6 (il est quelquefois précisément de dimension 6, qui sont les constantes de force, ne sont jamais nulles pour des molécules dans leur état essentiel). T et S correspondant alors aux mouvements externes (dans leur ensemble) : translation et rotation, respectivement. Ils sont les modes d'énergie nulle car l'espace est homogène (sans force) et isotrope (sans torsion).
Par définition, les modes de fréquence nulle sont des modes internes, appartenant au complémentaire orthogonal de Rext. Les orthogonalisations généralisées : 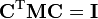 appliquées aux colonnes «internes» (valeurs propres non nulles) et «externes» (valeur propre nulle) de C sont équivalents aux conditions d'Eckart.
appliquées aux colonnes «internes» (valeurs propres non nulles) et «externes» (valeur propre nulle) de C sont équivalents aux conditions d'Eckart.
Références
- ↑ C. Eckart, Some studies concerning rotating axes and polyatomic molecules, Physical Review, vol. 47, p. 552-558 (1935).
- ↑ Aaron Sayvetz, The Kinetic Energy of Polyatomic Molecules, J. Chem. Phys. vol. 7, pp. 383-389 (1939).
- ↑ L. C. Biedenharn and J. D. Louck, Angular Momentum in Quantum Physics, Addison-Wesley, Reading (1981) p. 535.
Bibliographie
- E. Bright Wilson, Jr., J. C. Decius et Paul C. Cross, Molecular Vibrations, Mc-Graw-Hill (1955). Réimprimé par Dover (1980).
- D. Papoušek et M. R. Aliev, Molecular Vibrational-Rotational Spectra, Elsevier (1982).
- S. Califano, Vibrational States, Wiley, New York-London (1976). ISBN 0 471 12996 8
- (en) Cet article est partiellement ou en totalité issu d'une traduction de l'article de Wikipédia en anglais intitulé «Eckart conditions».
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 12/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

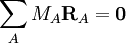
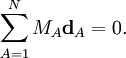
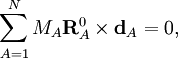
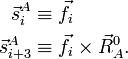
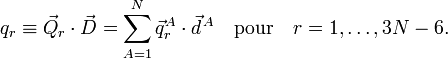
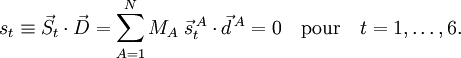
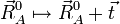
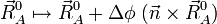
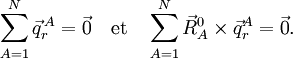
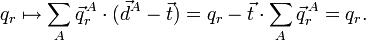
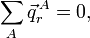
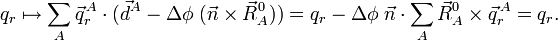
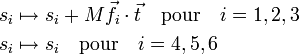
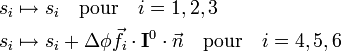
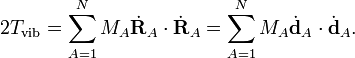
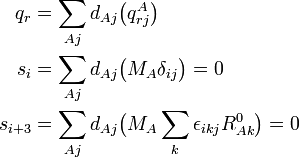
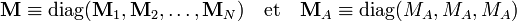
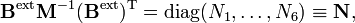
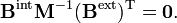
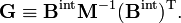
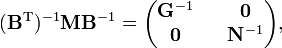
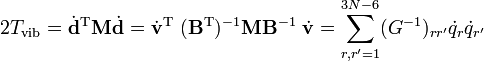
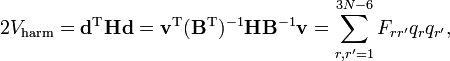
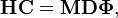
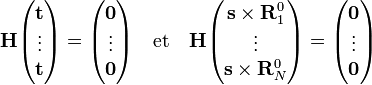

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité