Interaction de configuration
L'interaction de configuration est une méthode post-Hartree-Fock linéaire variationnelle pour la résolution de l'équation de Schrödinger non relativiste dans l'approximation de Born-Oppenheimer pour un dispositif chimique quantique multi-électronique.
Recherche sur Google Images :

Source image : iramis.cea.fr Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- La méthode LCAO perfectionnée a été utilisée pour l'étude de la structure électronique des .... Cependant, comme 1'interaction de configuration est un calcul de ... (source : linkinghub.elsevier)
- La param6trisation de la methode CNDOIS utilisee a ete... L'interaction de configuration est limitie aux 30 configura- de la geometric... (source : article.pubs.nrc-cnrc.gc)
- Les sections de choc obtenue par les dif/érentes méthodes sont discutées....... L'équation précédente est sans interaction de configuration, et ii n'y a qu'une equation..... dans le cas oi'i l'interaction de configuration est faible, ... (source : adsabs.harvard)
| Méthodes numériques
pour le calcul de la structure électronique |
| Hartree-Fock |
| Théorie de la perturbation de Møller-Plesset |
| Interaction de configuration |
| Méthode du cluster couplé |
| Champ multi-configurationnel auto-cohérent |
| Théorie de la fonctionnelle de la densité |
L'interaction de configuration (configuration interaction en anglais - CI) est une méthode post-Hartree-Fock linéaire variationnelle pour la résolution de l'équation de Schrödinger non relativiste dans l'approximation de Born-Oppenheimer pour un dispositif chimique quantique multi-électronique. Deux sens sont liés à l'expression d'«interaction de configuration» dans ce contexte. Mathématiquement, le terme de configuration décrit simplement la combinaison linéaire de déterminants de Slater utilisée pour la fonction d'onde. En termes de spécification de l'occupation des orbitales (par exemple 1s2 2s2 2p1... ), le mot interaction veut dire le mélange (interaction) de différentes configurations électroniques (états). À cause des temps de calculs nécessaires et du matériel requis pour des calculs CI, cette méthode est restreinte à des dispositifs assez petits.
Au contraire de la méthode Hartree-Fock, la CI utilise pour tenir compte de la corrélation électronique une fonction d'onde variationnelle qui est une combinaison linéaire de fonctions d'état de configuration (configuration state function - CSF) construite à partir des orbitales de spin (indiquées par l'exposant SO) :
dans laquelle Ψ est généralement l'état essentiel du dispositif. Si le développement inclut l'ensemble des fonctions d'état de configuration de la symétrie appropriée, il existe une démarche de configuration d'interaction complète (CID) qui résout précisément l'équation de Schrödinger électronique dans l'espace défini par la base à une particule. Le premier terme dans le développement ci-dessus est normalement le déterminant Hartree-Fock. Les autres CSF peuvent être déterminées par le nombre d'orbitales de spin échangées avec les orbitales virtuelles du déterminant de Hartree-Fock. Si seule une orbitale de spin change, on la décrit comme une déterminant d'excitation simple. Si deux orbitales changent, elles sont décrites comme un déterminant d'excitation double et ainsi de suite. In procède ainsi pour limiter le nombre de déterminants dans le développement. A titre d'exemple, la méthode CID est limitée à la double excitation uniquement. La méthode CISD est limitée aux excitations simples et doubles. Les excitations simples indépendantes ne se mélangent pas avec le déterminant de Hartree-Fock. Ces méthodes (CID et CISD), sont utilisées par de nombreux programmes standard. La correction de Davidson est parfois utilisée pour estimer une correction de l'énergie CISD pour prendre en compte des excitations d'ordre supérieur. Lors de la résolution des équations CI, les approximations vers les états excités sont aussi obtenues, qui changent par les valeurs de leurs cœfficients cI. La procédure CI conduit à l'la détermination des valeurs propres d'une matrice
où c est le cœfficient du vecteur, e est la matrice des valeurs propres, et les éléments des matrices hamiltonienne et de recouvrement sont , respectivement,
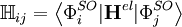 ,
,
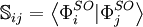 .
.
Les déterminants de Slater sont fabriqués à partir d'ensembles d'orbitales de spin orthonormées, donnant ainsi 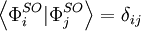 , identifiant
, identifiant 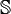 à la matrice identité et simplifiant l'équation matricielle ci-dessus.
à la matrice identité et simplifiant l'équation matricielle ci-dessus.
Voir aussi
- Corrélation électronique
- Interaction de configuration multiréférence
- Méthode post-Hartree-Fock
- Chimie quantique
- (en) Cet article est partiellement ou en totalité issu d'une traduction de l'article de Wikipédia en anglais intitulé «Interaction configuration».
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

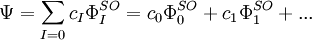
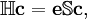

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité