Orbitale de type gaussien
En chimie numérique, les orbitales de type gaussien sont des fonctions utilisées comme orbitales atomiques dans les méthodes LCAO pour le calcul des orbitales électroniques dans les molécules ou les solides.
Recherche sur Google Images :
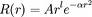
Source image : fr.wikipedia.org Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- des intégrales quand plus de deux atomes sont présents..... par 1 gaussienne, avec des orbitales de polarisation d (p sur les hydrogènes). Ce code est ... explicitement. Plusieurs bases de ce type sont disponibles dans Gaussian. (source : cat.inist)
- auteurs - Dernier message : 18 fév 2005 GTO : Orbitales de Type Gaussienne. c'est une fonction de base dans .... Evalue les intégrales mono électroniques. Deviner les orbitales de ... (source : books.google)
En chimie numérique, les orbitales de type gaussien (connues aussi comme orbitales gaussiennes ou gaussiennes, en anglais Gaussian orbitals - GTO) sont des fonctions utilisées comme orbitales atomiques dans les méthodes LCAO pour le calcul des orbitales électroniques dans les molécules ou les solides.
Utilisation
La raison principale d'utilisation d'une base de fonctions gaussiennes pour des calculs de chimie numérique est le théorème de produit gaussien, qui assure que le produit de deux fonctions gaussiennes centrées sur deux atomes différents est une somme finie de gaussiennes centrées sur un point sur l'axe qui les connecte. De cette façon, les intégrales à quatre centres peuvent être réduites en sommes finies d'intégrales à deux centres, puis après une étape supplémentaire, en sommes finies d'intégrales à un centre. Une accélération de l'ordre de 4 à 5 ordres de grandeurs comparée aux orbitales de Slater est produite en dépit du surcoût qu'entraîne le plus grand nombre de fonctions de base le plus souvent requis pour un calcul gaussien.
Pour des raisons de convenance, de nombreux programmes d'évaluation des intégrales gaussiennes marchent dans une base de gaussiennes cartésiennes, même si des gaussiennes sphériques sont nécessaires : les «contaminants» sont supprimés a posteriori.
Les orbitales atomiques sont de la forme :
Les GTO sont de la forme :
Intégrales moléculaires
Les intégrales moléculaires sur les fonctions gaussiennes cartésiennes furent en premier lieu proposées par Boys[1] en 1950. Depuis lors, de nombreux travaux ont été effectués afin d'accélérer l'évaluation de ces intégrales qui sont la partie la plus lente (limitante) de nombreux calculs en chimie quantique. McMurchie et Davidson (1978) ont introduit des fonctions gaussiennes hermitiennes afin d'utiliser l'avantage des relations différentielles. Pople et Hehre (1978) ont développé une méthode de coordonnées locales. Obara et Saika ont introduit des relations de récurrence efficaces en 1985, ce qui fut suivi par le développement d'autres relations de récurrence importantes. Gill et Pople (1990) ont introduit un algorithme «prisme» qui permet l'utilisation efficace de 20 chemins de calcul différents.
Notes et références
- ↑ S. F. Boys, Proc. R. Soc. London Ser. À 200, 542 (1950)
Liens externes
- (en) Visualisation de l'ensemble des orbitales courantes et non-courantes, de la 1s à la 7g (noter que les parties radiales des expressions données correspondent aux orbitales de Slater plutôt qu'aux gaussiennes; les parties angulaires, et par conséquent leurs formes comme indiquées sur les figures, sont les même que celles des gaussiennes sphériques).
- (en) Cet article est partiellement ou en totalité issu d'une traduction de l'article de Wikipédia en anglais intitulé «Gaussian orbital».
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

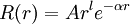
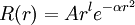

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité