Matrices de Pauli
Les matrices de Pauli, développées par Wolfgang Pauli, forment une base du groupe SU.
Recherche sur Google Images :

Source image : www.ccrs.nrcan.gc.ca Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- Algèbre de Clifford et matrices de Pauli :... linéaire : calcul matriciel, opérateurs linéaires, groupe de rotations, algèbre de Lie, valeurs propres, ... (source : serge.mehl.free)
- ... With the identity matrix {I}, the Pauli matrices form a group. When combined in this way, they are often given the symbols \delta_i... (source : planetmath)
- Pauli matrices - The Pauli matrices are a set of 2 × 2 complex Hermitian and... Pauli matrices, Pauli matrix, Pauli algebra, Pauli operator, Pauli spin... (source : 123exp-math)
Les matrices de Pauli, développées par Wolfgang Pauli, forment une base du groupe SU (2) .
Elles sont définies comme la totalité des matrices complexes de dimensions 2 × 2 suivantes :
(où i est l'unité imaginaire des nombres complexes)
Ces matrices sont fréquemment utilisées en mécanique quantique pour représenter le spin des particules.
Autres propriétés
Le déterminant et la trace des matrices de Pauli sont :
Donc, les valeurs propres de chaque matrice sont 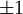 .
.
Les matrices de Pauli obéissent aux relation de commutativité et anticommutativité suivantes :
où εijk est le symbole de Levi-Civita, δij est le delta de Kronecker et I est la matrice identité. Les relations ci-haut peuvent être vérifiées en utilisant :
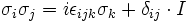 .
.
Ces relations de commutativité sont identiques à celles sur l'algèbre de Lie su (2) et , en effet, su (2) peut être interprétée comme l'argèbre de Lie de l'ensemble des combinaisons linéaires de l'imaginaire i fois les matrices de Pauli iσj, c'est à dire, comme les matrices anti-hermitiennes 2×2 avec trace de 0. Dans ce sens, les matrices de Pauli génèrent su (2). Donc, iσj peut être vu comme les générateurs illimitétésimaux du groupe de Lie correspondant SU (2) .
L'algèbre de su (2) est isomorphe à l'algèbre de Lie so (3), laquelle correspond au groupe de Lie SO (3) , le groupe des rotations en trois dimensions. En d'autres termes, les iσj sont des réalisations de rotations «illimitétésimales» dans un espace à trois dimensions (en fait, ce sont les réalisations qui plus est basse dimension).
Physique
En mécanique quantique les iσj représentent les générateurs des rotations sur les particules non relativistes de spin ½. L'état de ces particules est représenté par des spineurs à deux composantes, ce qui est la représentation principale de SU (2). Une propriété intéressante des particules de spin ½ est qu'elles doivent subir une rotation de 4π radians pour revenir dans leur configuration d'origine. Ceci est dû au fait que SU (2) et SO (3) ne sont pas globablement isomorphes, malgré le fait que leur générateur illimitétésimal, su (2) et so (3), sont isomorphes. SU (2) est en fait une «revêtement de degré deux» de SO (3) : à chaque élément de SO (3) correspondent deux éléments de SU (2).
En mécanique quantique à plusieurs particules, le groupe de Pauli Gn est aussi utile. Il est défini comme l'ensemble des produits tenseurs à n dimensions de matrices de Pauli.
Avec la matrice identité I, quelquefois dénotée σ0, les matrices de Pauli forment une base de l'espace vectoriel réel des matrices hermitiennes complexes 2 × 2. Cette base est équivalente aux quaternions. Quand qu'utilisée comme base pour l'opérateur de rotation de spin ½, est est semblable à celle pour la représentation de rotation de quaternion correspondante.
Voir aussi
- Moment angulaire
- Matrices de Gell-Mann
- Groupe de Poincaré
Référence
- (en) Liboff, Richard L. (2002). Introductory Quantum Mechanics, Addison-Wesley. ISBN 0805387145.
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

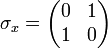
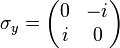
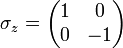
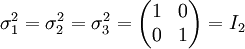
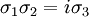
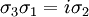
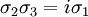
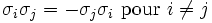
![\begin{matrix}
\det (\sigma_i) &=& -1 & \\[1ex]
\operatorname{Tr} (\sigma_i) &=& 0 &
\end{matrix}\quad \hbox{pour}\ i \in \{1; 2; 3\}](illustrations/7e0ee486e0bce9038088234bdfa211eb.png)
![\begin{matrix}
[\sigma_i, \sigma_j] &=& 2 i\,\epsilon_{i j k}\,\sigma_k \\[1ex]
\{\sigma_i, \sigma_j\} &=& 2 \delta_{i j} \cdot I
\end{matrix}](illustrations/9fafd165ae65074c651460ed1d66e005.png)

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité