Théorie de Mie
En physique optique ondulatoire, la théorie de Mie, aussi nommée théorie de Lorenz-Mie, est une théorie de la diffraction de la lumière par des particules sphériques.
Recherche sur Google Images :

Source image : www.fresnel.fr Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- Pour les faibles niveau de diffusion la théorie de Mie est bien vérifiée et ce... cohérente de la lumière diffusée dans la direction de l'onde incidente.... (source : espci)
- La théorie de Mie est le résultat de la résolution des équations de Maxwell pour l'interaction d'une onde électromagnétique avec des particules dont la... (source : personnel.univ-reunion)
- La théorie de Mie est une expansion de la théorie de . Fraunhofer.... utilisent le principe physique de diffusion des ondes électromagnétiques.... (source : books.google)
En physique optique ondulatoire, la théorie de Mie, aussi nommée théorie de Lorenz-Mie, est une théorie de la diffraction de la lumière par des particules sphériques. Elle tire son nom du physicien danois Ludvig Lorenz et du physicien allemand Gustav Mie, qui lui donna sa première forme en 1908. [1] Elle reçut de nombreux apports par le physicien Peter Debye dans les années qui suivirent.
Diffusion de Rayleigh, cas limite de la diffusion de Mie
La diffusion par des particulièrement petites particules, telles que des molécules, de dimensions inférieures au dixième de la longueur d'onde de la lumière reconnue, est un cas limite nommé diffusion Rayleigh. Pour les particules plus grosses que la longueur d'onde, on doit prendre en compte la diffusion de Mie dans son intégralité : elle explique dans quelles directions la diffusion est la plus intense, on obtient ainsi un «patron de réémission» qui est comparable à celui des lobes d'émission d'une antenne, avec, dans le cas de grosses particules, un lobe plus intense dans la direction opposée à celle d'où provient l'onde incidente.
La diffusion de Mie n'est pas fortement dépendante de la longueur d'onde utilisée comme c'est le cas dans celle de Rayleigh. Elle produit par conséquent une lumière presque blanche quand le Soleil illumine de grosses particules dans l'air : c'est cette dispersion qui donne la couleur blanc laiteux à la brume et au brouillard.
Cependant, si les solutions apportées par la diffusion de Mie sont exactes (pour des sphères), elles ne sont pas toutes analytiques, et on est fréquemment limité à des approches numériques.
Comparaison pratique entre la diffusion de Mie et la diffusion Rayleigh
La diffusion Rayleigh est un cas limite de la diffusion de Mie. Néanmoins, elle change par plusieurs aspects perceptibles quand on les compare pour des particules de tailles particulièrement différentes.
On peut apprécier la différence entre la diffusion Rayleigh et la diffusion Mie en observant le ciel : pour les molécules qui forment l'atmosphère, la première explique la couleur bleue du ciel ; pour les gouttelettes d'eau qui forment les nuages, la seconde explique leur blanc.
La première est fortement dépendante de la longueur d'onde, mais disperse uniformément dans l'ensemble des directions. Dans ce cas, si par exemple le Soleil est à gauche, et l'observateur est à la verticale, c'est le bleu qui reste du spectre solaire à cet angle.
Les gouttelettes du nuage étant particulièrement larges comparé à la lumière visible, la dispersion est celle de Mie : uniforme sur l'ensemble des couleurs du spectre, mais anisotrope, en particulier vers l'avant. L'observateur voit par conséquent en particulier les bordures du nuage en blanc prononcé, puis un dégradé. [2]
Formalisme et résultats
La théorie de Mie étudie le problème par des séries sphériques, c'est-à-dire des sommes illimitées d'harmoniques sphériques. La diffusion de Mie est indépendante de l'intensité lumineuse et de la nature exacte de la particule.
C'est cette sommation illimitée — qu'on ne sait pas forcément exprimer — qui n'a permis l'utilisation pratique de cette méthode qu'au cours des 30 dernières années, d'une part quand les premiers calculateurs électroniques ont pu faire des évaluations numériques, et d'autre part grâce à l'utilisation des séries de Debye qui en donnent une approximation.
La section efficace de diffusion est le rapport entre la puissance électromagnétique diffusée et l'énergie incidente (moyenne temporelle du vecteur de Poynting) On montre que la section efficace de la diffusion de Mie pour une particule sphérique de rayon a pour une onde incidente plane de nombre d'onde k est :
Puisqu'on a, dans le cas général, la relation :
on retrouve la diffusion Rayleigh quand la longueur d'onde est particulièrement supérieure à a : la diffusion est en 1/λ⁴. On observe aussi que, si ce n'est plus le cas, le facteur a est beaucoup dominant et la diffusion est quasiment semblable pour tout le spectre visible — qui est peu étendu.
Si on note θ l'angle constitué par une direction et la direction de l'onde incidente, la diffusion est à symétrie cylindrique d'axe θ = 0 et la section efficace angulaire est :
La diffusion se fait alors essentiellement dans la direction θ = 0, où cette quantité est maximale. L'autre cas limite est la théorie de la diffraction selon ce même axe. La théorie de Mie peut ainsi expliquer certains phénomènes comme les arcs-en-ciel, quoiqu'elle ne soit pas une approche indispensable.
La diffusion de Mie est un problème vectoriel qui implique l'utilisation sous leur forme complète des champs électrique et magnétique. [3]
On se donne une fonction scalaire Ψ qui satisfait l'équation de d'Alembert :
avec n l'indice de réfraction du milieu, k le nombre d'onde et  l'opérateur formel nabla. On pose les vecteurs M et N tels que :
l'opérateur formel nabla. On pose les vecteurs M et N tels que :
avec r le vecteur position. Alors, en coordonnées sphériques, M et N satisfont l'équation de d'Alembert.
La résolution de la diffusion de Mie pour Ψ donne accès aux deux champs vectoriels, desquels on déduit l'onde diffusée.
Résolution et conditions limites
En coordonnées sphériques, il existe des solutions stationnaires à l'équation d'onde. On les exprime en termes d'harmoniques sphériques. Ces solutions sont génèrées par deux fonctions de la forme :
avec N et L deux paramètres entiers, 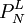 les polynômes de Legendre, zN les fonctions de Bessel sphériques, r, θ et ϕ sont les coordonnées sphériques.
les polynômes de Legendre, zN les fonctions de Bessel sphériques, r, θ et ϕ sont les coordonnées sphériques.
La particule étant de rayon a, la lumière incidente de longueur d'onde λ, on introduit pour simplifier x défini par :
Alors les conditions limites imposent les cœfficients de la solution de la diffusion Mie :
avec Ψ et ζ les fonctions de Riccati-Bessel [4].
La section efficace de la diffusion est donnée par :
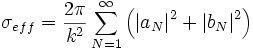 .
. 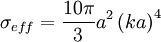
Plasmon de Mie
La diffusion de Mie peut aussi être observée pour des molécules suffisamment grosses, ou des rayonnements suffisamment fins pour que l'objet reste d'une taille importante devant la longueur d'onde. Cependant, on ne peut pas forcément traiter ces cas dans le cadre strict de la théorie de Mie, qui s'applique en toute rigueur à des sphères diélectriques. Il est cependant envisageable de retrouver ses résultats en considérant un modèle (classique) du comportement électronique.
Si on suppose les molécules sphériques, constituées d'un nuage chargé positivement et fixe (le noyau) et d'un nuage chargé négativement et mobile (les électrons), liés seulement par l'attraction électrostatique. C'est le modèle du plasmon de Mie : les mouvements des charges rayonnent une onde électromagnétique.
L'origine de ces mouvements est due à l'absorption d'un photon, qui apporte une impulsion au nuage électronique[5]. Il y a par conséquent absorption puis réémission : c'est bien un phénomène de diffusion.
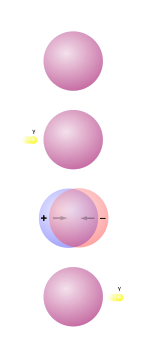
La description du phénomène peut être faite en considérant les mouvements relatifs des «nuages» :
- à l'origine, ils sont confondus, la totalité est neutre ;
- un photon est absorbé par le nuage électronique, qui se déplace ;
- le déplacement des électrons crée un excès de charges, qui attire les nuages l'un vers l'autre ;
- cette accélération génère un rayonnement ;
Il peut se produire plusieurs oscillations, mais l'énergie est progressivement perdue par rayonnement, et le dispositif revient à l'équilibre. Surtout, la diffusion est globalement isotrope.
Le plasmon de Mie est différent des modèles utilisés par la théorie de la diffusion Rayleigh : en effet, cette dernière utilise l'électron élastiquement lié. Dans ce modèle, qui est une approximation des résultats de mécanique quantique à l'ordre 2, la force de rappel exercée sur les électrons est proportionnelle au carré de l'écart x — pour le plasmon de Mie, la force de rappel est proportionnelle à l'inverse du carré de l'écart.
Cette expression implique qu'un photon d'énergie suffisante pourrait séparer le noyau de ses électrons, autrement que par un processus d'ionisation, ce qui n'est pas acceptable physiquement : le modèle du plasmon de Mie n'est valable que pour des longueurs d'onde suffisamment larges.
Notes et références
- ↑ (de) Gustav Mie, «Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen». Ann. Phys. Leipzig 25, 377–445 (1908) ;
- ↑ (de) «Grundlagen der atmosphärischen Optik».
- ↑ Il est aussi envisageable d'étudier le problème par d'autres méthodes, voir par exemple (de) «Mie-Streuung und Lokalisierung».
- ↑ (pl) «Wykład 3. Rozpraszanie promieniowania»
- ↑ Quoique ce modèle utilise l'énergie du photon, résultat quantique lié à la constante de Planck, le plasmon de Mie n'utilise que des arguments de mécanique classique.
- (en) Animations de la diffusion Mie pour différentes particules ;
- (en) Calculateur en ligne de la diffusion Mie ;
- (en) ScatLab propose un logiciel de simulation de la diffusion ;
- (en) Implémentations de la diffusion Mie en C, C++, Fortran, Matlab et Mathematica ;
Bibliographie
- (en) A. Stratton, Electromagnetic Theory. McGraw-Hill, New York, 1941 ;
- (en) H. C. van de Hulst, Light scattering by small particles. Dover, New York, 1981 ;
- (en) M. Kerker, The scattering of light and other electromagnetic radiation. Academic, New York, 1969 ;
- (en) C. F. Bohren, D. R. Huffmann, Absorption and scattering of light by small particles. Wiley-Interscience, New York, 1983 ;
- (en) P. W. Barber, S. S. Hill, Light scattering by particles : Computational Methods. World Scientific, Singapour, 1990 ;
- (en) Hong Du, «Mie-scattering calculation», Applied Optics 43 (9), 1951-1956 (2004).
- (en) Thomas Wriedt, «Mie theory 1908, on the mobile phone 2008», Journal of Quantitative Spectroscopy & Radiative Transfer 109, 1543–1548 (2008).
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.



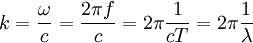
![\frac{d \sigma_{eff}}{d \Omega} \left( \theta \right) = aˆ2 \left( ak \right)ˆ4 \left[ \frac{5}{8} \left( 1 + \cosˆ2 \theta \right) + \cos{\theta} \right]](illustrations/c1735b5b899536678d237d897badd3b3.png)
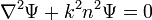
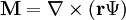
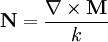
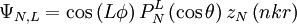
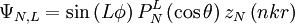
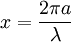
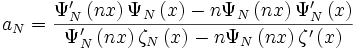
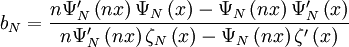

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité