Calculateur quantique
Un calculateur quantique ou ordinateur quantique, repose sur des propriétés quantiques de la matière : superposition et intrication d'états quantiques.

Catégories :
Architecture informatique - Physique quantique - Informatique quantique - Mécanique quantique
Recherche sur Google Images :

Source image : www.cemes.fr Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- "Il est ainsi facile de calculer qu'un ordinateur quantique de 300 qbits pourraient gérer à peu près 1090 informations, soit plus que le nombre d'atomes dans ... (source : presence-pc)
- Le calcul quantique sert à calculer précisément les mêmes fonctions qu'un ordinateur classique. Par conséquent l'ensemble des algorithmes classiques peuvent exister en ... (source : griffonnages)
Un calculateur quantique ou ordinateur[1] quantique, repose sur des propriétés quantiques de la matière : superposition et intrication d'états quantiques. De petits calculateurs quantiques ont déjà été fabriqués dès les années 1990 et des progrès sont en cours. Ce domaine en essor est soutenu financièrement par plusieurs organisations, entreprises ou gouvernements, du fait de l'importance de l'enjeu : au moins un algorithme conçu pour utiliser un circuit quantique, l'algorithme de Shor, rendrait envisageable de nombreux calculs combinatoires[2] hors de portée d'un ordinateur classique en l'état actuel des connaissances. La possibilité de casser les méthodes cryptographiques classiques est fréquemment mise en avant. La difficulté actuelle majeure (depuis 2008) concerne la réalisation physique de l'élément de base de l'ordinateur quantique : le qubit. Le phénomène de décohérence, c'est-à-dire de perte des effets quantiques sur le long terme, est le principal frein au développement de l'ordinateur quantique.
Intérêt des ordinateurs quantiques
Si de grands (plus de 300 qubits) ordinateurs quantiques pouvaient être fabriqués — ce qui n'est pas assuré — ils seraient capables selon David Deutsch[3] de simuler le comportement de l'univers lui-même. Ils pourraient aussi résoudre des problèmes de cryptanalyse en un temps polynomial et non exponentiel comme un ordinateur classique. Les ordinateurs quantiques font appel à des techniques de calcul complètement différentes de celles généralement connues. Ils se basent sur des propriétés quantiques de la matière. De nombreux dispositifs (transistors des ordinateurs classiques, afficheurs LCD, imprimantes à laser... ) exploitent certes des effets quantiques dans leur fonctionnement, mais représentent l'information sous forme de bits classiques. Un calculateur quantique utilise au contraire des qubits (bits quantiques) contenant plusieurs informations intriquées. Un algorithme dû à Peter Shor permet d'utiliser un calculateur quantique pour "casser" le code RSA. Cette découverte a stimulé la recherche sur le sujet.
Des moyens de chiffrement quantique existent aussi dans le commerce. Ils ne demandent pas de calculateur quantique, mais demandent une mise en place plus complexe qu'un cryptage standard.
Que des calculateurs quantiques de taille intéressante soient envisageables ou non à terme, leur premier avenir commercial ne sera certainement pas dans le grand public : le calcul quantique exige peu d'entrées et peu de sorties. Il ne se prête par conséquent a priori qu'aux calculs dont la complexité réside dans la combinatoire. On trouve ces problèmes dans l'ordonnancement et autres calculs de recherche opérationnelle, en bio-informatique, et évidemment en cryptographie.
Algorithmes utilisant des circuits quantiques
Comme vu plus haut, c'est la combinatoire qui forme le champ de travail privilégié des futures cartes de calcul quantique, si elles existent un jour.
Ainsi il peut être particulièrement complexe de trouver l'ensemble des facteurs premiers d'un grand nombre (par exemple de 1000 chiffres). Ce problème de factorisation est complexe pour un ordinateur ordinaire à cause de l'explosion combinatoire. Un circuit de calcul quantique pourrait résoudre ce problème en un temps polynomial, c'est-à-dire que pour l'ordinateur quantique, la difficulté augmenterait polynomialement au lieu d'augmenter exponentiellement.
Une ressemblance envisageable est de se représenter un calculateur quantique comme un processeur SIMD (carte graphique, par exemple) dont le nombre de pipelines soit 2N fois le nombre de qubits. L'ressemblance s'arrête là, un calculateur quantique ne pouvant apporter qu'un bit de résultat à la fois (l'état quantique étant détruit par l'observation), après quoi le calcul doit être recommencé pour demander le suivant.
Cette capacité permettrait à un ordinateur quantique de casser une bonne partie des dispositifs cryptographiques aujourd'hui utilisés, surtout la majorité des méthodes de chiffrement asymétriques : RSA, ElGamal ou Diffie-Hellman. Ces algorithmes sont utilisés pour protéger des pages Web, des messages électroniques, et énormément d'autres types de données. Parvenir à passer ces protections serait un avantage majeur pour l'organisation ou le pays qui y parviendrait, et une réédition de l'exploit réalisé pour Enigma.
La seule façon de rendre sûr un algorithme tel que RSA serait d'augmenter la taille de la clé (et par conséquent la lenteur du codage) jusqu'à ce qu'elle soit plus grande que le plus grand des circuits de calcul quantique existants. Or la taille des moyens de calcul dont dispose par exemple la National Security Agency ne sera bien entendu jamais rendue publique. La conséquence en est que les pays ou organismes voulant se protéger verront augmenter de plusieurs ordres de grandeur le coût et le délai de leurs communications, sans jamais être certains pour tout autant que cela serve à quelque chose. Si le RSA peut par conséquent être rendu sûr, ce sera malheureusement au prix d'une lourde réorganisation des communications, de leur coût, et de leur commodité. Ou alors il faudra inventer de nouveaux algorithmes de chiffrement capables de rivaliser avec le calcul quantique.
Des circuits quantiques sont déjà utilisés pour des simulations de mécanique quantique. C'est pourquoi Richard Feynman les avait imaginés au départ. Ils sont aussi particulièrement utiles, car les calculs quantiques deviennent complexes dès qu'on sort de quelques cas triviaux.
Un autre algorithme, quoique de gain moins spectaculaire, a été découvert ensuite : la recherche quantique rapide dans une base de données (en anglais : quantum database search) par l'algorithme de Grover[4]. Au lieu de parcourir l'ensemble des éléments d'une liste pour trouver celui qui répond le mieux à un critère (par exemple : recherche d'une personne dans l'annuaire pour trouver son numéro de téléphone), cet algorithme utilise des propriétés de superposition pour que la recherche se fasse de façon globale. Les résultats devraient être en 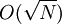 , N étant le nombre de fiches (et O représentant la comparaison asymptotique), soit mieux qu'une base de données classique bien optimisée, sous réserve de disposer d'un registre quantique de taille suffisante pour les calculs. Curieusement, le procédé rappelle dans son principe celui des anciennes fiches à tringles permettant d'accéder directement aux informations recherchées.
, N étant le nombre de fiches (et O représentant la comparaison asymptotique), soit mieux qu'une base de données classique bien optimisée, sous réserve de disposer d'un registre quantique de taille suffisante pour les calculs. Curieusement, le procédé rappelle dans son principe celui des anciennes fiches à tringles permettant d'accéder directement aux informations recherchées.
Des circuits de calcul quantique apportent par conséquent un plus aux ordinateurs classiques dans quatre types d'applications :
- la décomposition en produit de facteurs premiers ;
- le logarithme discret ;
- les simulations de physique quantique.
Historique
Dans les années 1970 et 80, les premiers ordinateurs quantiques naissent par retournement dans l'esprit de physiciens tels que Richard Feynman, Paul Benioff, David Deutsch ou Charles H. Bennett. L'idée de Feynman était : «Au lieu de nous plaindre que la simulation des phénomènes quantiques demande des puissances énormes à nos ordinateurs actuels, utilisons la puissance de calcul des phénomènes quantiques pour faire plus puissant que nos ordinateurs actuels».
Longtemps les physiciens ont douté que les ordinateurs quantiques utilisables puissent exister, et même qu'on puisse en faire quelque chose de viable s'ils existaient. Mais :
- en 1994, Peter Shor, chercheur chez AT&T, montre qu'il est envisageable de factoriser des grands nombres dans un temps raisonnable avec un ordinateur quantique. Cette découverte débloque brusquement des crédits ;
- en 1996, Lov Grover (en) [5], invente un algorithme basé sur les ordinateurs quantiques servant à trouver une entrée dans une base de données non triée en
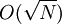 (voir : complexité algorithmique) ;
(voir : complexité algorithmique) ; - en 1998, IBM est le premier à présenter un ordinateur quantique de 2 qubits ;
- en 1999, l'équipe d'IBM utilise l'algorithme de Grover sur un calculateur de 3 qubits et battent leur record l'année suivante avec un ordinateur de 5 qubits ;
- le 19 décembre 2001, IBM crée un ordinateur quantique de 7 qubits et factorise le nombre 15[6] grâce à l'algorithme de Shor. Ces ordinateurs à 7 qubits sont bâtis autour de molécules de chloroforme et leur durée de vie utile ne dépasse pas quelques minutes. On parle par dérision de wetware.
- 2006 :
- Seth Lloyd, professeur au Massachusetts Institute of Technology (MIT), pionnier du calcul quantique et auteur du livre Hacking the universe, mentionne dans le numéro d'août 2006 de la revue Technology Review (page 24) l'existence d'ordinateurs quantiques à 12 qubits.
- L'institut de traitement de l'information quantique de l'université d'Ulm en Allemagne présente en avril 2006 la première micropuce européenne linéaire tridimensionnelle qui piège plusieurs atomes ionisés Ca+ de manière isolée.
- 2007
La controverse D-Wave
La société D-Wave a annoncé officiellement le 13 février 2007[7] avoir réalisé un ordinateur quantique à base solide de 16 qubits[8]. Ce calculateur serait cependant limité à certaines opérations quantiques. Aucun prototype n'a été dûment testé par des spécialistes reconnus des ordinateurs quantiques, pour des raisons alléguées de secret industriel (le prototype n'était pas présent durant la conférence). Ces machines utiliseraient une puce appelée Europa qui fonctionne seulement en milieu cryogénique. Reflétant le sentiment d'une partie de la communauté scientifique, Scientific American reste réservé[9]. Les problèmes combinatoires résolus (Sudoku) le sont moins vite qu'avec un simple ordinateur. Il n'y a là rien d'étonnant au vu des caractéristiques de l'appareil, mais donc on ne peut exclure complètement une opération du type Turc mécanique ayant simplement pour objectif de lever des fonds, d'autant que D-Wave promet un ordinateur quantique à 32 qubits pour la fin de l'année, et un ordinateur à 512 puis à 1024 qubits d'ici l'année prochaine[10].
En décembre 2007 et selon le site même du constructeur, les seules nouvelles concernant D-wave depuis février auront été sa participation à une conférence sur le calcul massif[11] et la démonstration alléguée d'une machine à 28 qubits[12] en novembre, commentée en détail par Tom's Hardware[13] en juillet 2008. La compagnie a affirmé maintenir ses objectifs de 512 qubits au second trimestre 2008 et 1024 qubits fin 2008, et assuré que la commercialisation des calculateurs quantiques était bien "une question d'années et non de décennies"; elle a mentionné aussi son intention de rendre son calculateur et les capacités de corrélation particulièrement rapides de ce dernier accessibles à des chercheurs via l'Internet (Tom's Hardware). Début décembre 2008, on constate que le site de la compagnie ne donne plus de nouvelles depuis la fin de sa levée de fonds.
Réalisations physiques
Un ordinateur quantique pourrait être implémenté à partir de toute particule pouvant avoir deux états à la fois excités et non excités au même moment. Ils peuvent être fabriqués à partir de photons présents à deux lieux au même moment, ou à partir de protons et de neutrons ayant un spin positif, négatif ou les deux en même temps tant qu'ils ne sont pas observés.
Contraintes physiques
Une molécule microscopique pouvant contenir plusieurs millions de protons et de neutrons, on pourrait imaginer de les utiliser comme ordinateurs quantiques avec plusieurs millions de qubits, mais le calcul quantique exige du dispositif qui le porte deux contraintes fortes pour être utilisable :
- il doit être complètement isolé du monde extérieur au cours de la phase calcul, toute observation perturbant le processus. On ne le laisse communiquer à l'extérieur qu'avant (introduction des données) et après (lecture des résultats, ou plus précisément du résultat) ; l'isolement thermique total ne peut exister, mais si on arrive à le maintenir le temps du calcul, ce dernier peut avoir lieu sans interférence. Ce phénomène d'interférence est nommé décohérence, c'est le principal obstacle à la réalisation d'ordinateur quantique. Le temps de décohérence correspond pour un dispositif quantique au temps pendant lequel ses propriétés quantiques ne sont pas corrompues par l'environnement.
- il doit se faire sans la moindre perte d'information. Surtout tout circuit de calcul quantique doit être réversible. Dans les circuits logiques "classiques" certaines portes ne vérifient pas cette propriété (porte NAND par exemple). Cependant des astuces de construction permettent de contourner cette difficulté en conservant des informations supplémentaires non directement utiles. L'ensemble des portes classiques ont un équivalent quantique.
Il existe des dispositifs quantiques isolés naturellement comme les noyaux de certains atomes. Certains, comme le carbone 13, possèdent un moment cinétique, un spin, et peuvent donner lieu à différents états quantiques. Les cristaux de diamant qui contiennent des isotopes du carbone 12 (les noyaux du diamant sont composés jusqu'à 1 % de noyaux de carbone 13) permettraient théoriquement à température ambiante de stocker et de manipuler de l'information quantique. Une première technique consiste à manipuler par laser le spin des électrons d'un atome d'azote constituant les impuretés du diamant, et ainsi agir sur le couplage entre le spin de ces électrons et celui des noyaux du carbone 13[14].
Projets en cours
De nombreux projets sont en cours à travers le monde pour construire concrètement des qubits viables et les réunir dans un circuit. Ces recherches mettent en œuvre de la physique théorique pointue. Les projets suivants semblent avancer à un rythme intéressant :
- les circuits supraconducteurs avec jonction Josephson. Cette technique est particulièrement malléable : il s'agit de dessiner des circuits suffisamment résistants à la décohérence. Pour le moment elle ne sert à coupler qu'au plus deux qubits, mais des recherches sont en cours pour en coupler davantage avec un résonateur et d'un SQUID.
- Les ions piégés. Cette technique a donné le dispositif possédant le plus de qubits intriqués.
- la Résonance magnétique nucléaire.
- les atomes provenant d'un condensat de Bose-Einstein piégés dans un réseau optique.
- les cavités optiques ou micro-ondes résonantes.
- les boîtes quantiques (quantum dots en anglais) : ce sont des dispositifs macroscopiques qui possèdent malgré tout les caractéristiques quantiques nécessaires pour l'élaboration d'un ordinateur quantique. On nomme quelquefois de tels dispositifs des atomes artificiels. Cette technique utilise des matériaux courants dans l'industrie des semi-conducteurs : silicium ou arséniure de gallium. Elle se subdivise en deux branches : l'une exploitant la charge électrique des qubits, l'autre leur spin (voir l'article spintronique).
- énormément d'autres projets plus ou moins avancés.
Certains projets semblent particulièrement en phase avec une exploitation industrielle, mais les problèmes de base restent les mêmes. Des recherches sont ainsi entreprises pour réaliser un ordinateur quantique à base solide, comme le sont nos microprocesseurs actuels. Ces recherches ont entre autres mené l'Université du Michigan à une puce de calcul quantique capable d'être fabriquée en série, sur les lignes de productions existant aujourd'hui. Qui plus est , cette puce permet en effet d'isoler un ion et de le faire «léviter» dans un espace confiné, au sein de la puce.
Principe de fonctionnement des ordinateurs quantiques
Le fonctionnement des ordinateurs quantiques peut paraître mystérieux au premier abord : la théorie quantique est une théorie décrivant des probabilités de présence. Comment par conséquent concilier ce concept d'aléa avec un calcul qui se veut déterministe ?
Idées de la mécanique quantique
En réalité, les fonctions d'onde, c'est-à-dire les distributions de probabilité de présence à la base de la théorie quantique, sont issues de calculs tout ce qu'il y a qui plus est déterministes. La source d'aléa est dans l'acte d'observation lui-même, c'est-à-dire la mesure. En effet, suite à une mesure, le dispositif quantique se fixe dans un état avec une certaine probabilité. On peut contourner cette incertitude en la rendant la plus faible envisageable par un jeu d'opérations quantiques successives. Pour certains algorithmes, il peut être indispensable d'effectuer les calculs plusieurs fois jusqu'à ce que la réponse vérifie une certaine propriété.
En mécanique quantique, il est envisageable pour une particule d'être dans de multiples états simultanément. Cette possibilité est nommée superposition. Pour décrire ce phénomène, on parle quelquefois du paradoxe du chat de Schrödinger qui est , pour l'observateur, à la fois mort et/ou vivant. Quand le chat dort, il est immobile, et on ne peut pas dire en le regardant s'il dort ou s'il est mort. Le chat peut par conséquent être dans deux états différents qu'on ne peut différencier seulement par l'observation.
- L'observateur qui veut étudier avec une certitude absolue l'état de mort du chat ne pourra s'assurer qu'il est bien mort qu'en essayant de le réveiller. Si le chat est bien mort, le chat ne se réveille pas, par conséquent ne change pas de position, par conséquent l'état n'est pas perturbé, et on peut étudier cet état de mort du chat en étant certain que le chat qu'on observe est bel et bien mort.
- Mais l'observateur qui veut étudier avec une certitude absolue l'état de sommeil du chat ne pourra s'assurer de cet état qu'en réveillant le chat. C'est ici qu'est le paradoxe : en réveillant le chat, l'observateur altère l'état qu'il voulait étudier, et il ne peut par conséquent plus l'étudier. L'astuce consiste par conséquent à supposer que le chat est endormi (probabilité = 50% = 1 chance sur 2), à l'observer en premier lieu, puis à vérifier ensuite en essayant de le réveiller. On ne conserve les résultats de l'observation que si le chat se réveille.
- Avec uniquement 2 états envisageables, le raisonnement est simple. Tout se complique si on considère qu'il y a plusieurs chats à étudier en même temps et qu'il y a 3 états envisageables, c'est-à-dire que chaque chat peut être soit mort, soit endormi, ou bien les 2 états à la fois en superposition (ce qui est envisageable pour une particule isolée).
Cependant au niveau quantique, il ne s'agit pas uniquement d'un modèle servant à rendre compte de notre ignorance du dispositif. Les particules sont véritablement dans cet état juxtaposé, et il en découle un certain nombre de propriétés inédites à notre échelle. Une mesure sur un dispositif quantique va le forcer à choisir un des états. On parle de projection.
Le qubit
La mémoire d'un ordinateur classique est faite de bits. Chaque bit porte soit un 1 soit un 0. La machine calcule en manipulant ces bits. Un ordinateur quantique travaille sur un jeu de qubits. Un qubit peut porter soit un un, soit un zéro, soit une superposition d'un un et d'un zéro (ou, plus précisément, il porte une distribution de phase, angle qui pour 0° lui fait prendre la valeur 1, pour 90° la valeur 0, et entre les deux la superposition d'états dans les proportions du sin² et du cos² de la phase). L'ordinateur quantique calcule en manipulant ces distributions. On n'a par conséquent pas trois états en tout mais une illimitété.
De plus, l'état de plusieurs qubits réunis n'est pas uniquement une combinaison des états respectifs des qubits. En effet, si un qubit est dans une quelconque superposition d'états 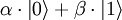 , deux qubits réunis sont quant à eux dans une superposition d'états
, deux qubits réunis sont quant à eux dans une superposition d'états 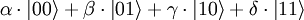 , avec | α | 2 + | β | 2 + | γ | 2 + | δ | 2 = 1. Il s'agit cette fois d'employer la superposition des quatre états pour le calcul. C'est pourquoi la puissance de calcul théorique d'un ordinateur quantique double à chaque fois qu'on lui adjoint un qubit. Avec 10 qubits, on a 1024 états superposables, et avec n qubits, 2n.
, avec | α | 2 + | β | 2 + | γ | 2 + | δ | 2 = 1. Il s'agit cette fois d'employer la superposition des quatre états pour le calcul. C'est pourquoi la puissance de calcul théorique d'un ordinateur quantique double à chaque fois qu'on lui adjoint un qubit. Avec 10 qubits, on a 1024 états superposables, et avec n qubits, 2n.
Un ordinateur classique ayant trois bits de mémoire peut stocker seulement trois nombres binaires. À un moment donné, il pourrait contenir les bits «101» ou une autre combinaison des 8 envisageables (23). Un ordinateur quantique ayant trois qubits peut en fait stocker 16 valeurs, assemblées deux par deux pour former 8 nombres complexes (il est par conséquent dans une superposition de ces 8 états). Il pourrait contenir ceci :
| État | Amplitude | Probabilité |
|---|---|---|
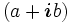 |
(a2 + b2) | |
| 000 | 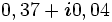 |
0, 14 |
| 001 | 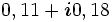 |
0, 04 |
| 010 | 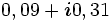 |
0, 10 |
| 011 | 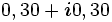 |
0, 18 |
| 100 | 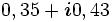 |
0, 31 |
| 101 | 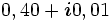 |
0, 16 |
| 110 | 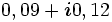 |
0, 02 |
| 111 | 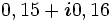 |
0, 05 |
Noter que la somme des probabilités fait bien 1. S'il y avait eu n qubits, cette table aurait eu 2n lignes. Pour un n aux alentours de 300, il y aurait eu plus de lignes que d'atomes dans l'univers observable.
La première colonne montre l'ensemble des états envisageables pour trois bits. Un ordinateur classique peut uniquement porter un de ces états à la fois. Un ordinateur quantique, lui, peut être dans une superposition de ces 8 états à la fois. La seconde colonne montre l'amplitude pour chacun des 8 états. Ces 8 nombres complexes sont un instantané du contenu d'un ordinateur quantique à un moment donné. Durant le calcul, ces trois nombres changeront et interagiront les uns avec les autres. En ce sens, un ordinateur quantique à trois qubits a énormément plus de mémoire qu'un ordinateur classique à trois bits.
Cependant, il n'est pas envisageable de voir directement ces trois nombres. Lorsque l'algorithme est fini, une seule mesure est accomplie. La mesure retourne une simple chaîne de 3 bits classiques et efface les 8 nombres quantiques. La chaîne de retour est générée aléatoirement. La troisième colonne donne la probabilité pour chacune des chaînes envisageables. Dans cet exemple, il y a 14% de chance que la chaîne retournée soit «000», 4% que ce soit «001», ainsi de suite. Chaque nombre complexe est appelé «ampere» et chaque probabilité une «amplitude carrée», parce qu'elle est identique à 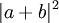 . La somme des huit probabilités est identique à un.
. La somme des huit probabilités est identique à un.
Typiquement, un algorithme d'un ordinateur quantique initialisera l'ensemble des nombres complexes à des valeurs identiques, par conséquent l'ensemble des états auront les mêmes probabilités. La liste des nombres complexes peut être imaginée comme un vecteur à 8 éléments. À chaque étape de l'algorithme, le vecteur est modifié par son produit avec une matrice qui correspond à une opération quantique.
Technologies
Un article publié en avril 2008 par Scientific American fait état d'une avancée[15] vers le calculateur quantique utilisant l'effet Hall quantique fractionnaire.
Simulation d'un ordinateur quantique
Damian Conway a créé pour le langage Perl un module appelé Quantum : :Superpositions[16] qui sert à simuler (en faisant de l'algorithmique ordinaire en coulisses, évidemment) le fonctionnement d'un périphérique de calcul quantique. Ce module est utilisable pour écrire et tester, en version maquette à quelques qubits simulés, des programmes rédigés pour la logique quantique. Les programmes réalisés seront totalement utilisables sur un périphérique de calcul quantique (s'il en existe un jour) en remplaçant les appels au module par les appels correspondant à ce périphérique, sans toucher en rien au programme Perl lui-même excepté en ce qui concerne le nombre de qubits spécifié. On pourra alors tirer parti des capacités d'un ordinateur quantique et effectuer ainsi des calculs plus complexes à temps identique.
Le module munit Perl de deux fonctions testant globalement les tableaux : any () et all () . Dans la simulation, ces fonctions travaillent par itération sur les éléments et par conséquent en un temps O (N). Dans un calcul quantique, leur temps d'exécution serait indépendant de N.
L'expression d'un calcul de primalité :
sub is_prime {
my ($n) = @_;
return $n % all(2..sqrt($n)+1) != 0
}
n'est pas sans rappeler l'écriture en langage APL, qui lui aussi traite globalement les tableaux, ou d'un langage fonctionnel comme Haskell.
Avenir commercial ?
Même si les problèmes techniques posés par la réalisation de calculateurs quantiques sont résolus à terme, leur avenir commercial immédiat ne se situe pas obligatoirement dans le grand public, tout dépendant bien entendu du coût auquel on arrive à les fabriquer.
En dehors des algorithmes de Shor pour le cassage de code et de Grover pour la recherche efficace dans des bases de données, ainsi qu'une classe de calculs en physique théorique, quelques applications seraient peut-être envisageables pour des simulations numériques qui butent actuellement sur l'explosion combinatoire.
En novembre 2008, Aram W. Harrow, Avinatan Hassidim et Seth Lloyd ont publié[17] une méthode quantique servant à résoudre des dispositifs d'équations linéaires à matrices creuses en un temps O (log (n) ) au lieu de O (n).
Quelques autres pistes envisageables :
- Intelligence artificielle pour le traitement automatique des langues (TAL) : en utilisant de grosses ressources combinatoires un traitement de texte pourrait-il utiliser une représentation de l'univers associé à un texte et mieux réagir à la sémantique qu'il pourrait en inférer ?[18].
- À la limite, les amateurs de jeux vidéo seraient-ils heureux de disposer d'un moteur de gestion de collisions physiques particulièrement réaliste ?
- Les traders, ou alors de simples spécifiques porteurs d'actions pourraient-ils envisager un nombre beaucoup plus grand de simulations ?
Généralement l'ensemble des domaines qui peuvent profiter d'une simulation d'un univers riche peuvent théoriquement bénéficier de processeurs quantiques.
Des questions envisagées dans la littérature sont les suivantes : faut-il construire le modèle sur l'ordinateur «classique» puis le faire évaluer par le calculateur quantique, ou bien faut-il laisser tout le travail au calculateur quantique (qui risque d'être moins rapide pour les tâches respectant les traditions) ? [19] Des émulateurs de modèles quantiques ont été fabriqués pour enrichir le débat (cf section sur l'exemple en Perl. ).
En évitant de rééditer quelques erreurs historiques célèbres, bornons-nous à constater que l'avenir reste ouvert en ce qui concerne le calcul quantique chez les particuliers.
Bibliographie
- (en) M. A. Nielsen et Isaac Chuang, "Quantum Computation and Quantum Information", Cambridge University Press, 2000, ISBN 0521635039
- (fr) Michel Le Bellac, "Introduction à l'information quantique", Éditions Belin, 2005, ISBN 2701140323
- (fr) Jean-Baptiste Waldner, "Nano-informatique et intelligence quantique - Inventer l'ordinateur du XXIe siècle", Hermes Science, London, 2006, ISBN 2746215160
Voir aussi
- Algorithme de Shor
- Algorithme de Grover
- Algorithme de Deutsch
- Informatique quantique
- Information quantique
Références
- ↑ Appellation moins appropriée, dans la mesure où il s'agit d'un procédé de calcul sans aucun rapport avec une machine de Von Neumann
- ↑ autrement dit surtout comportant peu d'entrées-sorties comparé au traitement
- ↑ The Fabric of Reality, p. 194 et suivantes
- ↑ P. Arrighi - Homepage
- ↑ Lov K. Grover, «Quantum Computing — How the weird logic of the subatomic world could make it envisageable for machines to calculate millions of times faster than they do today». Consulté le 25 décembre 2008
- ↑ Experimental realization of Shor's quantum factoring algorithm using nuclear magnetic resonance. Consulté le 25 décembre 2008
- ↑ D-Wave Systems News
- ↑ TechWorld News
- ↑ Article du Scientific American
- ↑ Voir article paru dans Automates Intelligents
- ↑ D-Wave Systems : News
- ↑ D-Wave Systems : News
- ↑ http ://www. tomshardware. com/reviews/super-cooled-quantum-computing, 1976. html
- ↑ La mémoire quantique du diamant
- ↑ Scientific American, 21 avril 2008 : Quarter Electrons May Enable Exotic Quantum Computer
- ↑ Le module rédigé initialement par Damian Conway
- ↑ http ://arxiv. org/abs/0811.3171
- ↑ Phd-thesis, Quantum Computation and Natural Language Processing (2002), Joseph C. H. Chen
- ↑ http ://www. mathstat. dal. ca/∼selinger/qpl2006/ 4th Mondial Workshop on Quantum Programming Languages (Regardez à'Quantum arrows in Haskell'de J. K. Vizzotto, A. C. da Rocha Costa, A. Sabry; pour une mise en évidence d'équivalences)
Liens externes
- (fr) Ordinateur quantique, dossier Futura-Sciences
- (fr) Présentation PDF de Frédéric Magniez (CNRS)
- (en) Le site d'IBM sur le calcul quantique
- (en) Introduction à l'informatique quantique, pour les non-physiciens, Michel Le Bellac (CNRS)
- (fr) Introduction à l'informatique quantique sans équations, Alexandre Blais (Yale)
- (en) Page de David Deutsch
- (en) Bases d'algèbre linéaire pour le calcul quantique (PDF)
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 12/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité