Entropie de Rényi
L'entropie de Rényi, due à Alfréd Rényi, est une fonction mathématique qui correspond à la quantité d'information contenue dans la probabilité de collision d'une variable aléatoire.
Catégories :
Théorie de l'information - Informatique quantique - Mécanique quantique - Physique quantique
Recherche sur Google Images :
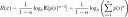
Source image : fr.wikipedia.org Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- paper we introduce the notion of relative Renyi entropy for two...... inequalities and applications to nonlinear diffusions, ” J. Math. Pures... (source : math.poly)
- ) Univ. Toulon Var, dép. mathématiques, PHYMAT, 83957 La Garde, FRANCE... Méthode analytique ; Entropie Rényi ; Transformation ondelette ;... (source : cat.inist)
L'entropie de Rényi, due à Alfréd Rényi, est une fonction mathématique qui correspond à la quantité d'information contenue dans la probabilité de collision d'une variable aléatoire.
Définition formelle
L'entropie de Rényi d'une variable aléatoire discrète x, avec états envisageables 1.. n comme :
![R(x)= \frac{1}{1-\alpha}\log_2{\mathbf E [p(i)ˆ{\alpha-1}]} = \frac{1}{1-\alpha}\log_2 \left( \sum_{i=1}ˆnp(i)ˆ\alpha \right)](illustrations/16512950127b8adeafcf32c6a6c01536.png)
où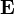 
dénote l'espérance mathématique, α > 0 et 
.
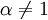Voir aussi
- (en) A. Rényi, On measures of entropy and information, in Proc. 4th Berkeley Symposium on Mathematical Statistics and Probability. vol. 1, 1961, p. 547-561.
Recherche sur Amazone (livres) : |
Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Entropie_de_R%C3%A9nyi.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 12/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 12/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.
Accueil
Recherche
Début page
Contact
Imprimer
Accessibilité