Effet Josephson
En physique, l'effet Josephson se manifeste par la naissance d'un courant entre deux matériaux supraconducteurs scindés par une couche faite d'un matériau isolant ou métallique non-supraconducteur.
Recherche sur Google Images :

Source image : iramis.cea.fr Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- Actuellement l'effet Josephson est utilisé dans de nombreux Instituts Nationaux de ... une jonction Josephson à une température de 4 K pour la... (source : metas)
- Josephson tunnel (jonction SIS) ce courant non dissipatif fluctue comme le sinus de ... Nous proposons d'étudier comment l'effet Josephson est affecté par le ... (source : books.google)
- La preuve usuelle d'un effet Josephson est la présence de marches dans la... On doit noter que la théorie suppose que la jonction est tenue à une... (source : freepatentsonline)
En physique, l'effet Josephson[1]se manifeste par la naissance d'un courant entre deux matériaux supraconducteurs scindés par une couche faite d'un matériau isolant ou métallique non-supraconducteur.
Dans le premier cas, on parle de «jonction Josephson S-I-S» (supraconducteur-isolant-supraconducteur) et dans le second de «jonction S-M-S».
On peut distinguer qui plus est deux types d'effet Josephson [2], l'effet Josephson «continu» (D. C. Josephson effect en anglais) et l'effet Josephson «alternatif» (A. C. Josephson effect). Ces deux effets ont été prédits par Brian David Josephson en 1962 à partir de la théorie BCS. Ces travaux lui ont valu le prix Nobel de physique en 1973, avec Leo Esaki et Ivar Giæver.
Bien que les paires de Cooper ne puissent pas exister dans un isolant ou un métal non-supraconducteur, si la couche qui sépare les deux supraconducteurs est suffisamment mince, elles peuvent la traverser par effet tunnel et garder leur cohérence de phase. C'est la persistance de cette cohérence de phase qui donne lieu à l'effet Josephson.
Effet Josephson alternatif
À cause de l'effet tunnel des paires de Cooper, le courant supraconducteur à travers la barrière séparant les supraconducteurs est :
où Ic est un courant caractéristique de la jonction et φ1, 2 sont les phases supraconductrices des deux supraconducteurs.
D'autre part, la phase supraconductrice étant canoniquement conjuguée avec le nombre de particules, elle obéit à l'équation du mouvement :
où e est la charge de l'électron, et V1 - V2 est la différence de potentiel existant entre les deux supraconducteurs. Il en résulte que :
C'est à dire, l'application d'une différence de potentiel entraîne des oscillations du courant supraconducteur à une pulsation 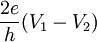 . L'effet Josephson alternatif apporte ainsi un moyen de mesurer le rapport e / h ou de relier les standards du Volt et de la Seconde[3].
. L'effet Josephson alternatif apporte ainsi un moyen de mesurer le rapport e / h ou de relier les standards du Volt et de la Seconde[3].
Effet Josephson continu
L'équation du paragraphe ci-dessus, liant le courant à la différence de tension appliquée à la jonction, peut particulièrement s'écrire à tension nulle. On obtient alors un courant continu Ic caractéristique de la jonction et nommé "courant critique". Dit autrement, une jonction soumise à une différence de tension nulle est le siège d'un courant continu de paires de Cooper.
L'effet Josephson continu s'observe fréquemment en appliquant un champ magnétique à une jonction Josephson. Le champ magnétique provoque un déphasage entre les paires de Cooper qui traversent la jonction d'une manière analogue à l'effet Aharonov-Bohm. Ce déphasage peut produire des interférences destructives entre les paires de Cooper, ce qui entraîne une réduction du courant maximal pouvant traverser la jonction. Si Φ est le flux magnétique à travers la jonction, on a la relation :
Les jonctions Josephson : un système à hautes performances
Les jonctions Josephson, par leur propriétés physiques, forment un système de choix pour plusieurs domaines d'application :
- C'est le constituant élémentaire du SQUID (Superconducting Quantum Interference Device), le plus fin détecteur de champ magnétique (et par conséquent de courant). Un SQUID est constitué de 2 jonctions en parallèles dans une boucle.
- C'est aussi le constituant de base de la logique rapide dite RSFQ (Rapid Single FLux Quantum) où elles jouent le rôle du transistor et autoriseraient des cadences en centaines de Ghz.
- C'est aussi un des détecteurs de photons les plus performants. On parle alors de jonctions supraconductrices à effet tunnel (STJ en anglais). Ces systèmes combinent une sensibilité ultime jusqu'aux photons uniques dans une large bande spectrale (des rayons X au proche infrarouge) avec une bonne résolution en énergie.
Note et références
- ↑ B. D. Josephson, Phys. Lett., 1, 251 (1962).
- ↑ Barone A, Paterno G. Physics and Applications of the Josephson Effect. New York : John Wiley & Sons; 1982.
- ↑ Laboratoire National de métrologie et d'essai : «Représentation du Volt par l'effet Josephson»
- (en) J. M. Ziman, Principles of the Theory of Solids, Cambridge University Press ;
- (en) M. Tinkham, Introduction to Superconductivity, McGraw-Hill ;
- (en) P. W. Anderson, Basic Notions of Condensed Matter Physics, Addison-Wesley.
Liens externes
- B. Dutoit : «EPFL : SQUIDs et effet Josephson» ;
- Laboratoire National de métrologie et d'essai : «Représentation du Volt par l'effet Josephson» ;
- Les jonctions comme détecteurs de photons : thèse de l'INPG, 2004
- (en) SQUID
- (en) RSFQ
- (en) Fondation Nobel : l'effet Josephson ;
- (en) HyperPhysics : magnétomètres SQUID.
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 12/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

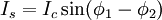
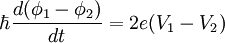
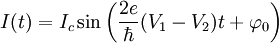
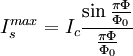

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité