Physique des polymères
Voir aussi Polymère.
Recherche sur Google Images :

Source image : recherche.enscpb.fr Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- La signification physique de ces maxima d'intensité et de viscosité réduite... relatif des deux chaînes de polymère dans le solvant et caractérise par conséquent... (source : recherche.enscpb)
- toutes les propriétés d'une chaîne dans un fondu polymère seraient semblables à celles présentes en solvant -Θ. C'est à dire, l'unique effet de la phase... (source : www-ics.u-strasbg)
- Bon solvant : le couple polymère - solvant est tel qu'un monomère minimise son.... Pour une chaîne polymère de N maillons de masse molaire m0 et de masse... (source : ilephysique)
Voir aussi Polymère.
La physique des polymères s'intéresse aux propriétés des matériaux constitués de longues molécules, assemblages en chaînes de dizaines de molécules élémentaires : les polymères. Ces molécules peuvent être observées à l'état solide, liquide, en solution ou confinées à une interface. Leurs propriétés physiques particulièrement spécifiques ont conduit au développement d'outils théoriques spécifiques ainsi qu'à la naissance de cette nouvelle branche de la physique aux applications nombreuses.
Polymères en solution
Les premiers éclairages théoriques importants concernant les polymères fondus ou en solution ont été apportés par la physique statistique. Du fait de la géométrie spécifique des molécules, on comprend actuellement mieux leurs propriétés que celle de certains liquides "simples" comme l'eau.
Polymères gaussiens
C'est le modèle physique décrivant les polymères le plus simple. On considère que chaque monomère a une longueur fixée a et est orienté de manière aléatoire, l'ensemble des directions étant équiprobables (matériau isotrope). Ainsi, la géométrie d'une chaîne est équivalente à celle d'une marche aléatoire simple à 3 dimensions. Dans ce cas, on peut montrer que pour la plupart de pas, la distance entre les deux extrémités de la chaîne suit une loi gaussienne, d'où le nom du modèle. Ce modèle néglige cependant l'ensemble des interactions entre monomères pouvant induire des corrélations entre les orientations.
L'organisation spatiale d'un polymère est particulièrement étendue. Comme dans une structure comme la tour Eiffel, une grande partie de l'espace est cependant vide (ou contient de l'air pour la tour Eiffel et du solvant pour un polymère). On peut malgré tout définir fonctionnellement et mathématiquement l'étendue spatiale occupée par un polymère à travers son rayon de giration. Mathématiquement, il s'agit de la distance moyenne entre une extrémité de la chaîne et le centre de masse de la structure. En mesurant les interactions hydrodynamiques entre le polymère et son solvant (en regardant par exemple comment le polymère diffuse dans le solvant), on peut évaluer expérimentalement son rayon de giration Rg.
Ceci conduit pour un polymère gaussien à :
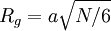
où N est le nombre total de monomères et a la taille (longueur de Kuhn) de chacun de ces monomères.
Polymères réels
En général, les interactions entre monomères proches dépendent de leur orientation relative et le modèle gaussien donne par conséquent de mauvais résultats. Les forces pouvant entrer en jeu sont :
- Les forces de Van der Waals
- Les forces de répulsion à courte portée entre atomes
- Les forces électrostatiques (cas de monomères chargés)
Les forces de Van der Waals et les forces électrostatiques dépendent fortement du solvant utilisé et de la température. Généralement, il existe une température, généralement notée θ, à laquelle les effets de ces interactions se compensent. On dit que le polymère est en bon solvant si T > θ. Quand T > > θ, les interactions attractives deviennent négligeables et on peut estimer le potentiel répulsif par un cœur dur.
Le comportement des polymères en bon solvant a été étudié originellement par Flory. Expérimentalement, on observe une dépendance du rayon de giration comparable à celle prédite par le modèle gaussien, mais corrigée par un exposant de Flory ν :
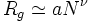 avec
avec 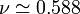
.
La valeur 0.588 est universelle (dans les conditions du bon solvant) et ne dépend que de la dimension de l'espace. A titre d'exemple, pour des polymères confinés sur une droite, on utilise par définition ν = 1. Par des méthodes statistiques poussées, on peut aussi montrer qu'en dimension deux : ν = 0.75. Les résultats modernes sur ce sujet sont liés à la théorie des marches aléatoires auto-évitantes.
Polymères greffés
On dit que des polymères sont greffés sur une surface quand l'une des extrémités de la chaîne y est tenue par une liaison chimique, le reste étant libre dans le solvant. Au-delà d'une certaine densité, les chaînes voisines vont se mettre à interagir de façon non isotrope. Les polymères sont alors étirés par l'encombrement. On montre que, si σ est la densité surfacique de polymères, l'épaisseur de la couche greffée vérifie alors la loi d'échelle :
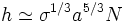
La présence d'une couche de polymères greffés crée un potentiel répulsif au voisinage de la surface. Ainsi, des suspensions colloïdales peuvent y être stabilisées.
Polymères biologiques
Il s'agit principalement de l'ADN, l'ARN et des protéines. Plusieurs caractéristiques importantes rendent leur étude différente.


 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité