Évaporation des trous noirs

Le rayonnement de Hawking est le phénomène selon lequel un observateur regardant un trou noir peut détecter un infime rayonnement de corps noir émanant de la surface de ce dernier.

Catégories :

Théorie quantique des champs - Physique quantique - Trou noir

Source image : www.techno-science.net
Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur.

Page(s) en rapport avec ce sujet :

terme un trou noir, il doit répondre à des critères de masse précis, .... d'évaporation des trous noirs est tout de même passablement lent et le trou noir... (source : astrospatiale.free)
Ainsi, le Trou noir est un «objet» stellaire qui reste toujours en mouvement d'expansion, et ne peut en aucun cas diminuer ni de volume, ni de masse, ... (source : july.fixedreference)
Lorsque on a fait deux ans de physique (et toujours), on sait que le trou noir attire tout grâce à son immense masse. Le trou noir au CERN va être créé (et oui, ... (source : korben)

Article principal : Trou noir.

Le rayonnement de Hawking est le phénomène selon lequel un observateur regardant un trou noir peut détecter un infime rayonnement de corps noir émanant de la surface de ce dernier. Ce phénomène est aussi nommé, pour des raisons évidentes, évaporation des trous noirs. Il a été prédit par Stephen Hawking en 1975^[1], et est reconnu comme l'une de ses plus importantes réalisations.

La découverte théorique de ce phénomène a donné une justification à une branche de l'étude des trous noirs nommée thermodynamique des trous noirs, développée peu avant la découverte de Hawking, et qui suggérait qu'il devait être envisageable d'associer une température à un trou noir. Cependant, au niveau classique, il était démontré qu'un trou noir ne pouvait émettre de rayonnement (c'est même, en quelque sorte, la définition d'un trou noir). Ce paradoxe a été résolu par Stephen Hawking, qui a démontré que des effets d'origine quantique étaient à l'origine d'un tel phénomène.

Le rayonnement de Hawking s'avère extragénéralement faible pour les trous noirs issus de l'évolution stellaire et toujours plus faible pour les autres trous noirs indirectement détectés dans l'univers (trous noirs intermédiaires et trous noirs supermassifs), aussi sa mise en évidence est-elle impossible à l'heure actuelle. Elle pourrait être rendue envisageable par l'existence de trous noirs de petite taille (microscopique). De tels objets pourraient avoir été produits lors du Big Bang (on parle de trous noirs essentiels), ou alors être produits dans des accélérateurs de particules dans le cadre de certaines théories au-delà du modèle standard de la physique des particules^[2].

Il existe un analogue cinématique au phénomène de rayonnement de Hawking, l'effet Unruh, du nom du physicien canadien William Unruh, qui l'a prédit en 1976. Ce dernier prédit qu'un observateur qui regarderait un miroir animé d'un mouvement accéléré aurait l'impression que ce dernier émet un rayonnement thermique, dont la température est proportionnelle à l'accélération du miroir. Dans un contexte légèrement différent, l'effet Schwinger, qui décrit la création de particules chargées dans un champ électrique, peut être vu comme un analogue électrostatique du rayonnement de Hawking.

Divers processus issus de la mécanique classique sont à ne pas à confondre avec l'effet Hawking, surtout ceux permettant d'extraire de l'énergie d'un trou noir : le processus de Penrose, ou son analogue ondulatoire, le superradiance ^[3]. De même, les phénomènes d'éjection de matière par l'intermédiaire de jets issus d'un disque d'accrétion entourant le trou noir n'ont strictement rien à voir avec le phénomène d'évaporation des trous noirs.

Le rayonnement de Hawking

La théorie quantique des champs (c'est-à-dire les lois de la mécanique quantique appliquée dans le cadre de la relativité restreinte) explique l'existence des fluctuations du vide : des paires particule-antiparticule sont en permanence générées par le vide. Des effets de ces fluctuations du vide peuvent être mis en évidence par divers phénomènes, comme l'effet Casimir en physique des particules, ou le déplacement de Lamb dans le spectre des niveaux d'énergie d'un électron dans un atome d'hydrogène.

De façon générale, ces paires de particules-antiparticules s'annihilent aussitôt, sauf si un phénomène physique permet de les séparer les unes des autres en un temps inférieur à la durée de vie typique de la paire. Dans le cas de l'effet Hawking, à l'horizon d'un trou noir, les forces de marée générées par le champ gravitationnel du trou noir sont si intenses qu'elles peuvent éloigner la particule de son antiparticule, avant qu'elles ne s'annihilent. L'une est absorbée par le trou noir, alors que l'autre (la particule émise) s'en éloigne dans un sens opposé. De façon heuristique, l'énergie de la paire particule anti-particule, mesurée par un observateur localisé loin du trou noir est négative, du fait que les deux particules sont piégées dans le puits de potentiel du trou noir. De façon schématique, il est envisageable que la répartition d'énergie au sein de la paire particule anti-particule donne à l'une des deux une énergie qui serait reconnue comme positive par un observateur distant, c'est-à-dire lui servant à s'échapper de son champ gravitationnel. Dans un tel cas, l'absorption de l'autre particule peut être vue comme l'absorption d'une particule d'énergie négative, produisant une diminution de sa masse. L'énergie des particules émises augmente avec la température du trou noir. En dessous d'une température limite, l'émission ne se fait qu'avec des particules de masse nulle comme les photons ou les gravitons et peut-être les neutrinos. Au dessus, l'émission de tous types de particules est envisageable, bien que ce régime ne concerne que la toute fin de l'évolution des trous noirs. Au cours du plus gros de leur existence, ceux-ci rayonnent des particules sans masse (voir ci-dessous).

Formules et ordres de grandeur

Un calcul célèbre ayant donné naissance à ce qu'on nomme la thermodynamique des trous noirs sert à montrer qu'on peut exprimer la masse M d'un trou noir selon sa taille (en fait la surface A de son horizon), et des autres paramètres macroscopiques le caractérisant, à savoir, pour un trou noir de type astrophysique, sa charge électrique Q et son moment cinétique L. Il existe par conséquent une fonction de la forme

M = M (A, Q, L)

La quantité 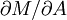$\partial M / \partial A$ peut s'écrire sous la forme

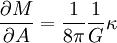$\frac{\partial M}{\partial A} = \frac{1}{8 \pi} \frac{1}{G} \kappa$ ,

où G est la constante de Newton et κ est une quantité nommée gravité de surface du trou noir, et qui détermine à quelle vitesse le champ gravitationnel d'un trou noir diverge à mesure qu'on s'approche de l'horizon. Les calculs de Hawking sur l'évaporation des trous noirs indiquent que la température T qui peut leur être associée est donnée par

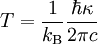$T = \frac{1}{k_{\mathrm{B}}} \frac{\hbar \kappa}{2 \pi c}$ ,

où k_B est la constante de Boltzmann, c est la vitesse de la lumière et 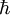$\hbar$ la constante de Planck réduite. Cette température est aussi nommée température de Hawking. Ceci justifie a priori la totalité des calculs sur la thermodynamique des trous noirs : en effet, la différentielle de la masse selon l'aire des des autres quantités s'identifie à la formule du premier principe de la thermodynamique,

d U = T d S +...

où l'énergie interne U est remplacée dans le cas des trous noirs par leur masse (représentant leur énergie totale), et l'entropie S est , selon les calculs de la thermodynamique des trous noirs, proportionnelle à la surface A de leur horizon. Pour rendre la totalité de la thermodynamique des trous noirs cohérente, il fallait démontrer que les trous noirs pouvaient posséder une température proportionnelle à la gravité de surface, ce qui a été réalisé par Hawking.

Cas d'un trou noir de Schwarzschild

Dans le cas d'un trou noir de Schwarzschild, on a une relation simple entre la masse et la surface du trou noir : le rayon de Schwarzschild R s'écrit

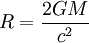$R = \frac{2 G M}{cˆ2}$ ,

et sa surface ( $A = 4π R 2$ pour une sphère)

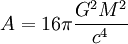$A = 16 \pi \frac{Gˆ2 Mˆ2}{cˆ4}$ .

On peut alors exprimer M selon A de la manière suivante

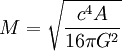$M = \sqrt{\frac{cˆ4 A}{16 \pi Gˆ2}}$ .

On a donc

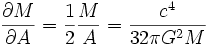$\frac{\partial M}{\partial A} = \frac{1}{2} \frac{M}{A} = \frac{cˆ4}{32 \pi Gˆ2 M}$ ,

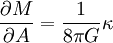$\frac{\partial M}{\partial A} = \frac{1}{8 \pi G} \kappa$ .

La gravité de surface est donc

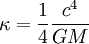$\kappa = \frac{1}{4} \frac{cˆ4}{G M}$ ,

incidemment en accord avec la formule usuelle $κ = G M / R 2$ , et la température vaut

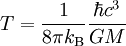$T = \frac{1}{8 \pi k_{\mathrm{B}}} \frac{\hbar cˆ3}{G M}$ .

La température est par conséquent inversement proportionnelle à la masse. Ce résultat n'est guère étonnant : l'unique échelle de longueur du problème est le rayon de Schwarzschild, proportionnelle à la masse. La température d'un rayonnement est déterminée par l'énergie typique des particules (en l'occurrence des photons), de fréquence ν, selon une formule du type 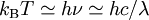$k_{\mathrm{B}} T \simeq h \nu \simeq h c / \lambda$ . Il est naturel que la longueur d'onde des photons soit déterminée par l'échelle de longueur disponible, proportionnelle à la masse, aussi la température est-elle naturellement inversement proportionnelle à cette dernière.

La formule précédente peut se réécrire en unités de Planck selon

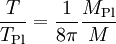$\frac{T}{T_{\mathrm{Pl}}} = \frac{1}{8 \pi} \frac{M_{\mathrm{Pl}}}{M}$ .

De façon plus intéressante, on peut la réécrire en unité de masse solaire, ce qui donne :

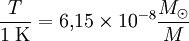$\frac{T}{1\;{\mathrm{K}}} = 6,\!15 \times 10ˆ{-8} \frac{M_\odot}{M}$ .

Ainsi, un trou noir d'une masse solaire a une température de l'ordre du dix millionième de kelvin. Cette température augmente à mesure que la masse du trou noir diminue. Il existe par conséquent un effet d'emballement : plus le trou noir rayonne, plus il perd de l'énergie (sa masse va diminuer, voir ci-dessous), et plus il est chaud. Ceci n'est pas sans rappeler l'évolution stellaire, où une étoile est le siège de réactions nucléaires de plus en plus rapides à mesure que son évolution se poursuit.

Si cet ordre de grandeur est correct généralement, il est significativement erroné dans plusieurs cas. Surtout, pour un trou noir extrémal, c'est-à-dire possédant une valeur maximale de la charge électrique ou du moment cinétique, alors on montre que la température du trou noir est strictement nulle. Un tel résultat est l'analogue en thermodynamique des trous noirs du troisième principe de la thermodynamique, qui indique qu'il n'est pas envisageable d'atteindre un état de température nulle (ou d'entropie minimale) par un quelconque processus physique.

Évolution d'un trou noir isolé

Une autre conséquence de la dépendance inverse entre température et masse est qu'un trou noir ne peut pas être en équilibre avec un bain thermique : si la température du bain est supérieure à celle du trou noir, le trou noir va plus absorber de rayonnement qu'il ne va en émettre, et ainsi augmenter sa masse et diminuer sa température. L'écart de température entre le trou noir et le bain thermique va par conséquent augmenter. Il en est de même si cette fois la température du bain est inférieure à celle du trou noir. Cette fois, c'est la température du trou noir qui va augmenter et différer de plus en plus de celle du bain.

À l'heure actuelle, l'univers entier baigne dans un rayonnement thermique, le fond diffus cosmologique. Ce rayonnement est à une température de 2, 7 kelvins, qui est par conséquent supérieure à celle d'un trou noir stellaire. Un tel trou noir, même s'il est totalement isolé (pas d'accrétion de matière du milieu interstellaire ou d'un compagnon), va par conséquent absorber du rayonnement. Cette phase va durer jusqu'à ce que la température du fond diffus cosmologique ait suffisamment baissé du fait de l'expansion de l'univers. La durée de cette phase peut être calculée de façon approximative en utilisant les paramètres issus du modèle standard de la cosmologie. À l'heure actuelle, on assiste à une accélération de l'expansion de l'univers, qui se traduit par le fait que l'expansion semble tendre vers une loi exponentielle, où les distances sont multipliées par 2, 7 en un temps de l'ordre du temps de Hubble, soit 13, 5 milliards d'années. La température du fond diffus cosmologique décroît comme l'inverse de la dilatation des longueurs. Ainsi, pour que la température du fond diffus cosmologique atteigne la valeur de 6, 15×10^-8 K, il faut attendre à peu près 18 temps de Hubble^[4]. Des trous noirs moins massifs que des trous noirs stellaires pourraient, eux, être en train de s'évaporer actuellement. Pour cela, il faut que leur masse soit inférieure à

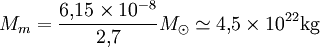$M_m = \frac{6,\!15\times 10ˆ{-8}}{2,\!7} M_\odot \simeq 4,\!5 \times 10ˆ{22} {\mathrm{kg}}$ ,

soit une masse comprise entre celles de Mercure et Pluton.

Aucun processus astrophysique connu ne sert à réaliser des trous noirs de masse aussi petite, mais il est envisageable que de tels objets se soient constitués dans l'univers essentiel. De tels trous noirs essentiels pourraient exister, et révéler leur signature par le phénomène d'évaporation. En effet, en fin d'évaporation, tandis que le trou noir atteint une masse de quelques milliards de tonnes uniquement, un trou noir rayonne à une température de l'ordre de 10¹¹ K, soit dans le domaine des rayons gamma, et pourrait laisser une signature observationnelle dans ce domaine de longueur d'onde^[5].

Temps d'évaporation

Il est envisageable d'estimer (avec des incertitudes, voir ci-dessous) le temps d'évaporation d'un trou noir. D'ordinaire, l'énergie rayonnée par un corps sphérique dont la température de surface est T et le rayon est R s'écrit

L = 4π R 2 σ T 4

où σ est la constante de Stefan-Boltzmann. La perte d'énergie de masse d'un trou noir s'écrit par conséquent en théorie

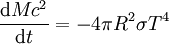$\frac{{\mathrm{d}} M cˆ2}{{\mathrm{d}} t} = - 4 \pi Rˆ2 \sigma Tˆ4$ .

Pour un trou noir de Schwarzschild, ceci s'écrit

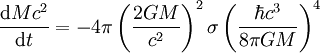$\frac{{\mathrm{d}} M cˆ2}{{\mathrm{d}} t} = - 4 \pi \left(\frac{2 G M}{cˆ2} \right)ˆ2 \sigma \left(\frac{\hbar cˆ3}{8 \pi G M}\right)ˆ4$ ,

soit, en remplaçant la constante de Stefan-Boltzmann par sa valeur,

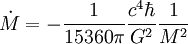$\dot M = - \frac{1}{15360 \pi} \frac{cˆ4 \hbar}{Gˆ2} \frac{1}{Mˆ2}$ .

Le temps d'évaporation d'un trou noir de masse M s'écrit donc

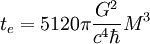$t_e = 5120 \pi \frac{Gˆ2}{cˆ4 \hbar} Mˆ3$ .

En unités de masses solaires, on obtient

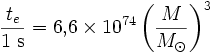$\frac{t_e}{1\;{\mathrm{s}}} = 6,\!6 \times 10ˆ{74} \left(\frac{M}{M_\odot}\right)ˆ3$ .

Une telle durée est à peu près 10⁵⁷ fois plus grande que l'âge de l'univers, illustrant le fait que l'évaporation de trous noirs stellaires est complètement négligeable. Par contre, des objets de masse 10¹⁹ fois plus faible qu'une masse solaire, soit de l'ordre d'un milliard de tonnes, ont un temps d'évaporation inférieur à l'âge de l'univers. Si de tels objets ont été produits lors du Big Bang, alors leur évaporation a lieu actuellement.

Limites du calcul du temps d'évaporation

Si la dérivation ci-dessus est globalement correcte, elle comporte un certain nombre d'approximations qui la rendent incorrecte. Surtout, la première équation (qui donne la perte d'énergie selon la surface d'émission) s'avère incorrecte, car la quantité qui devrait intervenir n'est pas la surface, mais la section efficace d'un trou noir. D'ordinaire, ces deux quantités sont semblable à un facteur 4 près (la surface vaut 4 π R² et la section efficace π R²). Cependant, dans le cas d'un trou noir, la taille angulaire d'un trou noir est plus grande d'un facteur 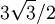$3 \sqrt{3} / 2$ que ce qu'un calcul naïf donnerait. Ainsi, au lieu de l'aire du trou noir dans la formule ci-dessus, il faudrait rajouter un facteur 27/4.

De plus, ce type de calcul est fait dans l'approximation de l'optique géométrique, où on suppose que les photons peuvent être assimilés à des particules ponctuelles, ou en tout cas de dimensions toujours particulièrement petites devant les autres dimensions du problème. Or dans le cas de l'évaporation des trous noirs, la longueur d'onde des photons est du même ordre que la taille physique du trou noir. Il conviendrait par conséquent de se placer dans les calculs dans le cadre de l'optique physique, où serait prise en compte la forme exacte du front d'onde dans le champ gravitationnel du trou noir.

Enfin, il a été supposé ici que le trou noir émet seulement des photons. En pratique, le phénomène d'évaporation concerne l'ensemble des particules existantes, en tout cas toutes celles dont l'énergie de masse est inférieure à l'énergie typique des particules du rayonnement. En pratique, le trou noir rayonne aussi des gravitons, ou alors des neutrinos (si leur masse est suffisamment faible) en plus des photons. Vers la fin de sa vie, lorsque sa température atteint le domaine du gigaélectronvolt, il peut rayonner des quarks, des muons ou alors d'autres particules pour l'heure inconnues. Cependant, ces dernières étapes ne concernent la toute fin de l'évolution du trou noir. Les premiers calculs détaillés du taux d'évaporation ont été effectués par Don Page en 1976^[6].

Au final, ces effets ne sont pas censés affecter le résultat général, mais pourraient le corriger d'un facteur numérique qui pourrait être fort différent de 1, mais il apparait peu probable qu'il s'éloigne de façon exorbitante de 1. Aussi, le fait qu'un trou noir de masse stellaire ne puisse pas s'évaporer en un temps inférieur à l'âge de l'Univers est-il un résultat extrêmement robuste.

Trous noirs et information

Article détaillé : Théorème de calvitie.

Le théorème no hair (de calvitie) qui décrit que seuls trois paramètres macroscopiques définissent l'état d'un trou noir pose un problème aux yeux de la théorie quantique. Si on envoie dans un trou noir un ensemble dit pur de particules, c'est-à-dire un faisceau cohérent (par exemple, un rayon laser, une paire de Cooper), le retour de cette énergie cohérente se fait sous la forme d'une énergie incohérente, une radiation thermique, un ensemble dit mixte. Or, les fonctions d'ondes qui décrivent ces deux types d'ensembles sont différents : dans le cas de la totalité pur les fonctions d'ondes s'additionnent vectoriellement, dans le cas d'un ensemble mixte, ce sont les carrés des modules des fonctions d'ondes qui s'additionnent. La transformation d'un ensemble en un autre n'est pas envisageable au sens quantique, dans la mesure où il ne s'agit pas d'une transformation unitaire (qui préserve la norme de la fonction d'onde).

D'où problème. Stephen Hawking a annoncé avoir résolu ce paradoxe, mais les détails de sa solution ne sont pas toujours (02/2005) connus.

Liens externes

(en) Observation of negative-frequency waves in a water tank : a classical analogue to the Hawking effect?, Germain Rousseau et al. Article du New journal of physic.

Références

(en) Robert M. Wald, General Relativity, University of Chicago Press, 1984, 498 pages (ISBN 0226870332) , pages 412 à 414.

Notes

↑ (en) S. W. Hawking, Particle Creation by Black Holes, Communications in Mathematical Physics , 43, 199-220 (1975) ; Erratum ibid. , 46, 206 (1976) Voir en ligne.
↑ Voir par exemple (en) Panagiota Kanti, Black Holes in Theories with Large Extra Dimensions : a Review, Mondial Journal of Modern Physics , A19, 4899-4951 (2004), hep-ph/0402168 Voir en ligne ; ou (en) Aurélien Barrau & J. Grain, Gauss-Bonnet Black Holes at the LHC : Beyond the Dimensionality of Space, Physics Letters B , 584, 114 (2004), hep-ph/0311238 Voir en ligne.
↑ Il est en effet envisageable d'extraire de l'énergie d'un trou noir : la masse d'un trou noir, qu'on mesure par son champ gravitationnel à longue distance est composée pour partie de diverses formes d'énergie, comme de l'énergie électrostatique, qui peuvent être récupérées, par exemple en diminuant la charge électrique d'un trou noir en lui injectant des particules de charge opposées et de masse négligeable. L'autre partie de la masse, nommée masse irréductible, ne peut, elle , être extraite du trou noir. Pour tout trou noir, la masse est toujours supérieure ou identique à la masse irréductible, et leur différence peut être récupérée par divers processus comme ceux précités.
↑ Ce chiffre se calcule simplement par la formule

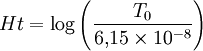$H t = \log\left(\frac{T_0}{6,\!15\times 10ˆ{-8}}\right)$ ,

T₀ étant la température actuelle du fond diffus cosmologique et H la constante de Hubble. Ceci résulte du fait que dans l'hypothèse où l'expansion est exponentielle, la température fluctue selon

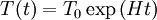$T (t) = T_0 \exp\left(H t\right)$ ,

en prenant l'origine des temps actuellement.
↑ Voir par exemple (en) Aurélien Barrau et al. , Antiprotons from essentiel black holes, Astronomy and Astrophysics, 388, 676 (2002), astro-ph/0112486 Voir en ligne ; (en) Aurélien Barrau et al. , Antideuterons as a probe of essentiel black holes, Astronomy and Astrophysics, 398, 403 (2003), astro-ph/0207395 Voir en ligne ; (en) Aurélien Barrau et al. , Astrophysical Production of Microscopic Black Holes in a Low Planck-scale World, Astrophysical Journal, 630, 1015 (2005), astro-ph/0505436 Voir en ligne.
↑ (en) Don Page, Particle emission rates from a black hole : Massless particles from an uncharged, nonrotating hole, Physical Review D, 13, 198-206 (1976) Voir en ligne (accès restreint) .

Recherche sur Amazone (livres) :

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/%C3%89vaporation_des_trous_noirs.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 12/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.