Lentille magnétique
Une lentille magnétique est un système produisant un champ magnétique à symétrie de révolution, utilisé dans des appareils comme les microscopes électroniques pour focaliser les faisceaux d'électrons de la même façon que les lentilles en verre...
Recherche sur Google Images :
Source image : serveurweb.lps.u-psud.fr Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- magnétiques remplaçant les lentilles minces en verre, pour former l'image de l'objet. Une lentille magnétique est constituée par un champ magnétique non... (source : thierry.chave.free)
- Montrer que le champ magnétique B (M) créé par la spire s'écrit sous... B. IILS. b Le référentiel du laboratoire, où la lentille magnétique est fixe... (source : capes-pc.univ-pau)
- profondeur de champ réduite peut-être taille de l'échantillon limitée... (la rotation des trajectoires dans la lentille magnétique est ... (source : cimeepfl)
Une lentille magnétique est un système produisant un champ magnétique à symétrie de révolution, utilisé dans des appareils comme les microscopes électroniques pour focaliser les faisceaux d'électrons de la même façon que les lentilles en verre sont utilisées dans les appareils d'optique photonique.
Description du système
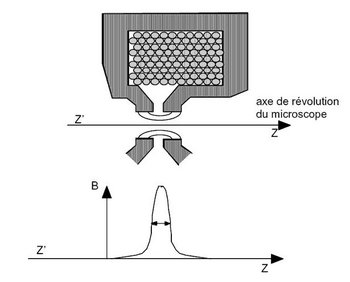
Ce sont les composantes radiales du champ magnétiques qui vont communiquer à un électron en mouvement sur une trajectoire parallèle à l'axe une vitesse azimutale. Une fois la vitesse azimutale créée, on comprend quoique le champ magnétique axial exercera une force radiale faisant ainsi converger la trajectoire vers l'axe.
Distance focale
Approximation lentilles minces :
où :
- e est la charge de l'électron
- m0 est la masse de l'électron
- U0 est le potentiel d'accelération des électrons
- Bz est la composante axiale du champ magnétique
Rotation induite par la lentille
Aberration chromatique
où f est la focale dont l'expression est donnée ci-dessus
Aberration sphérique
Il n'y a pas de formule simple de l'aberration sphérique. Schertzer a établi un théorème selon lequel l'aberration sphérique est toujours positive
Historique
Depuis la fin du XIXe siècle, le tube à rayons cathodiques a cessé d'être un pur objet de laboratoire pour devenir un système qu'on cherche à perfectionner pour des raisons pratiques. Le nom de Ferdinand Braun est attaché aux premiers développements des tubes cathodiques. Dans les années 1920, les recherches appliquées se précisent, en direction de l'oscilloscope et légèrement plus tard, de la télévision.
C'est dans ce contexte que se situe, en 1924-26, le sujet de la thèse de Dennis Gabor, un Hongrois qui travaille à l'institut d'électrotechnique de la Technischen Hochschule de Berlin. Depuis longtemps, on avait remarqué qu'un champ magnétique créé avec une bobine dans l'axe du faisceau avait tendance à concentrer plus ou moins le faisceau. Pour pouvoir disposer des plaques de déflexion après la concentration du faisceau, Gabor fut amené à restreindre la présence du champ magnétique sur une courte longueur grâce à des pièces magnétiques à symétrie de révolution qui canalisaient le champ sur la région utile. Les résultats furent suffisamment bons pour que l'un de ses collègues, Hans Busch, entreprit de retrouver par le calcul l'effet de concentration subi par les trajectoires. Ses équations le conduisirent ainsi à une relation équivalente à la célèbre formule des lentilles minces
La maîtrise des lentilles magnétiques aura une grande importance dans le développement, dans le même laboratoire, du premier microscope électronique, qui valut le prix Nobel à Ernst Ruska.
- Sur l'optique électronique : (en) P. W. Hawkes & Kasper, Principles of Electron Optics, Academic Press, 1989
- Sur l'histoire : (en) Ernst Ruska, the early developments of electron microscopy, Hirzel, 1980, IBSN 3777603643
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

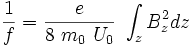
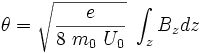
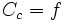

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité